Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T02:34:06.608Z Has data issue: false hasContentIssue false
  • English
  • Français

ENCOMPASSING TESTS FOR NONPARAMETRIC REGRESSIONS

Published online by Cambridge University Press:  17 April 2024

Elia Lapenta  and
Pascal Lavergne Open the ORCID record for Pascal Lavergne [Opens in a new window]
Elia Lapenta*
Affiliation:
CREST and ENSAE, Institut Polytechnique de Paris
Pascal Lavergne
Affiliation:
Toulouse School of Economics, Université Toulouse Capitole
*
Address correspondence to Elia Lapenta, CREST, 5 Avenue Le Chatelier, 91120 Palaiseau, France; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We set up a formal framework to characterize encompassing of nonparametric models through the 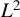$L^2$ distance. We contrast it to previous literature on the comparison of nonparametric regression models. We then develop testing procedures for the encompassing hypothesis that are fully nonparametric. Our test statistics depend on kernel regression, raising the issue of bandwidth’s choice. We investigate two alternative approaches to obtain a “small bias property” for our test statistics. We show the validity of a wild bootstrap method. We empirically study the use of a data-driven bandwidth and illustrate the attractive features of our tests for small and moderate samples.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 30
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Footnotes

We thank the co-editor Michael Jansson and two referees for their comments that helped to improve the paper significantly. Elia Lapenta acknowledges funding from the French National Research Agency (ANR) under grant ANR-23-CE26-0008-01. Pascal Lavergne acknowledges funding from ANR under grant ANR-17-EURE-0010 (Investissements d’Avenir program).

References

REFERENCES

Ait-Sahalia, Y., Bickel, P. J., & Stoker, T. M. (2001). Goodness-of-fit tests for kernel regression with an application to option implied volatilities. Journal of Econometrics, 105, 363–412.CrossRefGoogle Scholar
Andrews, D. W. K. (1994). Empirical process methods in econometrics. In R.F. Engle and D.L. McFadden (eds), Handbook of Econometrics (pp. 2247–2294), vol. 4. Elsevier.Google Scholar
Andrews, D. W. K. (1995). Nonparametric kernel estimation for semiparametric models. Econometric Theory, 11, 560–586.CrossRefGoogle Scholar
Arellano, M., Blundell, R., & Bonhomme, S. (2017). Earnings and consumption dynamics: A nonlinear panel data framework. Econometrica, 85, 693–734.CrossRefGoogle Scholar
Bentkus, V., Götze, F., & Zitikis, R. (1993). Asymptotic expansions in the integral and local limit theorems in Banach spaces with applications to $w$ -statistics. Journal of Theoretical Probability, 6,54.CrossRefGoogle Scholar
Bierens, H. J. (1982). Consistent model specification tests. Journal of Econometrics, 20, 105–134.CrossRefGoogle Scholar
Bierens, H. J. (1990). A consistent conditional moment test of functional form. Econometrica, 58, 1443–1458.CrossRefGoogle Scholar
Bierens, H. J. (2017). Econometric model specification. World Scientific.CrossRefGoogle Scholar
Bierens, H. J., & Ploberger, W. (1997). Asymptotic theory of integrated conditional moment tests. Econometrica, 65, 1129–1152.CrossRefGoogle Scholar
Bontemps, C., Florens, J.-P., & Richard, J.-F. (2008). Parametric and non-parametric encompassing procedures. Oxford Bulletin of Economics and Statistics, 70, 751–780.CrossRefGoogle Scholar
Bontemps, C., & Mizon, G. E. (2008). Encompassing: Concepts and implementation. Oxford Bulletin of Economics and Statistics, 70, 721–750.CrossRefGoogle Scholar
Chernozhukov, V., Escanciano, J. C., Ichimura, H., Newey, W. K., & Robins, J. M. (2022). Locally robust semiparametric estimation. Econometrica, 90, 1501–1535.CrossRefGoogle Scholar
Davidson, R., & MacKinnon, J. G. (2007). Improving the reliability of bootstrap tests with the fast double bootstrap. Computational Statistics & Data Analysis, 51, 3259–3281.CrossRefGoogle Scholar
Delgado, M. A., & Manteiga, W. G. (2001). Significance testing in nonparametric regression based on the bootstrap. Annals of Statistics, 29, 1469–1507.CrossRefGoogle Scholar
Delgado, M. A., & Stute, W. (2008). Distribution-free specification tests of conditional models. Journal of Econometrics, 143, 37–55.CrossRefGoogle Scholar
Dhaene, G., Gourieroux, C., & Scaillet, O. (1998). Instrumental models and indirect encompassing. Econometrica, 66, 673–688.CrossRefGoogle Scholar
Di Marzio, M., & Taylor, C. C. (2008). On boosting kernel regression. Journal of Statistical Planning and Inference, 138, 2483–2498.CrossRefGoogle Scholar
Escanciano, J. C. (2006). A consistent diagnostic test for regression models using projections. Econometric Theory, 22, 1030–1051.CrossRefGoogle Scholar
Escanciano, J. C., Jacho-Chávez, D. T., & Lewbel, A. (2014). Uniform convergence of weighted sums of non and semiparametric residuals for estimation and testing. Journal of Econometrics, 178, 426–443.CrossRefGoogle Scholar
Fan, Y., & Li, Q. (1996). Consistent model specification tests: Omitted variables and semiparametric functional forms. Econometrica, 64, 865–890.CrossRefGoogle Scholar
Florens, J.-P., Hendry, D. F., & Richard, J.-F. (1996). Encompassing and specificity. Econometric Theory, 12, 620–656.CrossRefGoogle Scholar
Gaver, K. M., & Geisel, M. S. (1974). Discriminating among alternative models: Bayesian and non-Bayesian methods. In Zarembka, P. (Ed.), Frontiers of econometrics (p. 80), 19. Academic Press.Google Scholar
Giacomini, R., Politis, D. N., & White, H. (2013). A warp-speed method for conducting Monte Carlo experiments involving bootstrap estimators. Econometric Theory, 29, 567–589.CrossRefGoogle Scholar
Gourieroux, C., & Monfort, A. (1995). Testing, encompassing, and simulating dynamic econometric models. Econometric Theory, 11, 195–228.CrossRefGoogle Scholar
Gourieroux, C., Monfort, A., & Trognon, A. (1983). Testing nested or non-nested hypotheses. Journal of Econometrics, 21, 83–115.CrossRefGoogle Scholar
Greene, W. H. (2003). Econometric analysis. (5th ed.) Prentice Hall.Google Scholar
Hendry, D. F., & Richard, J.-F. (1982). On the formulation of empirical models in dynamic econometrics. Journal of Econometrics, 20, 3–33.CrossRefGoogle Scholar
Hurvich, C. M., Simonoff, J. S., & Tsai, C.-L. (1998). Smoothing parameter selection in nonparametric regression using an improved Akaike information criterion. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 60, 271–293.CrossRefGoogle Scholar
Kosorok, M. R. (2008). Introduction to empirical processes and semiparametric inference. Springer.CrossRefGoogle Scholar
Lavergne, P. (2001). An equality test across nonparametric regressions. Journal of Econometrics, 103, 307–344.CrossRefGoogle Scholar
Lavergne, P., Maistre, S., & Patilea, V. (2015). A significance test for covariates in nonparametric regression. Electronic Journal of Statistics, 9, 643–678.CrossRefGoogle Scholar
Lavergne, P., & Patilea, V. (2008). Breaking the curse of dimensionality in nonparametric testing. Journal of Econometrics, 143, 103–122.CrossRefGoogle Scholar
Lavergne, P., & Vuong, Q. H. (1996). Nonparametric selection of regressors: The nonnested case. Econometrica, 64, 207–219.CrossRefGoogle Scholar
Lavergne, P., & Vuong, Q. H. (2000). Nonparametric significance testing. Econometric Theory, 16, 576–601.CrossRefGoogle Scholar
Li, Q., & Racine, J. (2004). Cross-validated local linear nonparametric regression. Statistica Sinica, 14, 485–512.Google Scholar
Li, Q., & Racine, J. S. (2006). Nonparametric econometrics: Theory and practice. Princeton University Press.Google Scholar
Liao, Z., & Shi, X. (2020). A nondegenerate Vuong test and post selection confidence intervals for semi/nonparametric models. Quantitative Economics, 11, 983–1017.CrossRefGoogle Scholar
Mammen, E. (1992). When does bootstrap work?. Lecture Notes in Statistics. Springer.CrossRefGoogle Scholar
Mammen, E., Rothe, C., & Schienle, M. (2016). Semiparametric estimation with generated covariates. Econometric Theory, 32, 1140–1177.CrossRefGoogle Scholar
Mizon, G. E., & Richard, J.-F. (1986). The encompassing principle and its application to testing non-nested hypotheses. Econometrica, 54, 657–678.CrossRefGoogle Scholar
Newey, W. K. (1990). Semiparametric efficiency bounds. Journal of Applied Econometrics, 5, 99–135.CrossRefGoogle Scholar
Newey, W. K., Hsieh, F., & Robins, J. M. (2004). Twicing kernels and a small bias property of semiparametric estimators. Econometrica, 72, 947–962.CrossRefGoogle Scholar
Park, B. U., Lee, Y. K., & Ha, S. (2009). L2 boosting in kernel regression. Bernoulli, 15, 599–613.CrossRefGoogle Scholar
Stinchcombe, M. B., & White, H. (1998). Consistent specification testing with nuisance parameters present only under the alternative. Econometric Theory, 14, 295–325.CrossRefGoogle Scholar
van der Vaart, A. W. (1998). Asymptotic statistics, Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press.CrossRefGoogle Scholar
van der Vaart, A. W., & Wellner, J. A. (2000). Weak convergence and empirical processes: With applications to statistics. Springer.Google Scholar
Xia, Y., Li, W. K., Tong, H., & Zhang, D. (2004). A goodness-of-fit test for single-index models. Statistica Sinica, 14, 1–28.Google Scholar
Supplementary material: File

Lapenta and Lavergne supplementary material

Lapenta and Lavergne supplementary material
Download Lapenta and Lavergne supplementary material(File)
File 183.4 KB