Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T18:17:59.323Z Has data issue: false hasContentIssue false
  • English
  • Français

EFFICIENT TWO-STEP GENERALIZED EMPIRICAL LIKELIHOOD ESTIMATION AND TESTS WITH MARTINGALE DIFFERENCES

Published online by Cambridge University Press:  29 June 2020

Fei Jin  and
Lung-fei Lee
Fei Jin
Affiliation:
Fudan University and Shanghai Institute of International Finance and Economics
Lung-fei Lee*
Affiliation:
The Ohio State University
*
Address correspondence to Lung-fei Lee, Department of Economics, The Ohio State University, Columbus, OH43210, USA; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers two-step generalized empirical likelihood (GEL) estimation and tests with martingale differences when there is a computationally simple 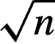$\sqrt n$-consistent estimator of nuisance parameters or the nuisance parameters can be eliminated with an estimating function of parameters of interest. As an initial estimate might have asymptotic impact on final estimates, we propose general 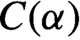$C(\alpha )$-type transformed moments to eliminate the impact, and use them in the GEL framework to construct estimation and tests robust to initial estimates. This two-step approach can save computational burden as the numbers of moments and parameters are reduced. A properly constructed two-step GEL (TGEL) estimator of parameters of interest is asymptotically as efficient as the corresponding joint GEL estimator. TGEL removes several higher-order bias terms of a corresponding two-step generalized method of moments. Our moment functions at the true parameters are martingales, thus they cover some spatial and time series models. We investigate tests for parameter restrictions in the TGEL framework, which are locally as powerful as those in the joint GEL framework when the two-step estimator is efficient.

Type
ARTICLES
Information
Econometric Theory , Volume 37 , Issue 3 , June 2021 , pp. 573 - 612
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

We are grateful to Co-Editor Patrik Guggenberger and three anonymous referees for their valuable suggestions and comments. Some of issues on testing of hypotheses using a GMM approach with an initial consistent estimate in a two-step estimation framework were posed by Professor Junsen Zhang of the Chinese University of Hong Kong. We appreciate Junsen for bringing some of the testing issues addressed in this paper to our attention. This paper has been presented at SMU and in the Third Guangzhou Econometrics Workshop at the Sun Yat-Sen University, Guangzhou, China. We are grateful to Zhentao Shi, Liangjun Su, Zhenlin Yang, Jun Yu, and other seminar participants for helpful comments. The first author gratefully acknowledges the financial support from the National Natural Science Foundation of China (Nos. 71973030 and 71833004) and Program for Innovative Research Team of Shanghai University of Finance and Economics.

References

Ackerberg, D., Chen, X., Hahn, J., & Liao, Z. (2014) Asymptotic efficiency of semiparametric two-step GMM. Review of Economic Studies 81(3), 919–943.CrossRefGoogle Scholar
Altonji, J.G. & Segal, L.M. (1996) Small-sample bias in GMM estimation of covariance structures. Journal of Business & Economic Statistics 14(3), 353–366.Google Scholar
Anatolyev, S. (2005) GMM, GEL, serial correlation, and asymptotic bias. Econometrica 73(3), 983–1002.CrossRefGoogle Scholar
Barro, R.J. (1977) Unanticipated money growth and unemployment in the United States. American Economic Review 67(2), 101–115.Google Scholar
Cattaneo, M.D., Jansson, M., & Ma, X. (2018) Two-step estimation and inference with possible many included covariates. Review of Economic Studies 86(3), 1095–1122.CrossRefGoogle Scholar
Chen, S.X. (1994) Empirical likelihood confidence intervals for linear regression coefficients. Journal of Multivariate Analysis 49(1), 24–40.CrossRefGoogle Scholar
Chen, S.X. & Cui, H. (2006) On Bartlett correction of empirical likelihood in the presence of nuisance parameters. Biometrika 93(1), 215–220.CrossRefGoogle Scholar
Chen, S.X. & Cui, H. (2007) On the second-order properties of empirical likelihood with moment restrictions. Journal of Econometrics 141, 492–516.CrossRefGoogle Scholar
Chernozhukov, V., Chetverikov, D., Demirer, M., Duflo, E., Hansen, C., Newey, W., & Robins, J. (2018a) Double/debiased machine learning for treatment and structural parameters. Econometrics Journal 21(1), C1–C68.CrossRefGoogle Scholar
Chernozhukov, V., Escanciano, J.C., Ichimura, H., Newey, W.K., & Robins, J.R. (2018b) Locally Robust Semiparametric Estimation. Working Paper.Google Scholar
Chuang, C.-S. & Chan, N.H. (2002) Empirical likelihood for autoregressive models, with applications to unstable time series. Statistical Sinica 12, 387–407.Google Scholar
Corcoran, S.A. (1998) Bartlett adjustment of empirical discrepancy statistics. Biometrika 85(4), 967–972.CrossRefGoogle Scholar
Crepon, B., Kramarz, F., & Trognon, A. (1997) Parameters of interest, nuisance parameters and orthogonality conditions: An application to autoregressive error component models. Journal of Econometrics 82(1), 135–156.CrossRefGoogle Scholar
DiCiccio, T., Hall, P., & Romano, J. (1991) Empirical likelihood is Bartlett-correctable. Annals of Statistics 19(2), 1053–1061.CrossRefGoogle Scholar
Dufour, J.-M., Trognon, A., & Tuvaandorj, P. (2017) Invariant tests based on M-estimators, estimating functions, and the generalized method of moments. Econometric Reviews 36(1–3), 182–204.CrossRefGoogle Scholar
Fan, Y., Pastorello, S., & Renault, E. (2015) Maximization by parts in extremum estimation. Econometrics Journal 18(2), 147–17.CrossRefGoogle Scholar
Frazier, D.T. & Renault, E. (2017) Efficient two-step estimation via targeting. Journal of Econometrics 201, 212–227.CrossRefGoogle Scholar
Gänsler, P. & Stute, W. (1977) Wahrscheinlichkeitstheorie. Springer Verlag.CrossRefGoogle Scholar
Gouriéroux, C., Monfort, A., & Renault, E. (1996) Two-stage generalized moment method with applications to regressions with heteroscedasticity of unknown form. Journal of Statistical Planning and Inference 50(1), 37–63.CrossRefGoogle Scholar
Guggenberger, P. (2008) Finite sample evidence suggesting a heavy tail problem of the generalized empirical likelihood estimator. Econometric Reviews 26(4–6), 526–541.CrossRefGoogle Scholar
Guggenberger, P. & Smith, R.J. (2005) Generalized empirical likelihood estimation and tests under partial, weak and strong identification. Econometric Theory 21, 667–709.CrossRefGoogle Scholar
Hall, P. & Heyde, C. (1980) Martingale Limit Theory and its Applications. Academic Press.Google Scholar
Hansen, L.P., Heaton, J., & Yaron, A. (1996) Finite-sample properties of some alternative GMM estimators. Journal of Business & Economic Statistics 14(3), 262–280.Google Scholar
Hausman, J., Lewis, R., Menzel, K., & Newey, W. (2011) Properties of the CUE estimator and a modification with moments. Journal of Econometrics 165(1), 45–57.CrossRefGoogle Scholar
Heckman, J.J. (1976) The common structure of statistical models of truncation, sample selection, and limited dependent variables and a simple estimator for such models. Annals of Economic and Social Measurement 5, 475–492.Google Scholar
Imbens, G.W. (1997) One-step estimators for over-identified generalized method of moments models. Review of Economic Studies 64(3), 359–383.CrossRefGoogle Scholar
Imbens, G.W., Spady, R.H., & Johnson, P. (1998) Information theoretic approaches to inference in moment condition models. Econometrica 66(2), 333–357.CrossRefGoogle Scholar
Jin, F. & Lee, L.-F. (2019) GEL estimation and tests of spatial autoregressive models. Journal of Econometrics 208(2), 585–612.CrossRefGoogle Scholar
Jin, F., Lee, L.-F., & Yu, J. (2018) Sequential and Efficient GMM Estimation of Dynamic Short Panel Data Models. Working Paper, Fudan University.Google Scholar
Kelejian, H.H. & Prucha, I.R. (2001) On the asymptotic distribution of the Moran $I$ test statistic with applications. Journal of Econometrics 104, 219–257.CrossRefGoogle Scholar
Kitamura, Y. (2001) Asymptotic optimality of empirical likelihood for testing moment restrictions. Econometrica 69(6), 1661–1672.CrossRefGoogle Scholar
Kitamura, Y. & Stutzer, M. (1997) An information-theoretical alternative to generalized method of moments estimation. Econometrica 65, 861–874.CrossRefGoogle Scholar
Lazar, N.A. & Mykland, P.A. (1999) Empirical likelihood in the presence of nuisance parameters. Biometrika 86(1), 203–211.CrossRefGoogle Scholar
Lee, L.-F. (2007) GMM and 2SLS estimation of mixed regressive, spatial autoregressive models. Journal of Econometrics 137, 489–514.CrossRefGoogle Scholar
Lee, L.-F. & Yu, J. (2012) The $C\left(\alpha \right)$-type gradient test for spatial dependence in spatial autoregressive models. Letters in Spatial and Resource Sciences 5(3), 119–135.CrossRefGoogle Scholar
Mittelhammer, R.C., Judge, G.G., & Schoenberg, R. (2005) Empirical evidence concerning the finite sample performance of EL-type structural equation estimation and inference methods. In Andrews, D.W.K. & Stock, J.H. (eds.), Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg, pp. 282–305. Cambridge University Press.CrossRefGoogle Scholar
Moran, P.A.P. (1950) Notes on continuous stochastic phenomena. Biometrika 35, 255–260.Google Scholar
Nagar, A.L. (1959) The bias and moment matrix of the general k-class estimators of the parameters in simultaneous equations. Econometrica 27, 575–595.CrossRefGoogle Scholar
Newey, W.K. (1984) A method of moments interpretation of sequential estimators. Economics Letters 14, 201–206.CrossRefGoogle Scholar
Newey, W.K., Ramalho, J.J., & Smith, R.J. (2005) Asymptotic bias for GMM and GEL estimators with estimated nuisance parameters. In Andrews, D.W.K. & Stock, J.H. (eds.), Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg, pp. 245–281. Cambridge University Press.CrossRefGoogle Scholar
Newey, W.K. & Smith, R.J. (2004) Higher order properties of GMM and generalized empirical likelihood estimators. Econometrica 72(1), 219–255.CrossRefGoogle Scholar
Neyman, J. (1959) Optimal asymptotic tests of composite statistical hypotheses. In Grenander, U. (ed.), Probability and Statistics, the Harald Cramer Volume. Wiley.Google Scholar
Otsu, T. (2010) On Bahadur efficiency of empirical likelihood. Journal of Econometrics 157, 248–256.CrossRefGoogle Scholar
Owen, A. (1991) Empirical likelihood for linear models. Annals of Statistics 19, 1725–1747.CrossRefGoogle Scholar
Pagan, A. (1984) Econometric issues in the analysis of regressions with generated regressors. International Economic Review 25(1), 221–247.CrossRefGoogle Scholar
Pagan, A. (1986) Two stage and related estimators and their applications. Review of Economic Studies 53(4), 517–538.CrossRefGoogle Scholar
Qin, J. & Lawless, J. (1994) Empirical likelihood and general estimating equations. Annals of Statistics 22, 300–325.CrossRefGoogle Scholar
Ramalho, J.J. (2002) Alternative estimation methods and specification tests for moment condition models. Ph.D. thesis, University of Bristol.Google Scholar
Rivers, D. & Vuong, Q.H. (1988) Limited information estimators and exogeneity tests for simultaneous probit models. Journal of Econometrics 39(3), 347–366.CrossRefGoogle Scholar
Rothenberg, T.J. (1984) Approximating the distributions of econometric estimators and test statistics. In Griliches, Z. & Intriligator, M.D. (eds.), Handbook of Econometrics, vol. II, pp. 881–935. Elsevier Science Publishers BV.CrossRefGoogle Scholar
Ruud, P.A. (2000) An Introduction to Classical Econometric Theory. Oxford University Press.Google Scholar
Smith, R.J. (1997) Alternative semi-parametric likelihood approaches to generalized method of moments estimation. Economic Journal 107, 503–519.CrossRefGoogle Scholar
Smith, R.J. (2011) GEL criteria for moment condition models. Econometric Theory 27, 1192–1235.CrossRefGoogle Scholar
Song, P.X.-K., Fan, Y., & Kalbfleisch, J.D. (2005) Maximization by parts in likelihood inference. Journal of the American Statistical Association 100(472), 1145–1158.CrossRefGoogle Scholar
Staiger, D. & Stock, J.H. (1997) Instrumental variables regression with weak instruments. Econometrica 65, 557–586.CrossRefGoogle Scholar
Stock, J.H. & Wright, J.H. (2000) GMM with weak identification. Econometrica 68(5), 1055–1096.CrossRefGoogle Scholar
Trognon, A. & Gouriéroux, C. (1990) A note on the efficiency of two-step estimation methods. In Champsaur, P. (ed.), Essays in Honor of Edmond Malinvaud 3, pp. 232–248. MIT Press.Google Scholar
Wilde, J. (2008) A note on GMM estimation of probit models with endogenous regressors. Statistical Paper 49, 471–484.CrossRefGoogle Scholar
Supplementary material: PDF

Jin and Lee supplementary material

Jin and Lee supplementary material

Download Jin and Lee supplementary material(PDF)
PDF 413.6 KB