Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T22:19:57.375Z Has data issue: false hasContentIssue false
  • English
  • Français

DIFFERENCING TRANSFORMATIONS AND INFERENCE IN PREDICTIVE REGRESSION MODELS

Published online by Cambridge University Press:  09 October 2014

Lorenzo Camponovo
Lorenzo Camponovo*
Affiliation:
University of St. Gallen
*
*Address correspondence to Lorenzo Camponovo, School of Economics and Political Science, Department of Economics, University of St. Gallen, Bodanstrasse 6, CH-9000 St. Gallen, Switzerland; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

The limit distribution of conventional test statistics for predictability may depend on the degree of persistence of the predictors. Therefore, diverging results and conclusions may arise because of the different asymptotic theories adopted. Using differencing transformations, we introduce a new class of estimators and test statistics for predictive regression models with Gaussian limit distribution that is instead insensitive to the degree of persistence of the predictors. This desirable feature allows to construct Gaussian confidence intervals for the parameter of interest in stationary, nonstationary, and even locally explosive settings. Besides the limit distribution, we also study the efficiency and the rate of convergence of our new class of estimators. We show that the rate of convergence is 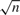$\sqrt n $ in stationary cases, while it can be arbitrarily close to n in nonstationary settings, still preserving the Gaussian limit distribution. Monte Carlo simulations confirm the high reliability and accuracy of our test statistics.

Type
ARTICLES
Information
Econometric Theory , Volume 31 , Issue 6 , December 2015 , pp. 1331 - 1358
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Campbell, J.Y. & Shiller, R.J. (1988) The dividend ratio model and small sample bias: A Monte Carlo study. Economics Letters 29, 325–331.Google Scholar
Campbell, J.Y. & Yogo, M. (2006) Efficient tests of stock return predictability. Journal of Financial Economics 81, 27–60.CrossRefGoogle Scholar
Cavanagh, C., Elliott, G., & Stock, J.H. (1995) Inference in models with nearly integrated regressors. Econometric Theory 11, 1131–1147.Google Scholar
Davidson, J. (1994) Stochastic Limit Theory. Oxford University Press.CrossRefGoogle Scholar
Elliott, G. & Stock, J.H. (1994) Inference in time series regression when the order of integration of a regressor is unknown. Econometric Theory 10, 672–700.CrossRefGoogle Scholar
Fama, E. & French, K. (1988) Dividend yields and expected stock returns. Journal of Financial Economics 22, 3–25.CrossRefGoogle Scholar
Giraitis, L. & Phillips, P.C.B. (2006) Uniform limit theory for stationary autoregression. Journal of Time Series Analysis 27, 51–60.Google Scholar
Han, C., Phillips, P.C.B., & Sul, D. (2011) Uniform asymptotic normality in stationary and unit root autoregression. Econometric Theory 27, 1117–1151.Google Scholar
Han, C., Phillips, P.C.B., & Sul, D. (2014) X-Differencing and dynamic panel model estimation. Econometric Theory 30, 201–251.CrossRefGoogle Scholar
Jansson, M. & Moreira, M.J. (2006) Optimal inference in regression models with nearly integrated regressors. Econometrica 74, 681–714.Google Scholar
Kostakis, A., Magdalinos, T., & Stamatogiannis, M.P. (2012) Robust Econometric Inference for Stock Return Predictability. Working paper.Google Scholar
Loh, W.Y. (1987) Calibrating confidence coefficients. Journal of the American Statistical Association 82, 155–162.Google Scholar
Magdalinos, T. & Phillips, P.C.B. (2009a) Econometric Inference in the Vicinity of Unity. CoFie Working paper, Singapore Management University.Google Scholar
Magdalinos, T. & Phillips, P.C.B. (2009b) Limit theory for cointegrated systems with moderately integrated and moderately explosive regressors. Econometric Theory 25, 482–526.Google Scholar
Mikusheva, A. (2007) Uniform inference in autoregressive models. Econometrica 75, 1411–1452.CrossRefGoogle Scholar
Phillips, P.C.B. (1987) Towards a unified asymptotic theory for autoregression. Biometrika 74, 535–547.CrossRefGoogle Scholar
Phillips, P.C.B. (2014) On confidence intervals for autoregressive roots and predictive regression. Econometrica 82, 1177–1195.Google Scholar
Phillips, P.C.B. & Han, C. (2008) Gaussian inference in AR(1) time series with or without a unit root. Econometric Theory 24, 631–650.Google Scholar
Phillips, P.C.B. & Lee, J.H. (2012) Predictive Regression under Varying Degrees of Persistence and Robust Long-Horizon Regression. Working paper.Google Scholar
Phillips, P.C.B. & Magdalinos, T. (2007) Limit theory for moderate deviations from a unit root. Journal of Econometrics 136, 115–130.CrossRefGoogle Scholar
Phillips, P.C.B. & Solo, V. (1992) Asymptotics for linear processes. Annals of Statistics 20, 971–1001.Google Scholar
Politis, D.N., Romano, J.P., & Wolf, M. (1999) Subsampling. Springer.Google Scholar
Polk, C., Thompson, S., & Vuolteenaho, T. (2006) Cross-sectional forecast of the equity premium. Journal of Financial Economics 81, 101–141.Google Scholar
Stambaugh, R.F. (1999) Predictive regressions. Journal of Financial Economics 54, 375–421.Google Scholar
Torous, W., Valkanov, R., & Yan, S. (2004) On predicting stock returns with nearly integrated explanatory variables. Journal of Business 77, 937–966.Google Scholar