No CrossRef data available.
Article contents
CONSISTENT NON-GAUSSIAN PSEUDO MAXIMUM LIKELIHOOD ESTIMATORS OF SPATIAL AUTOREGRESSIVE MODELS
Published online by Cambridge University Press: 06 February 2023
Abstract
This paper studies the non-Gaussian pseudo maximum likelihood (PML) estimation of a spatial autoregressive (SAR) model with SAR disturbances. If the spatial weights matrix 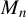 $M_{n}$ for the SAR disturbances is normalized to have row sums equal to 1 or the model reduces to a SAR model with no SAR process of disturbances, the non-Gaussian PML estimator (NGPMLE) for model parameters except the intercept term and the variance
$M_{n}$ for the SAR disturbances is normalized to have row sums equal to 1 or the model reduces to a SAR model with no SAR process of disturbances, the non-Gaussian PML estimator (NGPMLE) for model parameters except the intercept term and the variance 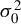 $\sigma _{0}^{2}$ of independent and identically distributed (i.i.d.) innovations in the model is consistent. Without row normalization of
$\sigma _{0}^{2}$ of independent and identically distributed (i.i.d.) innovations in the model is consistent. Without row normalization of 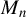 $M_{n}$, the symmetry of i.i.d. innovations leads to consistent NGPMLE for model parameters except
$M_{n}$, the symmetry of i.i.d. innovations leads to consistent NGPMLE for model parameters except 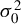 $\sigma _{0}^{2}$. With neither row normalization of
$\sigma _{0}^{2}$. With neither row normalization of 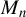 $M_{n}$ nor the symmetry of innovations, a location parameter can be added to the non-Gaussian pseudo likelihood function to achieve consistent estimation of model parameters except
$M_{n}$ nor the symmetry of innovations, a location parameter can be added to the non-Gaussian pseudo likelihood function to achieve consistent estimation of model parameters except 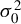 $\sigma _{0}^{2}$. The NGPMLE with no added parameter can have a significant efficiency improvement upon the Gaussian PML estimator and the generalized method of moments estimator based on linear and quadratic moments. We also propose a non-Gaussian score test for spatial dependence, which can be locally more powerful than the Gaussian score test. Monte Carlo results show that our NGPMLE with no added parameter and the score test based on it perform well in finite samples.
$\sigma _{0}^{2}$. The NGPMLE with no added parameter can have a significant efficiency improvement upon the Gaussian PML estimator and the generalized method of moments estimator based on linear and quadratic moments. We also propose a non-Gaussian score test for spatial dependence, which can be locally more powerful than the Gaussian score test. Monte Carlo results show that our NGPMLE with no added parameter and the score test based on it perform well in finite samples.
- Type
- ARTICLES
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
We are very grateful to the Editor (Peter Phillips), the Co-Editor (Dennis Kristensen), and two anonymous referees for helpful comments that led to substantial improvements of this paper. We also thank Zaichao Du, Zhonghao Fu, Gaosheng Ju, Lung-Fei Lee, Hongjun Li, Xi Qu, Ke Miao, Qiao Wang, Xiaohu Wang, Xingbai Xu, and seminar participants at Fudan University and the 2021 Symposium on Econometrics and Big Data at Xiamen University for helpful comments. Fei Jin gratefully acknowledges the financial support from the National Natural Science Foundation of China (NNSFC) (Nos. 71973030 and 71833004). Yuqin Wang thanks the NNSFC financial support under No. 72103122.


