Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T18:36:31.441Z Has data issue: false hasContentIssue false
  • English
  • Français

COINTEGRATION AND REPRESENTATION OF COINTEGRATED AUTOREGRESSIVE PROCESSES IN BANACH SPACES

Published online by Cambridge University Press:  20 April 2022

Won-Ki Seo
Won-Ki Seo*
Affiliation:
University of Sydney
*
Address correspondence to Won-Ki Seo, School of Economics, University of Sydney, Sydney, NSW, Australia; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the notion of cointegration for time series taking values in a potentially infinite dimensional Banach space. Examples of such time series include stochastic processes in 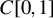$C[0,1]$ equipped with the supremum distance and those in a finite dimensional vector space equipped with a non-Euclidean distance. We then develop versions of the Granger–Johansen representation theorems for I(1) and I(2) autoregressive (AR) processes taking values in such a space. To achieve this goal, we first note that an AR(p) law of motion can be characterized by a linear operator pencil (an operator-valued map with certain properties) via the companion form representation, and then study the spectral properties of a linear operator pencil to obtain a necessary and sufficient condition for a given AR(p) law of motion to admit I(1) or I(2) solutions. These operator-theoretic results form a fundamental basis for our representation theorems. Furthermore, it is shown that our operator-theoretic approach is in fact a closely related extension of the conventional approach taken in a Euclidean space setting. Our theoretical results may be especially relevant in a recently growing literature on functional time series analysis in Banach spaces.

Type
ARTICLES
Information
Econometric Theory , Volume 39 , Issue 4 , August 2023 , pp. 737 - 788
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Footnotes

This article benefited from the helpful suggestions for improvement made by the Editor, Peter C.B. Phillips, and three anonymous reviewers, to whom I express my thanks.

References

REFERENCES

Abramovich, Y.A. & Aliprantis, C.D. (2002) An Invitation to Operator Theory , Vol. 1. American Mathematical Society.Google Scholar
Albrecht, A., Avrachenkov, K., Beare, B., Boland, J., Franchi, M., & Howlett, P. (2021) The resolution and representation of time series in Banach space. Preprint, arXiv:2105.14393 [math.FA].Google Scholar
Albrecht, A., Howlett, P., & Verma, G. (2019) The fundamental equations for the generalized resolvent of an elementary pencil in a unital Banach algebra. Linear Algebra and Its Applications 574, 216–251.CrossRefGoogle Scholar
Albrecht, A.R., Howlett, P.G., & Pearce, C.E.M. (2011) Necessary and sufficient conditions for the inversion of linearly-perturbed bounded linear operators on Banach space using Laurent series. Journal of Mathematical Analysis and Applications 383(1), 95–110.CrossRefGoogle Scholar
Amouch, M., Abdellah, G., & Messirdi, B. (2015) A spectral analysis of linear operator pencils on Banach spaces with application to quotient of bounded operators. International Journal of Analysis and Applications 7(2), 104–128.Google Scholar
Bart, H., Gohberg, I., Kaashoek, M., & Ran, A.C.M. (2007) Factorization of Matrix and Operator Functions: The State Space Method . Birkhäuser.Google Scholar
Beare, B.K., Seo, J., & Seo, W.-K. (2017) Cointegrated linear processes in Hilbert space. Journal of Time Series Analysis 38(6), 1010–1027.CrossRefGoogle Scholar
Beare, B.K. & Seo, W.-K. (2020) Representation of I(1) and I(2) autoregressive Hilbertian processes. Econometric Theory 36(5), 773–802.CrossRefGoogle Scholar
Bosq, D. (2000) Linear Processes in Function Spaces . Springer.CrossRefGoogle Scholar
Bosq, D. (2002) Estimation of mean and covariance operator of autoregressive processes in Banach spaces. Statistical Inference for Stochastic Processes 5(3), 287–306.CrossRefGoogle Scholar
Chang, Y., Hu, B., & Park, J.Y. (2016a) On the Error Correction Model for Functional Time Series with Unit Roots. Mimeo, Indiana University.Google Scholar
Chang, Y., Kim, C.S., & Park, J.Y. (2016b) Nonstationarity in time series of state densities. Journal of Econometrics 192(1), 152–167.CrossRefGoogle Scholar
Conway, J.B. (1994) A Course in Functional Analysis . Springer.Google Scholar
Dehling, H. & Sharipov, O.S. (2005) Estimation of mean and covariance operator for Banach space valued autoregressive processes with dependent innovations. Statistical Inference for Stochastic Processes 8(2), 137–149.CrossRefGoogle Scholar
Dette, H., Kokot, K., & Aue, A. (2020) Functional data analysis in the Banach space of continuous functions. Annals of Statistics 48(2), 1168–1192.CrossRefGoogle Scholar
Engl, H.W. & Nashed, M. (1981) Generalized inverses of random linear operators in Banach spaces. Journal of Mathematical Analysis and Applications 83(2), 582–610.CrossRefGoogle Scholar
Engle, R.F. & Granger, C.W.J. (1987) Co-integration and error correction: Representation, estimation, and testing. Econometrica 55(2), 251–276.CrossRefGoogle Scholar
Engsted, T. & Johansen, S. (1999) Granger’s representation theorem and multicointegration. In Engle, R.F. & White, H. (eds), Cointegration, Causality and Forecasting: A Festschrift in Honour of Clive Granger , pp. 200–212. Oxford University Press.Google Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V., & Zizler, V. (2010) Banach Space Theory . Springer.Google Scholar
Faliva, M. & Zoia, M.G. (2002) On a partitioned inversion formula having useful applications in econometrics. Econometric Theory 18(2), 525–530.CrossRefGoogle Scholar
Faliva, M. & Zoia, M.G. (2010) Dynamic Model Analysis . Springer.Google Scholar
Faliva, M. & Zoia, M.G. (2011) An inversion formula for a matrix polynomial about a (unit) root. Linear and Multilinear Algebra 59, 541–556.CrossRefGoogle Scholar
Faliva, M. & Zoia, M.G. (2021). Cointegrated solutions of unit-root VARs: An extended representation theorem. Preprint, arXiv:2102.10626 [econ.EM].Google Scholar
Franchi, M. & Paruolo, P. (2016) Inverting a matrix function around a singularity via local rank factorization. SIAM Journal on Matrix Analysis and Applications 37(2), 774–797.CrossRefGoogle Scholar
Franchi, M. & Paruolo, P. (2019) A general inversion theorem for cointegration. Econometric Reviews 38(10), 1176–1201.CrossRefGoogle Scholar
Franchi, M. & Paruolo, P. (2020) Cointegration in functional autoregressive processes. Econometric Theory 36(5), 803–839.CrossRefGoogle Scholar
Gao, Y. & Shang, H.L. (2017) Multivariate functional time series forecasting: Application to age-specific mortality rates. Risks 5(2), 21.CrossRefGoogle Scholar
Gohberg, I., Goldberg, S., & Kaashoek, M. (2013) Classes of Linear Operators , Vol. I. Birkhäuser.Google Scholar
Granger, C.W. & Lee, T.-H. (1989) Investigation of production, sales and inventory relationships using multicointegration and non-symmetric error correction models. Journal of Applied Econometrics 4(S1), S145–S159.CrossRefGoogle Scholar
Granger, C.W.J. (1981) Some properties of time series data and their use in econometric model specification. Journal of Econometrics 16(1), 121–130.CrossRefGoogle Scholar
Hansen, P.R. (2005) Granger’s representation theorem: A closed-form expression for I(1) processes. The Econometrics Journal 8(1), 23–38.CrossRefGoogle Scholar
Hörmann, S., Horváth, L., & Reeder, R. (2013) A functional version of the ARCH model. Econometric Theory 29(2), 267–288.CrossRefGoogle Scholar
Horváth, L., Kokoszka, P., & Rice, G. (2014) Testing stationarity of functional time series. Journal of Econometrics 179(1), 66–82.CrossRefGoogle Scholar
Hu, B. & Park, J.Y. (2016) Econometric Analysis of Functional Dynamics in the Presence of Persistence. Mimeo, Indiana University.Google Scholar
Hyndman, R.J. & Ullah, M.S. (2007) Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis 51(10), 4942–4956.CrossRefGoogle Scholar
Johansen, S. (1991) Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 59(6), 1551–1580.CrossRefGoogle Scholar
Johansen, S. (1992) A representation of vector autoregressive processes integrated of order 2. Econometric Theory 8(2), 188–202.CrossRefGoogle Scholar
Johansen, S. (1995) Likelihood-Based Inference in Cointegrated Vector Autoregressive Models . Oxford University Press.CrossRefGoogle Scholar
Johansen, S. (2008) Representation of cointegrated autoregressive processes with application to fractional processes. Econometric Reviews 28(1–3), 121–145.CrossRefGoogle Scholar
Kato, T. (1995) Perturbation Theory for Linear Operators . Springer.CrossRefGoogle Scholar
Kheifets, I.L. & Phillips, P.C.B. (2021). Fully modified least squares cointegrating parameter estimation in multicointegrated systems. Journal of Econometrics , in press.Google Scholar
Kheifets, I.L. & Phillips, P.C.B. (2022). Robust High-Dimensional IV Cointegration Estimation and Inference. Working paper, Yale University.Google Scholar
Labbas, A. & Mourid, T. (2002) Estimation et prévision d’un processus autorégressif Banach. Comptes Rendus Mathematique 335(9), 767–772.CrossRefGoogle Scholar
Laursen, K.B. & Mbekhta, M. (1995) Operators with finite chain length and the ergodic theorem. Proceedings of the American Mathematical Society 123(11), 3443–3448.CrossRefGoogle Scholar
Markus, A.S. (2012) Introduction to the Spectral Theory of Polynomial Operator Pencils (Translations of Mathematical Monographs) . American Mathematical Society.CrossRefGoogle Scholar
Megginson, R.E. (2012) Introduction to Banach Space Theory . Springer.Google Scholar
Nielsen, M.Ø., Seo, W.-K., & Seong, D.. (2019) Inference on the Dimension of the Nonstationary Subspace in Functional Time Series. QED Working paper 1420, Queen’s University.Google Scholar
Petris, G. (2013) A Bayesian framework for functional time series analysis. Preprint, arXiv:1311.0098 [stat.ME].Google Scholar
Phillips, P.C.B. & Solo, V. (1992) Asymptotics for linear processes. Annals of Statistics 20(2), 971–1001.CrossRefGoogle Scholar
Pumo, B. (1998) Prediction of continuous time processes by C[0, 1]-valued autoregressive process. Statistical Inference for Stochastic Processes 1(3), 297–309.CrossRefGoogle Scholar
Ruiz-Medina, M.D. & Álvarez-Liébana, J. (2019) Strongly consistent autoregressive predictors in abstract Banach spaces. Journal of Multivariate Analysis 170, 186–201.CrossRefGoogle Scholar
Schumacher, J.M. (1991) System-theoretic trends in econometrics. In Antoulas, A.C., Mathematical System Theory: The Influence of R.E. Kalman , pp. 559–577. Springer.CrossRefGoogle Scholar
Seo, W.-K. (2020) Functional principal component analysis of cointegrated functional time series. Preprint, arXiv:2011.12781v4 [stat.ME].Google Scholar
Shang, H.L. & Hyndman, R.J. (2017) Grouped functional time series forecasting: An application to age-specific mortality rates. Journal of Computational and Graphical Statistics 26(2), 330–343.CrossRefGoogle Scholar
Shang, H.L., Smith, P.W., Bijak, J., & Wiśniowski, A. (2016) A multilevel functional data method for forecasting population, with an application to the United Kingdom. International Journal of Forecasting 32(3), 629–649.CrossRefGoogle Scholar
Yoo, B.S. (1987) Co-Integrated Time Series: Structure, Forecasting and Testing. Ph.D. dissertation, University of California, San Diego.Google Scholar