Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Preminger, Arie
and
Hafner, Christian M.
2006.
Deciding between GARCH and Stochastic Volatility via Strong Decision Rules.
SSRN Electronic Journal,
Hafner, Christian M.
and
Preminger, Arie
2006.
Asymptotic Theory for a Factor GARCH Model.
SSRN Electronic Journal,
Carnero, M. Angeles
Peña, Daniel
and
Ruiz, Esther
2007.
Effects of outliers on the identification and estimation of GARCH models.
Journal of Time Series Analysis,
Vol. 28,
Issue. 4,
p.
471.
Dahl, Christian
and
Iglesias, Emma M.
2008.
The Limiting Properties of the QMLE in a General Class of Asymmetric Volatility Models.
SSRN Electronic Journal,
Ma, Jun
2008.
A Closed-Form Asymptotic Variance-Covariance Matrix for the Quasi-Maximum Likelihood Estimator of the Garch(1,1) Model.
SSRN Electronic Journal,
Amendola, Alessandra
and
Storti, Giuseppe
2008.
A GMM procedure for combining volatility forecasts.
Computational Statistics & Data Analysis,
Vol. 52,
Issue. 6,
p.
3047.
Renfro, Charles
2009.
The Practice of Econometric Theory.
Vol. 44,
Issue. ,
p.
55.
Hafner, Christian M.
2009.
Complex Systems in Finance and Econometrics.
p.
464.
Hafner, Christian M.
and
Preminger, Arie
2009.
ASYMPTOTIC THEORY FOR A FACTOR GARCH MODEL.
Econometric Theory,
Vol. 25,
Issue. 2,
p.
336.
Hafner, Christian M.
and
Preminger, Arie
2010.
Deciding between GARCH and stochastic volatility via strong decision rules.
Journal of Statistical Planning and Inference,
Vol. 140,
Issue. 3,
p.
791.
Prono, Todd
2011.
Simple, Skewness-Based GMM Estimation of the Semi-Strong GARCH(1,1) Model.
SSRN Electronic Journal,
Andrews, Donald W. K.
and
Guggenberger, Patrik
2011.
A Conditional-Heteroskedasticity-Robust Confidence Interval for the Autoregressive Parameter.
SSRN Electronic Journal,
Chen, Bei
Gel, Yulia R.
Balakrishna, N.
and
Abraham, Bovas
2011.
Computationally efficient bootstrap prediction intervals for returns and volatilities in ARCH and GARCH processes.
Journal of Forecasting,
Vol. 30,
Issue. 1,
p.
51.
Prono, Todd
2011.
When a Factor is Measured with Error: The Role of Conditional Heteroskedasticity in Identifying and Estimating Linear Factor Models.
SSRN Electronic Journal,
Andrews, Donald W. K.
and
Guggenberger, Patrik
2012.
A Conditional-Heteroskedasticity-Robust Confidence Interval for the Autoregressive Parameter.
SSRN Electronic Journal,
Hafner, Christian M.
and
Linton, Oliver B.
2012.
An Almost Closed Form Estimator for the EGARCH Model.
SSRN Electronic Journal,
Bondon, Pascal
and
Bahamonde, Natalia
2012.
Least squares estimation of ARCH models with missing observations.
Journal of Time Series Analysis,
Vol. 33,
Issue. 6,
p.
880.
Sbrana, Giacomo
and
Poloni, Federico
2013.
A closed-form estimator for the multivariate GARCH(1,1)model.
Journal of Multivariate Analysis,
Vol. 120,
Issue. ,
p.
152.
Bibi, Abdelouahab
and
Lescheb, Ines
2013.
Estimation and Asymptotic Properties in PeriodicGARCH(1, 1) Models.
Communications in Statistics - Theory and Methods,
Vol. 42,
Issue. 19,
p.
3497.
Poloni, Federico
and
Sbrana, Giacomo
2014.
Feasible generalized least squares estimation of multivariate GARCH(1, 1) models.
Journal of Multivariate Analysis,
Vol. 129,
Issue. ,
p.
151.
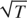 -asymptotic normality when the eighth moment exists. We
demonstrate that a finite number of Newton–Raphson iterations using
our estimator as starting point will yield asymptotically the same
distribution as the QMLE when the fourth moment exists. A simulation study
confirms our theoretical results.The first
author's research was supported by the Shoemaker Foundation. The
second author's research was supported by the Economic and Social
Science Research Council of the United Kingdom.
-asymptotic normality when the eighth moment exists. We
demonstrate that a finite number of Newton–Raphson iterations using
our estimator as starting point will yield asymptotically the same
distribution as the QMLE when the fourth moment exists. A simulation study
confirms our theoretical results.The first
author's research was supported by the Shoemaker Foundation. The
second author's research was supported by the Economic and Social
Science Research Council of the United Kingdom.