Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T18:07:48.708Z Has data issue: false hasContentIssue false
  • English
  • Français

BIAS-REDUCED LOG-PERIODOGRAM AND WHITTLE ESTIMATION OF THE LONG-MEMORY PARAMETER WITHOUT VARIANCE INFLATION

Published online by Cambridge University Press:  30 August 2006

Patrik Guggenberger  and
Yixiao Sun
Patrik Guggenberger
Affiliation:
University of California, Los Angeles
Yixiao Sun
Affiliation:
University of California, San Diego
Get access Rights & Permissions [Opens in a new window]

Abstract

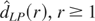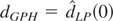The bias-reduced log-periodogram estimator of Andrews and Guggenberger (2003, Econometrica 71, 675–712) for the long-memory parameter d in a stationary long-memory time series reduces the asymptotic bias of the original log-periodogram estimator of Geweke and Porter-Hudak (1983) by an order of magnitude but inflates the asymptotic variance by a multiplicative constant cr, for example, c1 = 2.25 and c2 = 3.52. In this paper, we introduce a new, computationally attractive estimator 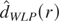by taking a weighted average of 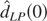estimators over different bandwidths. We show that, for each fixed r ≥ 0, the new estimator can be designed to have the same asymptotic bias properties as 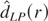but its asymptotic variance is changed by a constant cr* that can be chosen to be as small as desired, in particular smaller than cr. 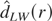The same idea is also applied to the local-polynomial Whittle estimator in Andrews and Sun (2004, Econometrica 72, 569–614) leading to the weighted estimator 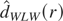. We establish the asymptotic bias, variance, and mean-squared error of the weighted estimators and show their asymptotic normality. Furthermore, we introduce a data-dependent adaptive procedure for selecting r and the bandwidth m and show that up to a logarithmic factor, the resulting adaptive weighted estimator achieves the optimal rate of convergence. A Monte Carlo study shows that the adaptive weighted estimator compares very favorably to several other adaptive estimators.We thank a co-editor and three referees for very helpful suggestions. We are grateful for the constructive comments offered by Marc Henry, Javier Hidalgo, and especially Katsumi Shimotsu.

Type
Research Article
Information
Econometric Theory , Volume 22 , Issue 5 , October 2006 , pp. 863 - 912
Copyright
© 2006 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agiakloglou, C., P. Newbold, & M. Wohar (1993) Bias in an estimator of the fractional difference parameter. Journal of Time Series Analysis 14, 235–246.Google Scholar
Andrews, D.W.K. & P. Guggenberger (2003) A bias-reduced log-periodogram regression estimator for the long-memory parameter. Econometrica 71, 675–712.Google Scholar
Andrews, D.W.K. & Y. Sun (2004) Adaptive local polynomial Whittle estimation of long-range dependence. Econometrica 72, 569–614.Google Scholar
Brillinger, D.R. (1975) Time Series, Data Analysis and Theory. Holden-Day.
Davidson, R. & J.G. MacKinnon (1993) Estimation and Inference in Econometrics. Oxford University Press.
Geweke, J. & S. Porter-Hudak (1983) The estimation and application of long-memory time series models. Journal of Time Series Analysis 4, 221–237.Google Scholar
Giraitis, L., P.M. Robinson, & A. Samarov (2000) Adaptive semiparametric estimation of the memory parameter. Journal of Multivariate Analysis 72, 183–207.Google Scholar
Gray, H.L. & W.R. Schucany (1972) The Generalized Jackknife Statistic. Dekker.
Guggenberger, P. & Y. Sun (2003) Bias-Reduced Log-Periodogram and Whittle Estimation of the Long-Memory Parameter without Variance Inflation. (Previous version of this paper, available from the authors upon request.)
Härdle, W. (1990) Applied Nonparametric Regression. Cambridge University Press.
Hidalgo, J. (2005) Semiparametric estimation for stationary processes whose spectra have an unknown pole. Annals of Statistics 33, 1843–1889.Google Scholar
Hurvich, C.M. (2001) Model selection for broadband semiparametric estimation of long memory in time series. Journal of Time Series Analysis 22, 679–709.Google Scholar
Hurvich, C.M. & J. Brodsky (2001) Broadband semiparametric estimation of the memory parameter of a long-memory time series using fractional exponential models. Journal of Time Series Analysis 22, 221–249.Google Scholar
Hurvich, C.M. & R.S. Deo (1999) Plug-in selection of the number of frequencies in regression estimates of the memory parameter of a long-memory time series. Journal of Time Series Analysis 20, 331–341.Google Scholar
Hurvich, C.M., R.S. Deo, & J. Brodsky (1998) The mean squared error of Geweke and Porter-Hudak's estimator of the memory parameter of a long-memory time series. Journal of Time Series Analysis 19, 19–46.Google Scholar
Hurvich, C.M., E. Moulines, & P. Soulier (2002) The FEXP estimator for potentially non-stationary linear time series. Stochastic Processes and Their Applications 97, 307–340.Google Scholar
Iouditsky, A., E. Moulines, & P. Soulier (2001) Adaptive estimation of the fractional differencing coefficient. Bernoulli 7, 699–731.Google Scholar
Kim, C.S. & P.C.B. Phillips (1999a) Log Periodogram Regression: The Nonstationary Case. Working paper, Cowles Foundation, Yale University.
Kim, C.S. & P.C.B. Phillips (1999b) Modified Log Periodogram Regression. Working paper, Cowles Foundation, Yale University.
Künsch, H.R. (1987) Statistical aspects of self-similar processes. In Y. Prohorov & V.V. Sazanov (eds.), Proceedings of the First World Congress of the Bernoulli Society, vol. 1, pp. 67–74. VNU Science Press.
Lepskii, O.V. (1990) On a problem of adaptive estimation in Gaussian white noise. Theory of Probability and Its Applications 35, 454–466.Google Scholar
Lobato, I.N. (1999) A semiparametric two step estimator in a multivariate long memory model. Journal of Econometrics 90, 129–153.Google Scholar
Moulines, E. & P. Soulier (1999) Broadband log-periodogram regression of time series with long-range dependence. Annals of Statistics 27, 1415–1439.Google Scholar
Moulines, E. & P. Soulier (2000) Data driven order selection for projection estimator of the spectral density of time series with long range dependence. Journal of Time Series Analysis 21, 193–218.Google Scholar
Phillips, P.C.B. & K. Shimotsu (2004) Local Whittle estimation in nonstationary and unit root cases. Annals of Statistics 32, 656–692.Google Scholar
Robinson, P.M. (1995a) Gaussian semiparametric estimation of long range dependence. Annals of Statistics 23, 1630–1661.Google Scholar
Robinson, P.M. (1995b) Log-periodogram regression of time series with long range dependence. Annals of Statistics 23, 1048–1072.Google Scholar
Robinson, P.M. & M. Henry (2003) Higher-order kernel semiparametric M-estimation of long memory. Journal of Econometrics 114, 1–27.Google Scholar
Shimotsu, K. & P.C.B. Phillips (2005) Exact local Whittle estimation of fractional integration. Annals of Statistics 33, 1890–1933.Google Scholar
Velasco, C. (1999) Non-stationary log-periodogram regression. Journal of Econometrics 91, 325–371.Google Scholar
Velasco, C. (2000) Non-Gaussian log-periodogram regression. Econometric Theory 16, 44–79.Google Scholar
Velasco, C. & P.M. Robinson (2000) Whittle pseudo-maximum likelihood estimation for nonstationary time series. Journal of the American Statistical Association 95, 1229–1243.Google Scholar
Walter, W. (1992) Analysis I. Springer-Verlag.