Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Andreou, Elena
and
Werker, Bas J. M.
2003.
A Simple Asymptotic Analysis of Residual-Based Statistics.
SSRN Electronic Journal,
Andreou, Elena
and
Werker, Bas J. M.
2004.
An Alternative Asymptotic Analysis of Residual-Based Statistics.
SSRN Electronic Journal,
Hidalgo, Javier
and
Zaffaroni, Paolo
2007.
A goodness-of-fit test for models.
Journal of Econometrics,
Vol. 141,
Issue. 2,
p.
973.
Giraitis, Liudas
Leipus, Remigijus
and
Surgailis, Donatas
2007.
Long Memory in Economics.
p.
3.
Hidalgo, Javier
and
Zaffaroni, Paolo
2007.
A goodness-of-fit test for ARCH(∞) models.
Journal of Econometrics,
Vol. 141,
Issue. 2,
p.
835.
Chen, Yi‐Ting
2008.
A unified approach to standardized‐residuals‐based correlation tests for GARCH‐type models.
Journal of Applied Econometrics,
Vol. 23,
Issue. 1,
p.
111.
Zhu, Fukang
and
Wang, Dehui
2010.
Diagnostic checking integer-valued ARCH models using conditional residual autocorrelations.
Computational Statistics & Data Analysis,
Vol. 54,
Issue. 2,
p.
496.
2010.
GARCH Models.
p.
473.
Gong, Yun
Li, Zhouping
and
Peng, Liang
2010.
Empirical likelihood intervals for conditional Value-at-Risk in ARCH/GARCH models.
Journal of Time Series Analysis,
Vol. 31,
Issue. 2,
p.
65.
Francq, Christian
and
Zakoïan, Jean-Michel
2010.
Inconsistency of the MLE and inference based on weighted LS for LARCH models.
Journal of Econometrics,
Vol. 159,
Issue. 1,
p.
151.
Kirch, Claudia
and
Kamgaing, Joseph Tadjuidje
2012.
Testing for parameter stability in nonlinear autoregressive models.
Journal of Time Series Analysis,
Vol. 33,
Issue. 3,
p.
365.
Zhu, Ke.
2013.
A mixed portmanteau test for ARMA‐GARCH models by the quasi‐maximum exponential likelihood estimation approach.
Journal of Time Series Analysis,
Vol. 34,
Issue. 2,
p.
230.
Andreou, Elena
and
Werker, Bas J. M.
2013.
Residual-Based Rank Specification Tests for AR-GARCH Type Models.
SSRN Electronic Journal,
Ghoudi, Kilani
and
Rémillard, Bruno
2014.
Comparison of specification tests for GARCH models.
Computational Statistics & Data Analysis,
Vol. 76,
Issue. ,
p.
291.
Ghoudi, Kilani
and
Remillard, Bruno
2014.
Tests of Randomness for Time Series.
SSRN Electronic Journal,
Andreou, Elena
and
Werker, Bas J.M.
2015.
Residual-based rank specification tests for AR–GARCH type models.
Journal of Econometrics,
Vol. 185,
Issue. 2,
p.
305.
Hong, Yongmiao
and
Lee, Yoon-Jin
2017.
A General Approach to Testing Volatility Models in Time Series.
Journal of Management Science and Engineering,
Vol. 2,
Issue. 1,
p.
1.
2018.
Linear Models and Time‐Series Analysis.
p.
825.
2019.
GARCH Models.
p.
467.
Rasekhi, Saeed
and
Nabavi, Nasim
2020.
Do Derivatives Hinder the Financial Contagion? A Case Study of Developed Countries’ Stock Markets.
Journal of Business Strategy Finance and Management,
Vol. 2,
Issue. 1-2,
p.
89.
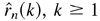 ,
k ≥ 1, these autocorrelations computed from a realization
of length n, we show that the statistic
,
k ≥ 1, these autocorrelations computed from a realization
of length n, we show that the statistic
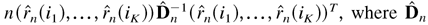 is a matrix computed from the data, converges to the chi-square distribution
with K degrees of freedom for any 1 ≤ i1 <
··· < iK. Our
results are valid under weak assumptions on the innovations and model
coefficients that admit that arbitrary low-order moments of the
observations can be infinite. The matrix
is a matrix computed from the data, converges to the chi-square distribution
with K degrees of freedom for any 1 ≤ i1 <
··· < iK. Our
results are valid under weak assumptions on the innovations and model
coefficients that admit that arbitrary low-order moments of the
observations can be infinite. The matrix
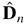 and its asymptotic limit D depend on the distribution of the
innovations. A small simulation study illustrates the theory and shows, in
particular, that using the matrix D computed under the assumption of
normal innovations may lead to incorrect conclusions if the innovations have
a different distribution.We thank the two
referees for their comments and Professor Bruce E. Hansen, the co-editor
in charge, for his sound advice on how to improve the paper. The work of
István Berkes was supported by the Hungarian National Foundation for
Scientific Research, grant T 29621. The work of Lajos Horváth and
Piotr Kokoszka was supported by NATO grant PST.CLG.977607.
and its asymptotic limit D depend on the distribution of the
innovations. A small simulation study illustrates the theory and shows, in
particular, that using the matrix D computed under the assumption of
normal innovations may lead to incorrect conclusions if the innovations have
a different distribution.We thank the two
referees for their comments and Professor Bruce E. Hansen, the co-editor
in charge, for his sound advice on how to improve the paper. The work of
István Berkes was supported by the Hungarian National Foundation for
Scientific Research, grant T 29621. The work of Lajos Horváth and
Piotr Kokoszka was supported by NATO grant PST.CLG.977607.