Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T18:26:02.914Z Has data issue: false hasContentIssue false
  • English
  • Français

ANALYSIS OF GLOBAL AND LOCAL OPTIMA OF REGULARIZED QUANTILE REGRESSION IN HIGH DIMENSIONS: A SUBGRADIENT APPROACH

Published online by Cambridge University Press:  18 October 2022

Lan Wang Open the ORCID record for Lan Wang [Opens in a new window]  and
Xuming He Open the ORCID record for Xuming He [Opens in a new window]
Lan Wang*
Affiliation:
University of Miami
Xuming He
Affiliation:
University of Michigan
*
Address correspondence to Lan Wang, Department of Management Science, University of Miami, Coral Gables, FL 33146, USA; e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Regularized quantile regression (QR) is a useful technique for analyzing heterogeneous data under potentially heavy-tailed error contamination in high dimensions. This paper provides a new analysis of the estimation/prediction error bounds of the global solution of 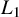$L_1$-regularized QR (QR-LASSO) and the local solutions of nonconvex regularized QR (QR-NCP) when the number of covariates is greater than the sample size. Our results build upon and significantly generalize the earlier work in the literature. For certain heavy-tailed error distributions and a general class of design matrices, the least-squares-based LASSO cannot achieve the near-oracle rate derived under the normality assumption no matter the choice of the tuning parameter. In contrast, we establish that QR-LASSO achieves the near-oracle estimation error rate for a broad class of models under conditions weaker than those in the literature. For QR-NCP, we establish the novel results that all local optima within a feasible region have desirable estimation accuracy. Our analysis applies to not just the hard sparsity setting commonly used in the literature, but also to the soft sparsity setting which permits many small coefficients. Our approach relies on a unified characterization of the global/local solutions of regularized QR via subgradients using a generalized Karush–Kuhn–Tucker condition. The theory of the paper establishes a key property of the subdifferential of the quantile loss function in high dimensions, which is of independent interest for analyzing other high-dimensional nonsmooth problems.

Type
ARTICLES
Information
Econometric Theory , Volume 40 , Issue 2 , April 2024 , pp. 233 - 277
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Footnotes

Wang and He’s research is partly supported by NSF FRGMS-1952373. The authors are grateful to the Co-Editor and two anonymous referees, whose comments have helped to significantly improve the paper. They also thank Dr. Alexander Giessing for his helpful comments and Dr. Yunan Wu for her latex help on an earlier draft of the paper. Part of the results developed in this paper were made available as an earlier technical report (Wang, 2019).

References

REFERENCES

Abadie, A., Angrist, J., & Imbens, G. (2002) Instrumental variables estimates of the effect of subsidized training on the quantiles of trainee earnings. Econometrica 70(1), 91–117.CrossRefGoogle Scholar
Angrist, J., Chernozhukov, V., & Fernández-Val, I. (2006) Quantile regression under misspecification, with an application to the US wage structure. Econometrica 74(2), 539–563.CrossRefGoogle Scholar
Arellano, M. & Bonhomme, S. (2017) Quantile selection models with an application to understanding changes in wage inequality. Econometrica 85(1), 1–28.CrossRefGoogle Scholar
Belloni, A. & Chernozhukov, V. (2011) L1-penalized quantile regression in high-dimensional sparse models. Annals of Statistics 39, 82–130.CrossRefGoogle Scholar
Belloni, A., Chernozhukov, V., & Kato, K. (2014) Uniform post-selection inference for least absolute deviation regression and other z-estimation problems. Biometrika 102(1), 77–94.CrossRefGoogle Scholar
Belloni, A., Chernozhukov, V., & Kato, K. (2019) Valid post-selection inference in high-dimensional approximately sparse quantile regression models. Journal of the American Statistical Association 114(526), 749–758.CrossRefGoogle Scholar
Bickel, P.J., Ritov, Y., & Tsybakov, A.B. (2009) Simultaneous analysis of Lasso and Dantzig selector. Annals of Statistics 37(4), 1705–1732.CrossRefGoogle Scholar
Bradic, J., Fan, J., & Wang, W. (2011) Penalized composite quasi-likelihood for ultrahigh dimensional variable selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73(3), 325–349.CrossRefGoogle ScholarPubMed
Bradic, J. & Kolar, M. (2017). Uniform inference for high-dimensional quantile regression: Linear functionals and regression rank scores. Preprint, arXiv:1702.06209.Google Scholar
Buchinsky, M. (1994) Changes in the US wage structure 1963–1987: Application of quantile regression. Econometrica 62, 405–458.CrossRefGoogle Scholar
Buchinsky, M. (1998) The dynamics of changes in the female wage distribution in the USA: A quantile regression approach. Journal of Applied Econometrics 13(1), 1–30.3.0.CO;2-A>CrossRefGoogle Scholar
Bunea, F., Tsybakov, A., & Wegkamp, M. (2007) Sparsity oracle inequalities for the Lasso. Electronic Journal of Statistics 1, 169–194.CrossRefGoogle Scholar
Chamberlain, G. (1994) Quantile regression, censoring, and the structure of wages. In C.A. Sims (ed.), Advances in Econometrics: Sixth World Congress, vol. 2. Cambridge University Press, pp. 171–209.CrossRefGoogle Scholar
Chen, X., Li, D., Li, Q., & Li, Z. (2019a) Nonparametric estimation of conditional quantile functions in the presence of irrelevant covariates. Journal of Econometrics 212(2), 433–450.CrossRefGoogle Scholar
Chen, X., Liu, W., & Zhang, Y. (2019b) Quantile regression under memory constraint. Annals of Statistics 47(6), 3244–3273.Google Scholar
Chernozhukov, V. & Fernández-Val, I. (2011) Inference for extremal conditional quantile models, with an application to market and birthweight risks. The Review of Economic Studies 78(2), 559–589.CrossRefGoogle Scholar
Chernozhukov, V., Fernández-Val, I., Hahn, J., & Newey, W. (2013) Average and quantile effects in nonseparable panel models. Econometrica 81(2), 535–580.Google Scholar
Donoho, D.L. & Johnstone, I.M. (1994). Minimax risk over ${l}_p$ -balls for ${l}_q$ -error. Probability Theory and Related Fields 99(2), 277–303.CrossRefGoogle Scholar
Elsener, A. & van de Geer, S. (2018) Sharp oracle inequalities for stationary points of nonconvex penalized m-estimators. IEEE Transactions on Information Theory 65(3), 1452–1472.CrossRefGoogle Scholar
Fan, J., Fan, Y., & Barut, E. (2014) Adaptive robust variable selection. Annals of Statistics 42(1), 324–351.CrossRefGoogle ScholarPubMed
Fan, J., Li, Q., & Wang, Y. (2017) Estimation of high dimensional mean regression in the absence of symmetry and light tail assumptions. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 79(1), 247–265.CrossRefGoogle ScholarPubMed
Fan, J. & Li, R. (2001) Variable selection via nonconcave penalized likelihood and its oracle property. Journal of the American Statistical Association 96, 1348–1360.CrossRefGoogle Scholar
Fan, Z. & Lian, H. (2018) Quantile regression for additive coefficient models in high dimensions. Journal of Multivariate Analysis 164, 54–64.CrossRefGoogle Scholar
Firpo, S., Fortin, N.M., & Lemieux, T. (2009) Unconditional quantile regressions. Econometrica 77(3), 953–973.Google Scholar
Fitzenberger, B., Koenker, R., & Machado, J.A. (2013) Economic Applications of Quantile Regression. Springer Science & Business Media.Google Scholar
Galvao, A.F., Lamarche, C., & Lima, L.R. (2013) Estimation of censored quantile regression for panel data with fixed effects. Journal of the American Statistical Association 108(503), 1075–1089.CrossRefGoogle Scholar
Graham, B.S., Hahn, J., Poirier, A., & Powell, J.L. (2018) A quantile correlated random coefficients panel data model. Journal of Econometrics 206(2), 305–335.CrossRefGoogle Scholar
Greenshtein, E., Ritov, Y. (2004) Persistence in high-dimensional linear predictor selection and the virtue of overparametrization. Bernoulli 10(6), 971–988.CrossRefGoogle Scholar
Harding, M. & Lamarche, C. (2018) A panel quantile approach to attrition bias in big data: Evidence from a randomized experiment. Journal of Econometrics 211, 61–82.CrossRefGoogle Scholar
Honda, T., Ing, C.-K., & Wu, W.-Y. (2019) Adaptively weighted group lasso for semiparametric quantile regression models. Bernoulli 25(4B), 3311–3338.CrossRefGoogle Scholar
Horowitz, J.L. & Lee, S. (2005) Nonparametric estimation of an additive quantile regression model. Journal of the American Statistical Association 100(472), 1238–1249.CrossRefGoogle Scholar
Horowitz, J.L. & Spokoiny, V.G. (2002) An adaptive, rate-optimal test of linearity for median regression models. Journal of the American Statistical Association 97(459), 822–835.CrossRefGoogle Scholar
Kai, B., Li, R., & Zou, H. (2011) New efficient estimation and variable selection methods for semiparametric varying-coefficient partially linear models. Annals of Statistics 39, 305–332.CrossRefGoogle ScholarPubMed
Kato, K. (2011) Group Lasso for high dimensional sparse quantile regression models. Preprint, arXiv:1103.1458.Google Scholar
Koenker, R. (2017) Quantile regression: 40 years on. Annual Review of Economics 9, 155–176.CrossRefGoogle Scholar
Koenker, R. & Bassett, G. (1978) Regression quantiles. Econometrica 46, 33–50.CrossRefGoogle Scholar
Koenker, R., Chernozhukov, V., He, X., & Peng, L. (eds.) (2017) Handbook of Quantile Regression. Chapman and Hall/CRC.CrossRefGoogle Scholar
Koenker, R. & Xiao, Z. (2006) Quantile autoregression. Journal of the American Statistical Association 101(475), 980–990.CrossRefGoogle Scholar
Ledoux, M. & Talagrand, M. (2013) Probability in Banach Spaces: Isoperimetry and Processes. Springer Science & Business Media.Google Scholar
Lee, E.R., Noh, H., & Park, B.U. (2014) Model selection via Bayesian information criterion for quantile regression models. Journal of the American Statistical Association 109(505), 216–229.CrossRefGoogle Scholar
Lee, S., Liao, Y., Seo, M.H., & Shin, Y. (2018) Oracle estimation of a change point in high dimensional quantile regression. Journal of the American Statistical Association 43, 1184–1194.CrossRefGoogle Scholar
Li, Y.J. & Zhu, J. (2008) L1-norm quantile regression. Journal of Computational and Graphical Statistics 17, 163–185.CrossRefGoogle Scholar
Linton, O.B. & Whang, Y.-J. (2004). A quantilogram approach to evaluating directional predictability. Available at SSRN 485342.Google Scholar
Loh, P.-L. (2017). Statistical consistency and asymptotic normality for high-dimensional robust $m$ -estimators. Annals of Statistics 45(2), 866–896.CrossRefGoogle Scholar
Loh, P.-L. & Wainwright, M.J. (2012) High-dimensional regression with noisy and missing data: Provable guarantees with nonconvexity. Annals of Statistics 40(3), 1637–1664.CrossRefGoogle Scholar
Loh, P.-L. and Wainwright, M.J. (2015). Regularized $m$ -estimators with nonconvexity: Statistical and algorithmic theory for local optima. Journal of Machine Learning Research 16, 559–616.Google Scholar
Lv, S., Lin, H., Lian, H., & Huang, J. (2018) Oracle inequalities for sparse additive quantile regression in reproducing kernel Hilbert space. Annals of Statistics 46(2), 781–813.CrossRefGoogle Scholar
Mei, S., Bai, Y., & Montanari, A. (2018) The landscape of empirical risk for nonconvex losses. Annals of Statistics 46(6A), 2747–2774.CrossRefGoogle Scholar
Negahban, S.N., Ravikumar, P., Wainwright, M.J., & Yu, B. (2012) A unified framework for high-dimensional analysis of M-estimators with decomposable regularizers. Statistical Science 27(4), 538–557.CrossRefGoogle Scholar
Nolan, J. (2003) Stable Distributions: Models for Heavy-Tailed Data. Birkhauser.CrossRefGoogle Scholar
Park, S., He, X., & Zhou, S. (2017) Dantzig-type penalization for multiple quantile regression with high dimensional covariates. Statistica Sinica 27, 1619–1638.Google Scholar
Raskutti, G., Wainwright, M.J., & Yu, B. (2011) Minimax rates of estimation for high-dimensional linear regression over ${l}_q$ -balls. IEEE Transactions on Information Theory 57(10), 6976–6994.CrossRefGoogle Scholar
Ruppert, D. & Carroll, R.J. (1980) Trimmed least squares estimation in the linear model. Journal of the American Statistical Association 75(372), 828–838.CrossRefGoogle Scholar
Sherwood, B. & Wang, L. (2016) Partially linear additive quantile regression in ultra-high dimension. Annals of Statistics 44(1), 288–317.CrossRefGoogle Scholar
Shows, J.H., Lu, W., & Zhang, H.H. (2010) Sparse estimation and inference for censored median regression. Journal of Statistical Planning and Inference 140, 1903–1917.CrossRefGoogle ScholarPubMed
Su, L. & Hoshino, T. (2016) Sieve instrumental variable quantile regression estimation of functional coefficient models. Journal of Econometrics 191(1), 231–254.CrossRefGoogle Scholar
Tang, Y., Song, X., Wang, H.J., & Zhu, Z. (2013) Variable selection in high-dimensional quantile varying coefficient models. Journal of Multivariate Analysis 122, 115–132.CrossRefGoogle Scholar
Tao, P.D. & An, L. (1997) Convex analysis approach to D.C. programming: Theory, algorithms and applications. Acta Mathematica Vietnamica 22(1), 289–355.Google Scholar
Tibshirani, R. (1996) Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society. Series B 58, 267–288.Google Scholar
van de Geer, S.A. (2000) Empirical Processes in M-Estimation. Cambridge University Press.Google Scholar
van de Geer, S.A. (2016) Estimation and Testing under Sparsity. Springer.CrossRefGoogle Scholar
van der Vaart, A. & Wellner, J. (1996) Weak Convergence and Empirical Processes: With Applications to Statistics. Springer Science & Business Media.CrossRefGoogle Scholar
Wagener, J., Volgushev, S., & Dette, H. (2012) The quantile process under random censoring. Mathematical Methods of Statistics 21, 127–141.CrossRefGoogle Scholar
Wang, H., Li, G., & Jiang, G. (2007) Robust regression shrinkage and consistent variable selection through the LAD-lasso. Journal of Business & Economic Statistics 25, 347–355.CrossRefGoogle Scholar
Wang, H., Zhou, J., & Li, Y. (2013a) Variable selection for censored quantile regression. Statistica Sinica 23, 145–167.Google Scholar
Wang, L. (2013) The L1 penalized LAD estimator for high dimensional linear regression. Journal of Multivariate Analysis 120, 135–151.CrossRefGoogle Scholar
Wang, L. (2019). L1 -regularized quantile regression with many regressors under lean assumptions. University of Minnesota Digital Conservancy. Available at https://hdl.handle.net/11299/202063.Google Scholar
Wang, L., Kim, Y., & Li, R. (2013b) Calibrating non-convex penalized regression in ultra-high dimension. Annals of Statistics 41(5), 2505–2536.CrossRefGoogle ScholarPubMed
Wang, L., Peng, B., Bradic, J., Li, R., & Wu, Y. (2020) A tuning-free robust and efficient approach to high-dimensional regression. Journal of the American Statistical Association 115(532), 1700–1714.CrossRefGoogle Scholar
Wang, L., Wu, Y., & Li, R. (2012) Quantile regression for analyzing heterogeneity in ultra-high dimension. Journal of the American Statistical Association 107(497), 214–222.CrossRefGoogle ScholarPubMed
Wu, Y.C. & Liu, Y.F. (2009) Variable selection in quantile regression. Statistica Sinica 19, 801–817.Google Scholar
Zhang, C.H. (2010) Nearly unbiased variable selection under minimax concave penalty. Annals of Statistics 38, 894–942.CrossRefGoogle Scholar
Zhao, T., Kolar, M., & Liu, H. (2014) A general framework for robust testing and confidence regions in high-dimensional quantile regression. Preprint, arXiv:1412.8724.Google Scholar
Zheng, Q., Peng, L., & He, X. (2015) Globally adaptive quantile regression with ultra-high dimensional data. Annals of Statistics 43(5), 2225–2258.CrossRefGoogle ScholarPubMed
Zhong, W., Zhu, L., Li, R., & Cui, H. (2016) Regularized quantile regression and robust feature screening for single index models. Statistica Sinica 26(1), 69–95.Google ScholarPubMed
Zou, H. & Yuan, M. (2008) Composite quantile regression and the oracle model selection theory. Annals of Statistics 36, 1108–1126.CrossRefGoogle Scholar