Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Taniguchi, Masanobu
1988.
Asymptotic expansions of the distributions of some test statistics for Gaussian ARMA processes.
Journal of Multivariate Analysis,
Vol. 27,
Issue. 2,
p.
494.
TANIGUCHI, MASANOBU
1989.
Multivariate Statistics and Probability.
p.
521.
Taniguchi, Masanobu
and
Maekawa, Koichi
1990.
Asymptotic Expansions of the Distributions of Statistics Related to the Spectral Density Matrix in Multivariate Time Series and Their Applications.
Econometric Theory,
Vol. 6,
Issue. 1,
p.
75.
Taniguchi, Masanobu
1991.
Third-order asymptomic properties of a class of test statistics under a local alternative.
Journal of Multivariate Analysis,
Vol. 37,
Issue. 2,
p.
223.
Zhang, Guoqiang
and
Taniguchi, Masanobu
1994.
DISCRIMINANT ANALYSIS FOR STATIONARY VECTOR TIME SERIES.
Journal of Time Series Analysis,
Vol. 15,
Issue. 1,
p.
117.
Maeyama, Yusuke
Tamaki, Kenichiro
and
Taniguchi, Masanobu
2011.
Preliminary test estimation for spectra.
Statistics & Probability Letters,
Vol. 81,
Issue. 11,
p.
1580.
Xu, Xiaofei
Liu, Yan
and
Taniguchi, Masanobu
2024.
Second-order robustness for time series inference.
Statistical Inference for Stochastic Processes,
Vol. 27,
Issue. 1,
p.
213.


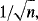 where
where 