Article contents
TARGETING ESTIMATION OF CCC-GARCH MODELS WITH INFINITE FOURTH MOMENTS
Published online by Cambridge University Press: 07 September 2015
Abstract
As an alternative to quasi-maximum likelihood, targeting estimation is a much applied estimation method for univariate and multivariate GARCH models. In terms of variance targeting estimation, recent research has pointed out that at least finite fourth moments of the data generating process is required, if one wants to perform inference in GARCH models by relying on asymptotic normality of the estimator. Such moment conditions may not be satisfied in practice for financial returns, highlighting a potential drawback of variance targeting estimation. In this paper, we consider the large-sample properties of the variance targeting estimator for the multivariate extended constant conditional correlation GARCH model when the distribution of the data generating process has infinite fourth moments. Using nonstandard limit theory, we derive new results for the estimator stating that, under suitable conditions, its limiting distribution is multivariate stable. The rate of consistency of the estimator is slower than 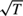 $\sqrt T$ and depends on the tail shape of the data generating process. A simulation study illustrates the derived properties of the targeting estimator.
$\sqrt T$ and depends on the tail shape of the data generating process. A simulation study illustrates the derived properties of the targeting estimator.
- Type
- ARTICLES
- Information
- Copyright
- Copyright © Cambridge University Press 2015
References
REFERENCES
- 11
- Cited by


