Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T16:54:50.234Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE ERROR ACCURATE STATISTIC BASED ON NONPARAMETRIC LIKELIHOOD

Published online by Cambridge University Press:  01 March 2021

Lorenzo Camponovo ,
Yukitoshi Matsushita  and
Taisuke Otsu
Lorenzo Camponovo
Affiliation:
University of Applied Sciences and Arts of Italian Switzerland
Yukitoshi Matsushita
Affiliation:
Hitotsubashi University
Taisuke Otsu*
Affiliation:
London School of Economics
*
Address correspondence to Taisuke Otsu, Department of Economics, London School of Economics, Houghton Street, LondonWC2A 2AE, UK; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper develops a new test statistic for parameters defined by moment conditions that exhibits desirable relative error properties for the approximation of tail area probabilities. Our statistic, called the tilted exponential tilting (TET) statistic, is constructed by estimating certain cumulant generating functions under exponential tilting weights. We show that the asymptotic p-value of the TET statistic can provide an accurate approximation to the p-value of an infeasible saddlepoint statistic, which admits a Lugannani–Rice style adjustment with relative errors of order 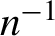$n^{-1}$ both in normal and large deviation regions. Numerical results illustrate the accuracy of the proposed TET statistic. Our results cover both just- and overidentified moment condition models. A limitation of our analysis is that the theoretical approximation results are exclusively for the infeasible saddlepoint statistic, and closeness of the p-values for the infeasible statistic to the ones for the feasible TET statistic is only numerically assessed.

Type
ARTICLES
Information
Econometric Theory , Volume 37 , Issue 6 , December 2021 , pp. 1214 - 1237
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We gratefully acknowledge support from the JSPS KAKENHI (18K01541; Matsushita) and the ERC Consolidator Grant (SNP 615882; Otsu). We would like to thank Elvezio Ronchetti and Richard Spady for their helpful discussions and seminar participants at the University of Geneva for their comments. We would also like to thank the Editor, a Co-Editor, and anonymous referees for their helpful comments.

References

REFERENCES

Almudevar, A., Field, C., & Robinson, J. (2000) The density of multivariate M-estimates. Annals of Statistics 28, 275–297.CrossRefGoogle Scholar
Andrews, D.W.K. & Stock, J.H. (2007) Inference with weak instruments. In Blundell, R., Newey, W., & Persson, T. (eds.), Advances in Economics and Econometrics, Theory and Applications. Ninth World Congress, vol. 3, pp. 122–173. Cambridge University Press.Google Scholar
Baggerly, K.A. (1998) Empirical likelihood as a goodness-of-fit measure. Biometrika 85, 535–547.CrossRefGoogle Scholar
Brown, B.W. & Newey, W.K. (1998) Efficient semiparametric estimation of expectations. Econometrica 66, 453–464.CrossRefGoogle Scholar
Czellar, V. & Ronchetti, E. (2010) Accurate and robust tests for indirect inference. Biometrika 97, 621–630.CrossRefGoogle Scholar
Daniels, H.E. & Young, G.A. (1991) Saddlepoint approximation for the studentized mean, with an application to the bootstrap. Biometrika 78, 169–179.CrossRefGoogle Scholar
DiCiccio, T.J., Hall, P., & Romano, J. (1991) Empirical likelihood is Bartlett-correctable. Annals of Statistics 19, 1053–1061.CrossRefGoogle Scholar
Efron, B. (1981) Nonparametric standard errors and confidence intervals. Canadian Journal of Statistics 9, 139–172.CrossRefGoogle Scholar
Efron, B. (1982) Transformation theory: How normal is a family of distributions? Annals of Statistics 10, 323–339.Google Scholar
Field, C.A. (1982) Small sample asymptotic expansions for multivariate M-estimates. Annals of Statistics 10, 672–689.CrossRefGoogle Scholar
Huber, P.J. & Ronchetti, E.M. (2009) Robust Statistics, 2nd Edition. Wiley.CrossRefGoogle Scholar
Imbens, G.W., Spady, R.H., & Johnson, P. (1998) Information theoretic approaches to inference in moment condition models. Econometrica 66, 333–357.CrossRefGoogle Scholar
Jensen, J.L. (1995) Saddlepoint Approximations. Oxford University Press.Google Scholar
Jensen, J.L. & Wood, A.T.A. (1998) Large deviation and other results for minimum contrast estimators. Annals of the Institute of Mathematical Statistics 50, 673–695.CrossRefGoogle Scholar
Jing, B.Y. & Robinson, J. (1994) Saddlepoint approximations for marginal and conditional probabilities of transformed variables. Annals of Statistics 22, 1115–1132.CrossRefGoogle Scholar
Jing, B.Y., Shao, Q.M., & Zhou, W. (2004) Saddlepoint approximation for student’s t-statistic with no moment conditions. Annals of Statistics 32, 2697–2711.CrossRefGoogle Scholar
Jing, B.Y. & Wood, A.T.A. (1996) Exponential empirical likelihood is not Bartlett correctable. Annals of Statistics 24, 365–369.CrossRefGoogle Scholar
Kitamura, Y. (2007) Empirical likelihood methods in econometrics: Theory and practice. In Blundell, R., Newey, W.K., & Persson, T. (eds.), Advances in Economics and Econometrics, vol. III, pp. 174–237. Cambridge University Press.Google Scholar
Kitamura, Y. & Stutzer, M. (1997) An information-theoretic alternative to generalized method of moments estimation. Econometrica 65, 861–874.CrossRefGoogle Scholar
Kolassa, J. & Robinson, J. (2011) Saddlepoint approximations for likelihood ratio like statistics with applications to permutation tests. Annals of Statistics 39, 3357–3368.CrossRefGoogle Scholar
Ma, Y. & Ronchetti, E. (2011) Saddlepoint test in measurement error models. Journal of the American Statistical Association 106, 147–156.CrossRefGoogle Scholar
Newey, W.K. & Smith, R.J. (2004) Higher order properties of GMM and generalized empirical likelihood estimators. Econometrica 72, 219–255.CrossRefGoogle Scholar
Owen, A.B. (1988) Empirical likelihood ratio confidence intervals for a single functional. Biometrika 75, 237–249.CrossRefGoogle Scholar
Owen, A.B. (2001) Empirical Likelihood. Chapman and Hall.CrossRefGoogle Scholar
Phillips, P.C.B. (1980) The exact distribution of instrumental variable estimators in an equation containing $n+1$ endogenous variables. Econometrica 48, 861–878.CrossRefGoogle Scholar
Phillips, P.C.B. (1984) The exact distribution of LIML: I. International Economic Review 25, 249–261.CrossRefGoogle Scholar
Phillips, P.C.B. (1985) The exact distribution of LIML: II. International Economic Review 26, 21–36.CrossRefGoogle Scholar
Phillips, P.C.B. (1986) The distribution of FIML in the leading case. International Economic Review 27, 239–243.CrossRefGoogle Scholar
Phillips, P.C.B. (1989) Partially identified econometric models. Econometric Theory 5, 181–240.CrossRefGoogle Scholar
Robinson, J., Ronchetti, E., & Young, G.A. (2003) Saddlepoint approximations and tests based on multivariate M-estimates. Annals of Statistics 31, 1154–1169.CrossRefGoogle Scholar
Skovgaard, I.M. (1990) On the density of minimum contrast estimators. Annals of Statistics 18, 779–789.CrossRefGoogle Scholar
Staiger, D. & Stock, J.H. (1997) Instrumental variables regression with weak instruments. Econometrica 65, 557–586.CrossRefGoogle Scholar
Tingley, M.A. & Field, C.A. (1990) Small-sample confidence intervals. Journal of the American Statistical Association 85, 427–434.CrossRefGoogle Scholar