Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-09T06:24:25.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Methods for Constructing Top Order Invariant Polynomials

Published online by Cambridge University Press:  11 February 2009

Yasuko Chikuse
Yasuko Chikuse
Affiliation:
Kagawa University
Get access Rights & Permissions [Opens in a new window]

Abstract

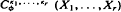The invariant polynomials (Davis [8] and Chikuse [2] with r(r ≥ 2) symmetric matrix arguments have been defined, extending the zonal polynomials, and applied in multivariate distribution theory. The usefulness of the polynomials has attracted the attention of econometricians, and some recent papers have applied the methods to distribution theory in econometrics (e.g., Hillier [14] and Phillips [22]).

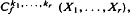The ‘top order’ invariant polynomials , in which each of the partitions of ki 1 = 1,…,r, and 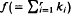has only one part, occur frequently in multivariate distribution theory (e.g., Hillier and Satchell [17] and Phillips [27]). In this paper we give three methods of constructing these polynomials, extending those of Ruben [28] for the top order zonal polynomials. The first two methods yield explicit formulae for the polynomials and then we give a recurrence procedure. It is shown that some of the expansions presented in Chikuse and Davis [4] are simplified for the top order invariant polynomials. A brief discussion is given on the ‘lowest order’ invariant polynomials.

Type
Articles
Information
Econometric Theory , Volume 3 , Issue 2 , April 1987 , pp. 195 - 207
Copyright
Copyright © Cambridge University Press 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Boerner, H.Representations of groups. North-Holland: Amsterdam, 1963.Google Scholar
2.Chikuse, Y. Invariant polynomials with matrix arguments and their applications. In Gupta, R. P. (ed.), Multivariate Statistical Analysis, pp. 53–68. North-Holland: Amsterdam, 1980.Google Scholar
3.Chikuse, Y.Distributions of some matrix variates and latent roots in multivariate Behrens–Fisher discriminant analysis. Annals of Statistics 9 (1981): 401–407.CrossRefGoogle Scholar
4.Chikuse, Y. & Davis, A.W.. Some properties of invariant polynomials with matrix arguments and their applications in econometrics. Annals of the Institute of Statistical Mathematics 38 (1986): 109–122.Google Scholar
5.Chikuse, Y. & Davis, A.W.. A survey on the invariant polynomials with matrix arguments in relation to econometric distribution theory. Econometric Theory 2 (1986): 232–248.CrossRefGoogle Scholar
6.Constantine, A.G.Some noncentral distribution problems in multivariate analysis. Annals of Mathematical Statistics 34 (1963): 1270–1285.Google Scholar
7.Davis, A.W.Invariant polynomials with two matrix arguments, extending the zonal polynomials: Applications to multivariate distribution theory. Annals of the Institute of Statistical Mathematics A31 (1979): 465–485.Google Scholar
8.Davis, A.W. Invariant polynomials with two matrix arguments, extending the zonal polynomials. In Krishnaiah, P.R. (ed.) Multivariate Analysis- V, pp. 287–299. North-Holland: Amsterdam, 1980.Google Scholar
9.Davis, A.W.On the effects of multivariate nonnormality on Wilk's likelihood ratio criterion. Biometrika 67 (1980): 419–427.CrossRefGoogle Scholar
10.Davis, A.W.On the construction of a class of invariant polynomials in several matrices, extending the zonal polynomials. Annals of the Institute of Statistical Mathematics A33 (1981): 297–313.Google Scholar
11.Don, F.J.H.The expectation of products of quadratic forms in normal variables. Statistica Neerlandica 33 (1979): 73–79.Google Scholar
12.Hayakawa, T.Asymptotic distribution of a generalized Hotelling's in the doubly noncentral case. Annals of the Institute of Statistical Mathematics A33 (1981): 15–25.CrossRefGoogle Scholar
13.Hayakawa, T.On some formulas for weighted sum of invariant polynomials of two matrix arguments. Journal of Statistical Planning and Inference 6 (1982): 105–114.Google Scholar
14.Hillier, G.H.On the joint and marginal densities of instrumental variable estimators in a general structural equation. Econometric Theory 1 (1985): 53–72.Google Scholar
15.Hillier, G.H.Marginal densities of instrumental variables estimators: Further exact results. Monash University, Mimeo, 1985.Google Scholar
16.Hillier, G.H., Kinal, T.W. & Srivastava, V.K.. On the moments of ordinary least squares and instrumental variable estimators in a general structural equation. Econometrica 52 (1984): 185–202.CrossRefGoogle Scholar
17.Hillier, G.H. & Satchell, S.E.. Finite sample properties of a two-stage single equation estimator in the SUR model. Econometric Theory 2 (1986): 66–74.CrossRefGoogle Scholar
18.James, A.T.Distributions of matrix variates and latent roots derived from normal samples. Annals of Mathematical Statistics 35 (1964): 475–501.Google Scholar
19.Magnus, J.R.The moments of products of quadratic forms in normal variables. Statistica Neerlandica 32 (1978): 201–210.Google Scholar
20.Magnus, J.R.The expectation of products of quadratic forms in normal variables: The practice. Statistica Neerlandica 33 (1979): 131–136.CrossRefGoogle Scholar
21.Mathai, A.M. & Pillai, K.C.S.. Further results on the trace of a noncentral Wishart matrix. Communications in Statistics: Theory and Methods 11 (1982): 1077–1086.CrossRefGoogle Scholar
22.Phillips, P.C.B.The exact distribution of instrumental variable estimators in an equation containing n + 1 endogeneous variables'. Econometrica 48 (1980): 861–878.CrossRefGoogle Scholar
23.Phillips, P.C.B. The exact distribution of LIML II. Cowles Foundation Discussion Paper No. 663, Yale University, 1983.Google Scholar
24.Phillips, P.C.B.The exact distribution of exogeneous variable coefficient estimators. Journal of Econometrics 26 (1984): 387–398.Google Scholar
25.Phillips, P.C.B. An everywhere convergent series representation of the distribution of Hotelling's generalised . Cowles Foundation Discussion Paper No. 723, Yale University, 1984.Google Scholar
26.Phillips, P.C.B.The exact distribution of the SUR estimator. Econometrica 53 (1985): 745–756.CrossRefGoogle Scholar
27.Phillips, P.C.B.The exact distribution of the Wald statistic. Econometrica 54 (1986): 881–895.Google Scholar
28.Ruben, H.Probability content of regions under spherical normal distributions IV. The dis tribution of homogeneous and nonhomogeneous quadratic forms of normal variables. Annals of Mathematical Statistics 33 (1962): 542–570.Google Scholar
29.Takemura, A.Zonal polynomials. Hayward, California: Institute of Mathematical Statistics, 1984.CrossRefGoogle Scholar
30.Weyl, H.The classical groups, (2nd ed.). Princeton, New Jersey: Princeton University Press, 1946.Google Scholar