Article contents
EFFICIENT TWO-STEP GENERALIZED EMPIRICAL LIKELIHOOD ESTIMATION AND TESTS WITH MARTINGALE DIFFERENCES
Published online by Cambridge University Press: 29 June 2020
Abstract
This paper considers two-step generalized empirical likelihood (GEL) estimation and tests with martingale differences when there is a computationally simple 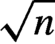 $\sqrt n$-consistent estimator of nuisance parameters or the nuisance parameters can be eliminated with an estimating function of parameters of interest. As an initial estimate might have asymptotic impact on final estimates, we propose general
$\sqrt n$-consistent estimator of nuisance parameters or the nuisance parameters can be eliminated with an estimating function of parameters of interest. As an initial estimate might have asymptotic impact on final estimates, we propose general 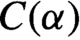 $C(\alpha )$-type transformed moments to eliminate the impact, and use them in the GEL framework to construct estimation and tests robust to initial estimates. This two-step approach can save computational burden as the numbers of moments and parameters are reduced. A properly constructed two-step GEL (TGEL) estimator of parameters of interest is asymptotically as efficient as the corresponding joint GEL estimator. TGEL removes several higher-order bias terms of a corresponding two-step generalized method of moments. Our moment functions at the true parameters are martingales, thus they cover some spatial and time series models. We investigate tests for parameter restrictions in the TGEL framework, which are locally as powerful as those in the joint GEL framework when the two-step estimator is efficient.
$C(\alpha )$-type transformed moments to eliminate the impact, and use them in the GEL framework to construct estimation and tests robust to initial estimates. This two-step approach can save computational burden as the numbers of moments and parameters are reduced. A properly constructed two-step GEL (TGEL) estimator of parameters of interest is asymptotically as efficient as the corresponding joint GEL estimator. TGEL removes several higher-order bias terms of a corresponding two-step generalized method of moments. Our moment functions at the true parameters are martingales, thus they cover some spatial and time series models. We investigate tests for parameter restrictions in the TGEL framework, which are locally as powerful as those in the joint GEL framework when the two-step estimator is efficient.
- Type
- ARTICLES
- Information
- Copyright
- © Cambridge University Press 2020
Footnotes
We are grateful to Co-Editor Patrik Guggenberger and three anonymous referees for their valuable suggestions and comments. Some of issues on testing of hypotheses using a GMM approach with an initial consistent estimate in a two-step estimation framework were posed by Professor Junsen Zhang of the Chinese University of Hong Kong. We appreciate Junsen for bringing some of the testing issues addressed in this paper to our attention. This paper has been presented at SMU and in the Third Guangzhou Econometrics Workshop at the Sun Yat-Sen University, Guangzhou, China. We are grateful to Zhentao Shi, Liangjun Su, Zhenlin Yang, Jun Yu, and other seminar participants for helpful comments. The first author gratefully acknowledges the financial support from the National Natural Science Foundation of China (Nos. 71973030 and 71833004) and Program for Innovative Research Team of Shanghai University of Finance and Economics.
References
- 3
- Cited by


