Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T09:12:46.220Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSISTENCY AND ASYMPTOTIC NORMALITY OF SIEVE ML ESTIMATORS UNDER LOW-LEVEL CONDITIONS

Published online by Cambridge University Press:  11 April 2014

Herman J. Bierens
Herman J. Bierens*
Affiliation:
Pennsylvania State University
*
*Address correspondence to Herman J. Bierens, Professor Emeritus of Economics, Pennsylvania State University, University Park, PA 16802; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers sieve maximum likelihood estimation of seminonparametric (SNP) models with an unknown density function as non-Euclidean parameter, next to a finite-dimensional parameter vector. The density function involved is modeled via an infinite series expansion, so that the actual parameter space is infinite-dimensional. 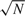It will be shown that under low-level conditions the sieve estimators of these parameters are consistent, and the estimators of the Euclidean parameters are $\sqrt N$ asymptotically normal, given a random sample of size N. The latter result is derived in a different way than in the sieve estimation literature. It appears that this asymptotic normality result is in essence the same as for the finite dimensional case. This approach is motivated and illustrated by an SNP discrete choice model.

Type
ARTICLES
Information
Econometric Theory , Volume 30 , Issue 5 , October 2014 , pp. 1021 - 1076
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ackerberg, D., Chen, X., & Hahn, J. (2012) A practical asymptotic variance estimator for two-step semiparametric estimators. Review of Economics and Statistics 94, 482–498.CrossRefGoogle Scholar
Ai, C. & Chen, X. (2007) Estimation of possibly misspecified semiparametric conditional moment restriction models with different conditioning variables. Journal of Econometrics 141,5–43.Google Scholar
Andrews, D.W.K. (1994) Asymptotics for semiparametric econometric models via stochastic equicontinuity. Econometrica 62, 43–72.Google Scholar
Bahadur, R.R. (1967) Rates of convergence of estimates and test statistics. Annals of Mathematical Statistics 38, 303–324.Google Scholar
Bickel, P.J., Klaassen, C.A.J., Ritov, Y., & Wellner, J.A. (1998) Efficient and Adaptive Estimation for Semiparametric Models. Springer.Google Scholar
Bierens, H.J. (2004) Introduction to the Mathematical and Statistical Foundations of Econometrics. Cambridge University Press.Google Scholar
Bierens, H.J. (2008) Semi-nonparametric interval-censored mixed proportional hazard models: Identification and consistency results. Econometric Theory 24, 749–794.Google Scholar
Bierens, H.J. (2013) Supplement to: Consistency and asymptotic normality of sieve ML estimators under low-level conditions. http://econ.la.psu.edu/∼hbierens/SNPMODELS_A.PDF Google Scholar
Bierens, H.J. (2014) The Hilbert space theoretical foundation of semi-nonparametric modeling. In Racine, J., Su, L., & Ullah, A. (eds.), Oxford Handbook of Applied Nonparametric and Semiparametric Econometrics and Statistics, Ch. 1. Oxford University Press, 3–37.Google Scholar
Bierens, H.J. & Carvalho, J.R. (2007) Semi-nonparametric competing risks analysis of recidivism. Journal of Applied Econometrics 22, 971–993.Google Scholar
Bierens, H.J. & Song, H. (2013) Semi-nonparametric Modeling and Estimation of First-Price Auctions Models with Auction-Specific Heterogeneity. Working paper, Penn State University. http://econ.la.psu.edu/∼hbierens/AUCTIONS_HETERO.PDF Google Scholar
Bierens, H.J. & Wang, L. (2012) Integrated conditional moment tests for parametric conditional distributions. Econometric Theory 28, 328–362.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley.Google Scholar
Chen, X. (2007) Large sample sieve estimation of semi-nonparametric models. In Heckman, J. & Leamer, E. (eds.), Handbook of Econometrics, vol. 6B, Ch. 76. Elsevier, 5549–5632.Google Scholar
Chen, X. (2011) Penalized Sieve Estimation and Inference of Semi-nonparametric Dynamic Models: A Selective Review. Cowles Foundation Discussion paper no. 2804, Yale University.Google Scholar
Chen, X., Fan, Y., & Tsyrennikov, V. (2006) Efficient estimation of semiparametric multivariate copula models. Journal of the American Statistical Association 101, 1228–1240.Google Scholar
Chen, X. & Shen, X. (1998) Sieve extremum estimates for weakly dependent data. Econometrica 66, 289–314.Google Scholar
Chen, X., Linton, O., & Van Keilegom, I. (2003) Estimation of semiparametric models when the criterion function is not smooth. Econometrica 71, 1591–1608.Google Scholar
Cosslett, S.R. (1983) Distribution-free maximum likelihood estimator of the binary choice model. Econometrica 51, 765–782.Google Scholar
Eastwood, B.J. & Gallant, A.R. (1991) Adaptive rules for semi-nonparametric estimators that achieve asymptotic normality. Econometric Theory 7, 307–340.Google Scholar
Elbers, C. & Ridder, G. (1982) True and spurious duration dependence: The identifiability of the proportional hazard model.Review of Economic Studies 49, 403–409.Google Scholar
Gabler, S., Laisney, F., & Lechner, M. (1993) Seminonparametric estimation of binary-choice models with an application to labor-force participation. Journal of Business & Economic Statistics 11,61–80.Google Scholar
Gallant, A.R. (1981) On the bias in flexible functional forms and an essentially unbiased form: The Fourier flexible form. Journal of Econometrics 15, 211–245.CrossRefGoogle Scholar
Gallant, A.R. & Nychka, D.W. (1987) Semi-nonparametric maximum likelihood estimation. Econometrica 55, 363–390.Google Scholar
Geman, S. & Hwang, C. (1982) Nonparametric maximum likelihood estimation by the method of sieves. Annals of Statistics 10, 401–414.Google Scholar
Gill, R.D. (1989) Non- and semi-parametric maximum likelihood estimators and the von Mises method (Part 1). Scandinavian Journal of Statistics 16, 97–128.Google Scholar
Grenander, U. (1981) Abstract Inference. Wiley.Google Scholar
Hahn, J. (1994) The efficiency bound of the mixed proportional hazard model. Review of Economic Studies 61, 607–629.Google Scholar
Hannan, E.J. & Quinn, B.G. (1979) The determination of the order of an autoregression. Journal of the Royal Statistical Society, Series B 41, 190–195.Google Scholar
Heckman, J.J. (1979) Sample selection bias as a specification error. Econometrica 47, 153–161.CrossRefGoogle Scholar
Heckman, J.J. & Singer, B. (1984) A method for minimizing the impact of distributional assumptions in econometric models for duration data. Econometrica 52, 271–320.Google Scholar
Horowitz, J.L. (1992) A smoothed maximum score estimator for the binary response model. Econometrica 60, 505–531.CrossRefGoogle Scholar
Horowitz, J.L. (1998) Semiparametric Methods in Econometrics. Springer.Google Scholar
Ichimura, H. (1993) Semiparametric least squares and weighted SLS estimation of single-index models. Journal of Econometrics 58, 71–120.Google Scholar
Ichimura, H. & Lee, S. (2010) Characterization of the asymptotic distribution of semiparametric M-estimators. Journal of Econometrics 159, 252–266.Google Scholar
Jennrich, R.I. (1969) Asymptotic properties of nonlinear least squares estimators.Annals of Mathematical Statistics 40, 633–643.Google Scholar
Khan, S. (2013) Distribution free estimation of heteroskedastic binary response models using Probit/Logit criterion functions. Journal of Econometrics 172, 168–182.CrossRefGoogle Scholar
Klein, R.W. & Spady, R.H. (1993) An efficient semiparametric estimator for binary response models. Econometrica 61, 387–421.CrossRefGoogle Scholar
Kronmal, R. & Tarter, M. (1968) The estimation of densities and cumulatives by Fourier series methods. Journal of the American Statistical Association 63, 925–952.Google Scholar
Lancaster, T. (1979) Econometric methods for the duration of unemployment. Econometrica 47, 939–956.Google Scholar
Manski, C.F. (1985) Semiparametric analysis of discrete response: Asymptotic properties of the maximum score estimator. Journal of Econometrics 27, 313–333.CrossRefGoogle Scholar
Manski, C.F. (1988) Identification of binary response models. Journal of the American Statistical Association 83, 729–738.Google Scholar
McLeish, D.L. (1974) Dependent central limit theorems and invariance principles. Annals of Probability 2, 620–628.Google Scholar
Newey, W.K. (1990) Semiparametric efficiency bounds. Journal of Applied Econometrics 5, 99–135.Google Scholar
Newey, W.K. (1994) The asymptotic variance of semiparametric estimators. Econometrica 62, 1349–1382.Google Scholar
Newey, W.K. (1997) Convergence rates and asymptotic normality for series estimators. Journal of Econometrics 79, 147–168.Google Scholar
Ridder, G. & Woutersen, T. (2003) The singularity of the efficiency bound of the mixed proportional hazard model. Econometrica 71, 1579–1589.Google Scholar
Schwarz, G. (1978) Estimating the dimension of a model. Annals of Statistics 6, 461–464.Google Scholar
Shen, X. (1997) On the method of sieves and penalization. Annals of Statistics 25, 2555–2591.Google Scholar
Sims, C.A. (1971) Distributed lag estimation when the parameter space is explicitly infinite-dimensional. Annals of Mathematical Statistics 42, 1622–1636.Google Scholar
Stewart, M.B. (2004) Semi-nonparametric estimation of extended ordered Probit models. The Stata Journal 4, 27–39.CrossRefGoogle Scholar
van der Vaart, A.W. (1998) Asymptotic Statistics. Cambridge University Press.Google Scholar
van der Vaart, A.W. & Wellner, J.A. (1996) Weak Convergence and Empirical Processes. Springer.Google Scholar
Wald, A. (1949) Note on the consistency of the maximum likelihood estimate. Annals of Mathematical Statistics 20, 595–601.CrossRefGoogle Scholar
White, H. & Wooldridge, J. (1991) Some results on sieve estimation with dependent observations. In Barnett, W.A., Powell, J., & Tauchen, G. (eds.), Non-parametric and Semi-parametric Methods in Econometrics and Statistics, Ch. 18. Cambridge University Press, 459–493.Google Scholar
Supplementary material: PDF

Bierens Supplementary Material

Supplementary Material

Download Bierens Supplementary Material(PDF)
PDF 290.2 KB