Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T14:52:50.818Z Has data issue: false hasContentIssue false
  • English
  • Français

BOOTSTRAP INFERENCE FOR MULTIPLE CHANGE-POINTS IN TIME SERIES

Published online by Cambridge University Press:  25 June 2021

Wai Leong Ng ,
Shenyi Pan  and
Chun Yip Yau
Wai Leong Ng*
Affiliation:
The Hang Seng University of Hong Kong
Shenyi Pan
Affiliation:
The University of British Columbia
Chun Yip Yau
Affiliation:
The Chinese University of Hong Kong
*
Address correspondence to Wai Leong Ng, Department of Mathematics, Statistics and Insurance, School of Decision Sciences, The Hang Seng University of Hong Kong, Shatin, NT, Hong Kong; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we propose two bootstrap procedures, namely parametric and block bootstrap, to approximate the finite sample distribution of change-point estimators for piecewise stationary time series. The bootstrap procedures are then used to develop a generalized likelihood ratio scan method (GLRSM) for multiple change-point inference in piecewise stationary time series, which estimates the number and locations of change-points and provides a confidence interval for each change-point. The computational complexity of using GLRSM for multiple change-point detection is as low as 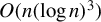$O(n(\log n)^{3})$ for a series of length n. Extensive simulation studies are provided to demonstrate the effectiveness of the proposed methodology under different scenarios. Applications to financial time series are also illustrated.

Type
ARTICLES
Information
Econometric Theory , Volume 38 , Issue 4 , August 2022 , pp. 752 - 792
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We would like to thank the Editor Peter C.B. Phillips, Co-Editor Robert Taylor, and two anonymous referees for their helpful comments and thoughtful suggestions, which led to a much improved version of this paper. This research has been supported in part by HKSAR-RGC-FDS Project No. UGC/FDS14/P01/20 (Ng), and HKSAR-RGC-GRF Nos 14302719, 14305517, 14308218 and 14601015 (Yau).

References

REFERENCES

Antoch, J. & Hušková, M. (1999) Estimators of changes. In Gosh, S. (ed.), Asymptotics, Nonparametrics, and Time Series, pp. 533–578. Marcel Dekker.Google Scholar
Antoch, J., Hušková, M., & Prášková, Z. (1997) Effect of dependence on statistics for determination of change. Journal of Statistical Planning and Inference 60(2), 291–310.CrossRefGoogle Scholar
Antoch, J., Hušková, M., & Veraverbeke, N. (1995) Change-point problem and bootstrap. Journal of Nonparametric Statistics 5(2), 123–144.CrossRefGoogle Scholar
Bai, J. (1995) Least absolute deviation estimation of a shift. Econometric Theory 11(3), 403–436.CrossRefGoogle Scholar
Bai, J., Lumsdaine, R. L., & Stock, J. H. (1998) Testing for and dating common breaks in multivariate time series. The Review of Economic Studies 65(3), 395–432.CrossRefGoogle Scholar
Bhattacharya, P. K. & Brockwell, P. J. (1976) The minimum of an additive process with applications to signal estimation and storage theory. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 37(1), 51–75.CrossRefGoogle Scholar
Billingsley, P. (1999) Convergence of Probability Measures. Wiley.CrossRefGoogle Scholar
Braun, J. V., Braun, R. K., & Müller, H. G. (2000) Multiple changepoint fitting via quasilikelihood, with application to DNA sequence segmentation. Biometrika 87(2), 301–314.CrossRefGoogle Scholar
Cho, H. & Fryzlewicz, P. (2012) Multiscale and multilevel technique for consistent segmentation of nonstationary time series. Statistica Sinica 22(1), 207–229.CrossRefGoogle Scholar
Csörgö, M. & Horváth, L. (1997) Limit Theorems in Change-Point Analysis. Wiley.Google Scholar
Davis, R. A., Lee, T. C. M., & Rodriguez-Yam, G. A. (2006) Structural break estimation for nonstationary time series models. Journal of the American Statistical Association 101(473), 223–239.CrossRefGoogle Scholar
Davis, R. A., Lee, T. C. M., & Rodriguez-Yam, G. A. (2008) Break detection for a class of nonlinear time series models. Journal of Time Series Analysis 29(5), 834–867.CrossRefGoogle Scholar
Davis, R. A. & Yau, C. Y. (2013) Consistency of minimum description length model selection for piecewise stationary time series models. Electronic Journal of Statistics 7, 381–411.CrossRefGoogle Scholar
Dümbgen, L. (1991) The asymptotic behavior of some nonparametric change-point estimators. Annals of Statistics 19(3), 1471–1495.CrossRefGoogle Scholar
Eichinger, B. & Kirch, C. (2018) A MOSUM procedure for the estimation of multiple random change points. Bernoulli 24(1), 526–564.CrossRefGoogle Scholar
Fearnhead, P. & Rigaill, G. (2019) Changepoint detection in the presence of outliers. Journal of the American Statistical Association 114(525), 169–183.CrossRefGoogle Scholar
Fryzlewicz, P. & Subba Rao, S. (2014) Multiple-change-point detection for auto-regressive conditional heteroscedastic processes. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 76(5), 903–924.CrossRefGoogle Scholar
Hinkley, D. V. (1970) Inference about the change-point in a sequence of random variables. Biometrika 57(1), 1–17.CrossRefGoogle Scholar
Hušková, M. & Kirch, C. (2008) Bootstrapping confidence intervals for the change-point of time series. Journal of Time Series Analysis 29(6), 947–972.CrossRefGoogle Scholar
Jackson, B., Scargle, J. D., Barnes, D., Arabhi, S., Alt, A., Gioumousis, P., Gwin, E., Sangtrakulcharoen, P., Tan, L., & Tsai, T. T. (2005) An algorithm for optimal partitioning of data on an interval. IEEE Signal Processing Letters 12(2), 105–108.CrossRefGoogle Scholar
Jennrich, R. I. (1969) Asymptotic properties of non-linear least squares estimators. The Annals of Mathematical Statistics 40(2), 633–643.CrossRefGoogle Scholar
Jiang, L., Wang, X., & Yu, J. (2018) New distribution theory for the estimation of structural break point in mean. Journal of Econometrics 205(1), 156–176.CrossRefGoogle Scholar
Jiang, L., Wang, X., & Yu, J. (2021) In-fill asymptotic theory for structural break point in autoregressions. Econometric Reviews 40(4), 359–386.CrossRefGoogle Scholar
Killick, R., Fearnhead, P., & Eckley, I. A. (2012) Optimal detection of changepoints with a linear computational cost. Journal of the American Statistical Association 107(500), 1590–1598.CrossRefGoogle Scholar
Last, M. & Shumway, R. (2008) Detecting abrupt changes in a piecewise locally stationary time series. Journal of Multivariate Analysis 99(2), 191–214.CrossRefGoogle Scholar
Lavielle, M. & Moulines, E. (2000) Least-squares estimation of an unknown number of shifts in a time series. Journal of Time Series Analysis 21(1), 33–59.CrossRefGoogle Scholar
Lesigne, E. & Volný, D. (2001) Large deviations for martingales. Stochastic Processes and Their Applications 96(1), 143–159.CrossRefGoogle Scholar
Ling, S. (2016) Estimation of change-points in linear and nonlinear time series models. Econometric Theory 32(2), 402–430.CrossRefGoogle Scholar
Messer, M., Albert, S., & Schneider, G. (2018) The multiple filter test for change point detection in time series. Metrika 81(6), 589–607.CrossRefGoogle Scholar
Ombao, H. C., Raz, J. A., von Sachs, R., & Malow, B. A. (2001) Automatic statistical analysis of bivariate nonstationary time series. Journal of the American Statistical Association 96(454), 543–560.CrossRefGoogle Scholar
Picard, D. (1985) Testing and estimating change-points in time series. Advances in Applied Probability 17(4), 841–867.CrossRefGoogle Scholar
Preuss, P., Puchstein, R., & Dette, H. (2015) Detection of multiple structural breaks in multivariate time series. Journal of the American Statistical Association 110(510), 654–668.CrossRefGoogle Scholar
Yao, Y. C. (1987) Approximating the distribution of the maximum likelihood estimate of the change-point in a sequence of independent random variables. Annals of Statistics 15(3), 1321–1328.CrossRefGoogle Scholar
Yao, Y. C. & Au, S. T. (1989) Least-squares estimation of a step function. Sankhyā: The Indian Journal of Statistics, Series A 51(3), 370–381.Google Scholar
Yau, C. Y. & Zhao, Z. (2016) Inference for multiple change points in time series via likelihood ratio scan statistics. Journal of the Royal Statistical Society: Series B 78(4), 895–916.CrossRefGoogle Scholar