Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T05:30:37.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Submatrix Constrained Inverse Eigenvalue Problem involving Generalised Centrohermitian Matrices in Vibrating Structural Model Correction

Part of: Basic linear algebra Numerical linear algebra

Published online by Cambridge University Press:  27 January 2016

Wei-Ru Xu  and
Guo-Liang Chen
Wei-Ru Xu
Affiliation:
Department of Mathematics, Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, East China Normal University, Shanghai, 200241, P. R. China
Guo-Liang Chen*
Affiliation:
Department of Mathematics, Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, East China Normal University, Shanghai, 200241, P. R. China
*
*Corresponding author. Email addresses:[email protected] (W.-R. Xu), [email protected] (G.-L. Chen)
Get access

Abstract

Generalised centrohermitian and skew-centrohermitian matrices arise in a variety of applications in different fields. Based on the vibrating structure equation 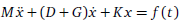where M, D, G, K are given matrices with appropriate sizes and x is a column vector, we design a new vibrating structure mode. This mode can be discretised as the left and right inverse eigenvalue problem of a certain structured matrix. When the structured matrix is generalised centrohermitian, we discuss its left and right inverse eigenvalue problem with a submatrix constraint, and then get necessary and sufficient conditions such that the problem is solvable. A general representation of the solutions is presented, and an analytical expression for the solution of the optimal approximation problem in the Frobenius norm is obtained. Finally, the corresponding algorithm to compute the unique optimal approximate solution is presented, and we provide an illustrative numerical example.

Keywords

Left and right inverse eigenvalue problemoptimal approximation problemgeneralised centrohermitian matrixsubmatrix constraint

MSC classification

Secondary: 65F18: Inverse eigenvalue problems 15A18: Eigenvalues, singular values, and eigenvectors 15A12: Conditioning of matrices
Type
Research Article
Information
East Asian Journal on Applied Mathematics , Volume 6 , Issue 1 , February 2016 , pp. 42 - 59
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bai, Z.-J., The inverse eigenproblem of centrosymmetric matrices with a submatrix constraint and its approximation, SIAM J. Matrix Anal. Appl. 26, 1100–1114 (2005).Google Scholar
[2]Bai, Z.-J. and Chan, R.H., Inverse eigenproblem for centrosymmetric and centroskew matrices and their approximation, Theor. Comput. Sci. 315, 309–318 (2004).CrossRefGoogle Scholar
[3]Baruch, M., Optimization procedure to correct stiffness and flexibility matrices using vibration tests, AIAA J. 16, 1208–1210 (1978).CrossRefGoogle Scholar
[4]Berman, A., Mass matrix correction using an imcomplete set of measured modes, AIAA J. 17, 1147–1148 (1979).Google Scholar
[5]Cantoni, A. and Butler, E., Eigenvalues and eigenvectors of symmetric centrosymmetric matrices, Linear Algebra Appl. 13, 275–288 (1976).CrossRefGoogle Scholar
[6]Chang, X. and Wang, J., The symmetric solution of the matrix equations AX + YA = C, AXAT + BY BT = C, and (ATXA, BTXB) = (C, D), Linear Algebra Appl. 179, 171–189 (1993).CrossRefGoogle Scholar
[7]Chen, W., Wang, X. and Zhong, T., The structure of weighting coefficient matrices of harmonic differential quadrature and its application, Comm. Numer. Methods Eng. 12, 455–460 (1996).Google Scholar
[8]Chu, M.T. and Golub, G.H., Inverse Eigenvalue Problems: Theory, Algorithms, and Application, Oxford Science Publications, Oxford University Press (2005).Google Scholar
[9]Collar, A., On centrosymmetric and centroskew matrices, Quart. J. Mech. Appl. Math. 15, 265–281 (1962).Google Scholar
[10]Datta, L. and Morgera, S., On the reducibility of centrosymmetric matrices-applications in engineering problems, Circuits Systems Signal Process. 8, 71–96 (1989).Google Scholar
[11]Delmas, J., On adaptive EVD asymptotic distribution of centro-symmetric covariance matrices, IEEE Trans. Signal Process. 47, 1402–1406 (1999).Google Scholar
[12]Griswold, N. and Davila, J., Fast algorithm for least squares 2D linear-phase FIR filter design, IEEE Internat. Conf. Acoustics, Speech, Signal Process. 6, 3809–3812 (2001).Google Scholar
[13]Joseph, K.-T., Inverse eigenvalue problem in structure design, AIAA J. 10, 2890–2896 (1992).Google Scholar
[14]Liang, M.-L. and Dai, L.-F., The left and right inverse eigenvalue problems of generalized reflexive and anti-reflexive matrices, J. Comput. Appl. Math. 234, 743–749 (2010).Google Scholar
[15]Liu, Z. and Faßbender, H., An inverse eigenvalue problem and an associated approximation problem for generalized K-centrohermitian matrices, J. Comput. Appl. Math. 206, 578–585 (2007).Google Scholar
[16]Paige, C.C. and Saunders, M.A., Towards a generalized singular value decomposition, SIAM J. Numer. Anal. 18, 398–405 (1981).Google Scholar
[17]Tao, D. and Yasuda, M., A spectral characterization of generalized real symmetric centrosymmetric and generalized real symmetric skew-centrosymmetric matrices, SIAM J. Matrix Anal. Appl. 23, 885–895 (2002).Google Scholar
[18]Weaver, J., Centrosymmetric (cross-symmetric) matrices, their basic properties, eigenvalues, and eigenvectors, Amer. Math. Monthly 92, 711–717 (1985).Google Scholar
[19]Wilkinson, J.H., The Algebraic Eigenvalue Problem, Oxford University Press, Oxford (1988).Google Scholar
[20]Xie, D., Hu, X. and Sheng, Y., The solvability conditions for the inverse eigenproblems of symmetric and generalized centro-symmetric matrices and their approximations, Linear Algebra Appl. 418, 142–152 (2006).Google Scholar
[21]Yasuda, M., Spectral characterizations for hermitian centrosymmetric K-matrices and hermitian skew-centrosymmetric K-matrices, SIAM J. Matrix Anal. Appl. 25, 601–605 (2003).CrossRefGoogle Scholar
[22]Yin, F., Guo, K., Huang, G. and Huang, B., The inverse eigenproblem with a submatrix constraint and the associated approximation problem for (R, S)-symmetric matrices, J. Comput. Appl. Math. 268, 23–33 (2014).Google Scholar
[23]Yin, F. and Huang, G.-X., Left and right inverse eigenvalue problem of (R,S)-symmetric matrices and its optimal approximation problem, Appl. Math. Comput. 219, 9261–9269 (2013).Google Scholar
[24]Zhou, F.-Z., Hu, X.-Y., Zhang, L., The solvability conditions for the inverse eigenvalue problem of centro-symmetric matrices, Linear Algebra Appl. 364, 147–160 (2003).Google Scholar