Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T06:39:05.383Z Has data issue: false hasContentIssue false
  • English
  • Français

XXXI.—On the Dynamical Theory of Heat. Part V. On the Quantities of Mechanical Energy contained in a Fluid in Different States, as to Temperature and Density*

Published online by Cambridge University Press:  17 January 2013

William Thomson
William Thomson
Affiliation:
Professor of Natural Philosophy in the University of Glasgow.
Get access Rights & Permissions [Opens in a new window]

Extract

81. A body which is either emitting heat, or altering its dimensions against resisting forces, is doing work upon matter external to it. The mechanical effect of this work, in one case, is the excitation of thermal motions, and in the other, the overcoming of resistances. The body must itself be altering in its circumstances, so as to contain a less store of work within it, by an amount precisely equal to the aggregate value of the mechanical effects produced: and conversely, the aggregate value of the mechanical effects produced, must depend solely on the initial and final states of the body, and is therefore the same, whatever be the intermediate states through which the body passes, provided the initial and final states be the same.

Type
Research Article
Information
Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 20 , Issue 3 , 1853 , pp. 475 - 482
Copyright
Copyright © Royal Society of Edinburgh 1853

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 478 note * The same notation is used here, as formerly in § 54, viz. p is the pressure of saturated vapour at the temperature t, γ the volume, and L the latent heat of a pound of the vapour, λ the volume of a pound of liquid water, and c the mean thermal capacity of a pound of water between the temperatures 0 and t. A mass weighing a pound, and occupying the volume v, when at the temperature t, must consist of a weight 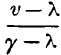of vapour, and 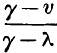of water.

page 482 note * If the values of μ I have used formerly be correct, tʹ would be less than t, for all cases in which t is lower than about 30° cent.; but on the contrary, if t be considerably above 30° cent.,tʹ would be found to exceed t. (See Account of Carnot's Theory, Appendix II.) It may be shewn, that if they are correct, air at the temperature 0° forced up with a pressure of ten atmospheres towards a small orifice, and expanding through it to the atmospheric pressure, would go down in temperature by about 4°·4; but that if it had the temperature of 100° in approaching the orifice, it would leave at a temperature about 5°·2 higher; provided that in each case there is no appreciable expenditure of mechanical energy on sound.