1. The mathematical work of the present paper has been performed to illustrate the hypothesis, that space is continuously occupied by an incompressible frictionless liquid acted on by no force, and that material phenomena of every kind depend solely on motions created in this liquid. But I take, in the first place, as subject of investigation, a finite mass of incompressible frictionless fluid completely enclosed in a rigid fixed boundary.
page 217 note * A frictionless fluid is defined as a mass continuously occupying space, whose contiguous portions press on one another everywhere exactly in the direction perpendicular to the surface separating them.
page 217 note † Helmholtz, —Ueber Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen: Crelle (1858)Google Scholar; translated by Tait, in Phil. Mag. 1867, i.Google ScholarRiemann, —Lehrsätze aus der Analysis situs, &c. Crelle (1857)Google Scholar. See also § 58, below.
page 218 note * I shall use the word contrary to designate merely directional opposition; and reserve the unqualified word opposite, to signify contrary and in one line.
page 220 note * This proposition was, I believe, first proved by Stokes in his paper “On the Friction of Fluids in Motion, and the Equilibrium and Motion of Elastic Solids.”—“Cambridge Philosophical Transactions,” 14th April 1845.Google Scholar
page 223 note * By ∇2 we sball always understand ![]()
page 223 note † This follows, of course, from the known analytical theorem that the operations ∇2 and ![]() are commutative, which is proved thus:—
are commutative, which is proved thus:—
By differentiation we have

and therefore, since 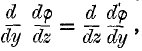

φ being any function whatever. Hence, if ∇2 φ = 0 we have

page 225 note * There is no term ![]() because this would give, in the integral of flow across the whole spherical surface, a finite amount of flow out of or into the space within, implying a generation or destruction of matter.
because this would give, in the integral of flow across the whole spherical surface, a finite amount of flow out of or into the space within, implying a generation or destruction of matter.
page 231 note * The process here described leads merely to the equation obtained by taking the last two equal members of App. A (1) (Thomson & Tait) for the case α = 1, U = φ, U′ = x.
page 232 note * Trans. R. S. Lond., 1851; or “Thomson's, Electrical Papers.” Macmillan. 1869.Google Scholar
page 233 note * Théorie de la Chaleur, § 60.
page 233 note † Essay on Electricity and Magnetism.
page 235 note * Thomson, , Camb. and Dub. Math. Journal, 1849Google Scholar; Liouville's Journal, 1845 and 1847; or Reprints of Electrical Papers, (Macmillan, 1869.)
page 236 note * This is verified synthetically with ease, by direct integrations showing (whether by Cartesian or polar plane co-ordinates), that
And taking ![]() of this, we have
of this, we have

the synthesis of (12).
page 244 note * A finite length of tube with its ends done away by uniting them together.
page 245 note * This theorem (not hitherto published?) will be given in the second volume of Thomson and Tait's “Natural Philosophy.” It may be proved analytically from the general equations of the motion of a particle along a varying guide-curve (Walton, , “Cambridge Mathematical Journal,” 1842, February)Google Scholar; or more synthetically, thus—Let l, m, n be the direction cosines of PT, the tangent to the guide at the point through which the particle is passing at any instant; (x, y, z) the co-ordinates of this point, and ![]() its component velocities parallel to fixed rectangular axes.
its component velocities parallel to fixed rectangular axes.
We have
and from this
But it is readily proved (Thomson and Tait's “Natural Philosophy, § 9, to be made more explicit on this point in a second edition) that the angular velocity with which PT changes direction is equal to ![]() and, if this be denoted by ω, that
and, if this be denoted by ω, that
are the direction cosines of the line PK, perpendicular to PT in the plane in which PT changes direction, and on the side towards which it turns. Hence,
if κ denote the component velocity of P along PK. Now, if the curve were fixed we should have ![]() by the kinematic definition of curvature (Thomson and Tait, § 5); and the plane in which PT changes direction would be the plane of curvature. But in the case actually supposed, there is also in this plane an additional angular velocity equal to
by the kinematic definition of curvature (Thomson and Tait, § 5); and the plane in which PT changes direction would be the plane of curvature. But in the case actually supposed, there is also in this plane an additional angular velocity equal to ![]() and a component angular velocity in the plane of PT and η, equal to
and a component angular velocity in the plane of PT and η, equal to ![]() due to the normal motion of the varying curve. Hence the whole angular velocity ω is the resultant of two components,
due to the normal motion of the varying curve. Hence the whole angular velocity ω is the resultant of two components,

and
![]() in the plane of η.
in the plane of η.
Hence ![]()
and the formula (1) of the text is proved.
page 247 note * Equation (6), from which, as we have seen, that proposition follows immediately, may be proved with greater ease, and not merely for an incompressible fluid, but for any fluid in which the density is a function of the pressure, by the method of rectilineal rectangular co-ordinates from the ordinary hydrokinetic equations. These equations are—
if ![]() denote rate of variation per unit of time, of any function depending on a point or points moving with the fluid; and
denote rate of variation per unit of time, of any function depending on a point or points moving with the fluid; and ![]() denoting density. In terms of rectangular rectilineal co-ordinates we have
denoting density. In terms of rectangular rectilineal co-ordinates we have
Hence
Now
These and the kinetic equations reduce the preceding to

whence, by Σ integration, equation (6) generalised to apply to compressible fluids.
page 251 note * Vortex tubes apparently ending in the fluid, for instance, a portion of fluid bounded by a figure of revolution, revolving round its axis as a solid, constitute no exception. Each infinitesimal vortex tube in this case is completed by a strip of vortex sheet and so is endless.
page 252 note * But without this conception we can make no use of the theory of multiple continuity in hydrokinetics (see §§ 61–63), and Helmholtz's definition is, therefore, perhaps preferable after all to that which I have substituted for it. Mr Clerk Maxwell tells me that J. B. Listing has more recently treated the subject of multiple continuity in a very complete manner in an article entitled “Der Census räumlicher Complexe.”—Königl. Ges. Göttingen, 1861. See also Prof.Cayley, “On the Partition of a Close.”—Phil. Mag. 1861.CrossRefGoogle Scholar