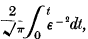 with Extended Tables of Values
with Extended Tables of ValuesPublished online by Cambridge University Press: 06 July 2012
1. The integral 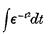 occurs so frequently in various branches of research that, as far back as 1783, Laplace suggested that it would be useful to tabulate its values for successive ranges of integration. It is employed in investigations on the theories of refraction, conduction of heat, of errors of observation, of probabilities, etc. These are familiar to physicists and need not be dwelt upon.
occurs so frequently in various branches of research that, as far back as 1783, Laplace suggested that it would be useful to tabulate its values for successive ranges of integration. It is employed in investigations on the theories of refraction, conduction of heat, of errors of observation, of probabilities, etc. These are familiar to physicists and need not be dwelt upon.
page 257 note * Histoire de l'Acad. Roy. des Sciences, 1783, p. 434; conf. Todhunter, Hist, of the Theory of Probabilities, p. 456.
page 257 note † Conf. Glaisher, in Phil. Mag., vol. xlii, (1871), pp. 429–31.
page 257 note ‡ Gauss ascribed this integration to Laplace; Oriani (in Zach's Monatliche Corresp. for March 1810, Bd. xxi, S. 280 f.) pointed out Euler's prior claim, but Gauss did not correct his statement, Theoria Motus Corp. Cœl., art. 177, p. 212, and Werke, Bd. vii, Ss. 233, 280, 289; Davis's transl. of Theor. Mot., pp. 258, 259. Legendre (Exercices de Calcul Intégral (1811), torn, i, p. 301) asserts Euler's discovery, and refers to his paper, “Evolutio formulae integralis ![]() in Novi Commentarii Acad. Scient. Imp. Petropol, tom, xvi, (for 1771) p. 111. Conf. ib., p. 101; and Comment. Acad. Scient. Petrop., torn, v, (for 1730–1731) p. 44; also Euler's letter to Goldbach of 8th Jan. 1730, in Fuss, Correpond. Math, et Phys., tom. i, p. 13.
in Novi Commentarii Acad. Scient. Imp. Petropol, tom, xvi, (for 1771) p. 111. Conf. ib., p. 101; and Comment. Acad. Scient. Petrop., torn, v, (for 1730–1731) p. 44; also Euler's letter to Goldbach of 8th Jan. 1730, in Fuss, Correpond. Math, et Phys., tom. i, p. 13.
page 257 note § This is the form used by Legendre in his “Traité des Intégrales Euléiennes” in Fonctions Elliptiques, etc. tom, ii, pp. 365, 517–524.
page 258 note * Philos. Mag., vol. xlii., 4th. ser. (1871), pp. 296, 297, 421.
page 258 note † Ibid., p. 437. If either is to be called “Error-function,” it would seem to apply rather to H than to G.
page 258 note ‡ Twice, pp. 134, 135.
page 258 note § In March 1816 appeared Gauss' Bestimmung der Genauigkeit der Beobachtungen, in which he employs several of the constants dependent on values of H.—Il'erke, Bd. iv, Ss. 110, 111, 116.
page 259 note * In his Traité des Fonctions Elliptiques et des Integrales Euleriennes, tom, ii, pp. 520, 521.
page 259 note † Op. cit., tom, ii, pp. 517–524. The method explained below (§ 12) is different.
page 259 note ‡ In Encyclopaedia Metropolitana, vol. ii, pp. 359–458. He also gave a short abstract of it in his Differential and Integral Calculus (1842), p. 657.
page 259 note § Vol. xlii, 4th ser., p. 436.
page 259 note || The paper is continued through the vols. for 1834 (Ss. 249–312), 1835 (553–320), and 1836 (253–308). The Table is in the Jahrbuch for 1834, Ss. 305–308.
page 260 note * Berl Astronom. Jahrbuch für 1834, S. 269. Mr J. W. L. Glaisher (Phil. Mag. (1871), vol. xlii, p. 434) remarks that, if Encke's table were derived from Bessel's, it must have been “by interpolation from his second table.” But he overlooks the fact that Bessel's Table II. is only a continuation of Table I., giving the logarithmic values of the multiple of the integral by gt2 from t = l to t=10, with logarithms of t for argument.
page 260 note † Berl. Astron. Jahrb., 1834, Ss. 309–312.
page 261 note * Op. cit., pp. 16, 20, 22–24.
page 261 note † I began by using the value of ![]() given in Shortrede's Logarithmic Tables (1858), p.602, viz., 1·283 791 670 946 99 which is correct only to the tenth place, and therefore could not affect any of the results up to the eleventh place. This was examined later, and the true value of the constant found to be 1·283 791670 955126. Shortrede's logarithm of
given in Shortrede's Logarithmic Tables (1858), p.602, viz., 1·283 791 670 946 99 which is correct only to the tenth place, and therefore could not affect any of the results up to the eleventh place. This was examined later, and the true value of the constant found to be 1·283 791670 955126. Shortrede's logarithm of ![]() is correct. His value of sin 1° is also in error after the tenth decimal.
is correct. His value of sin 1° is also in error after the tenth decimal.
page 261 note ‡ In the small table given by Airy, Theory of Errors, p. 24, six of the constants dependent on P are in error in the 5th and 6th places, three of them in the 4th.
page 261 note § Théorie Analytique des Probabilités, 2e. ed. (1814), p. 103, and Mécanique Céleste, liv. x, c. i, sec. 5.
page 262 note * Conf. Hymers’ Integ. Calc., pp. 123, 151.
page 263 note * See Laplace's Méc. Cél., ut sup., and Theor. Anal des Probab., p. 104; De Morgan, “Theory of Probabilities, § 63; and Diff. and Integ. Calc., p. 591.
page 265 note * In the example above of t = 1·75, L25 will be 0·883 925 237 509, and α = − 6231, 6 = +3854, whence the corrections are, −3850, +2381, and −1473, respectively, each giving 883 925 236 036.
page 265 note † T. Simpson's Mathematical Dissertations (1743), pp. 109 f. This rule gives a very close approximation. Conf. Hymers' Int. Calc., p. 181; Hutton's Mensuration, p. 374.
page 266 note * Conf. De Morgan's Diff, and Integ. Calc., pp. 262, 313–318; Woolhouse, Assurance Mag., vol. xi (1864), p. 309. By this method the computation might have been abridged in eome portions, had I noticed its advantages earlier.
page 266 note † MrWoolhouse, W. T. B., in a paper “On Interpolation, Summation, and the Adjustment of Numerical Tables,” in The Assurance Magazine, 1863–65 (vol. xi, pp. 61–88, 301–332, and vol. xii, pp. 136–176)Google Scholar, has developed a formula with necessary tables for interpolating terms in the middle interval of a series. The treatment ia interesting, and the formulæ are rapidly convergent, but not altogether convenient for computing a lengthy table.
page 267 note * Conf., e.g., De Morgan's Diff. and Integ. Calc., pp. 544, 545; and Woolhouse in Assur. Mag., vol. xi, p. 73, note.
page 267 note † Herschel, Examp. of Calculus of Finite Differences, p. 9. His table extends to Δ10010 (conf. De Morgan, Diff. and Int. Calc., p. 253.) This table is readily computed by the formula—
Δn+10m+1 = (n+1)(Δn0m + Δn+1 + Δn+10m).
That is, the sum of the quantities in the two lines for Δn and Δn+1, in the preceding column for 0m, multiplied by the index of Δ in the second line, gives the value in the 0m+1 column. thus Δ307 = 1806 + 8400 = 10206 and 10206 × 4 = 40824 = Δ408. The formula is derived from that for Δn0m, in Herschll's Appendix to Lacroix's Differ, and Integ. Calculus, (1816), p. 478.
page 270 note * This is only an altered mode of writing the formula given in De Morgan's Diff. and Integ. Calculus, p. 546; conf. Woolhouse, Assur. Mag., vol. xi, (1863), p. 68.
page 272 note * Analyse des Refractions astronomiques et terrestres (Strasbourg, 1799), p. 135.Google Scholar
page 272 note † Philos. Mag., xlii, (1871), p. 434. Conf. De Morgan, ut cit., § 117. Mr Glaisher remarks (p. 432) that “Kramp does not state what value he started from in applying the differences, or what means of verification he adopted. In all cases where a table is constructed by means of differences, the last value should be calculated independently, and then the agreement of the two values would verify all the preceding portion of the table.” And he adds that Kramp's value for t = 3 is in error in the tenth and eleventh figures, so that probably a portion of his table is incorrect in the last two figures (see § 4 above).
page 274 note * If we make t=0 in this series, r then becomes t, and we have the series in (9) from which it is derived.
page 277 note * It seems strange that the late Astronomer Royal, so late as 1861, should have adopted a value differing from that so generally recognised as correct at least to six decimal figures; he gives its reciprocal also as 2·096 665 (Theory of Errors, pp. 23, 24). Laplace (Théorie Anal, des Probabilités, 2e ed., p. 238), in one of the very few examples he gives, makes t2 = ·210 2497, which would give ρ = ·45853. M. Poisson, also (Connaissance des Temps, 1832, Add. p. 20), gives ·47414 for the value of ρ, and ·67336 for that of ρ???π, and again (Rech. sur la Prob. des Jugements, p. 208), he has ··4765 and ·6739 for the same quantities. Gauss (Werke, Bd. iv, S. 110) gave the value as ·476 9363, which is correct to the nearest figure in the seventh place. Lastly, O. Byrne (Dual Arithmetic, p. 200) finds 0·476 936 2744, which errs only in the last two decimal figures.
page 278 note * These constants will be met with, among other places, in Bessel's Fundamenta Astron., p. 18; and Ueber d. Bahn des Olberschen Kometen, in Abh. d. Math. Kl. d. Königl Preuss. Akad., 1812–13, S. 142; De Morgan's Theory of Probab., §§ 68, 100, 116, 150,152, etc.; Encke, in Berl Ast. Jahrb., 1834, Ss. 270, 293, 298; Gauss, Werke, Bd. iv, S. 6; Airy, Theory of Errors, pp. 23, 24; Poisson, Reck sur la Probab. des Jugements, p. 176, etc.
page 280 note * Conf. Airy's Theory of Errors, p. 24; Galloway's Treat, on Probability, §§ 145–148, pp. 194–197; De Morgan's Essay, p. 139.
page 281 note * Gauss, Bestimm. d. Genauigkeit d. Beobacht., § 2; Werke, Bd. iv, S. 110.
page 281 note † Or, the difference formula (38), given above, § 20, may be used to find these values.
page 281 note ‡ Trans. Camb. Phil. Soc., vol. xiii, (1883), pp. 145–272.
page 281 note § If we compute in succession, as is naturally the easiest method, the terms of the expression—
the sum of the 1st, 3rd, 5th, 7th, etc., terms will give the value of ![]() , whilst the sum of the quotients of the 2nd, 4th, 6th, 8th, etc., terms, divided respectively by 1, 3, 5, 7, etc., will give the value of H.
, whilst the sum of the quotients of the 2nd, 4th, 6th, 8th, etc., terms, divided respectively by 1, 3, 5, 7, etc., will give the value of H.
page 282 note * The differences of these values have been omitted from want of room on the page. The differences given throughout the tables are stated to the nearest figure in the last place, being taken from the computations.
page 282 note † Mr J. W. L. Glaisher's table (referred to above, § 4) of the values of G from t = 3·00 to 4·50 (Phil. Mag., 4th ser., 1871, vol. xlii. p. 436) is computed for differences of 0·01 and to seven significant figures, that is from eleven to fourteen decimal places; the appended table gives the values computed to fifteen places. But the values of L would enable us to carry them to a much larger number of figures.