No CrossRef data available.
Article contents
XXXI.—On the Partition of a Parallelepiped into Tetrahedra, the Corners of which Coincide with Corners of the Parallelepiped*
Published online by Cambridge University Press: 06 July 2012
Extract
It will be convenient first to fix a form of notation for the corners of the cube. With the origin within the cube and rectangular co-ordinates parallel to three edges meeting in a corner, the eight corners lie each in one of the eight octants, and may conveniently and symmetrically be represented thus:—
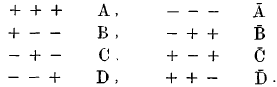
Or, calling any corner A, the corners distant √2 from A (the length of the edge being 1) and taken positively, i.e., contrary to the watch-hand way, as seen from A, are B, C, D (see figures).
So that, passing from corner to corner along an edge, we change both letter and sign, along a face diagonal we change letter but not sign, along a body diagonal we change sign but not letter.
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 37 , Issue 4 , 1895 , pp. 711 - 719
- Copyright
- Copyright © Royal Society of Edinburgh 1895
References
page 712 note * The letters Δ, I, L, and T have been chosen because they contain 3, 1, 2 and 2 straight lines respectively, as the corresponding tetrahedra contain 3, 1, 2 and 2 half-faces of the cube respectively. O, which contains no straight line, might have been chosen for the regular tetrahedron, as it contains no part of the surface of the cube, but, as 0 has been sometimes used to symbolise the regular octahedron, Ω a was selected, perhaps partly because this tetrahedron has twice the volume of any of the others.
page 713 note * If we leave out the condition forbidding new corners, we can obtain, from, this quinquepartite division, a case of division into six equal-volume tetrahedra, by cutting Ω into two equal tetrahedra by a plane containing one edge and bisecting the opposite edge.