Published online by Cambridge University Press: 06 July 2012
It is readily seen that the two differential equations

which play an important rôle in Professor Chrystal's mathematical theory of the Seiches, are special cases of the more general type
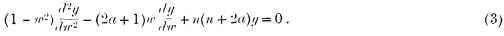
With regard to the first, the Seiche-equation, this becomes at once apparent by writing a= − ½. Equation (2), on the other hand, which we may briefly call the Stokes equation [see Professor Chrystal's paper on “Some further Results in the Mathematical Theory of Seiches,” Proc. Roy. Soc. Edin., vol. xxv.] will be recognised as a special case (a = + 1) of the equation
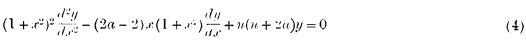
which is transformed into (3) by the substitution 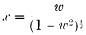 .
.
page 667 note * In § 45 of his Hydrodynamical Theory, Professor Chrystal investigates the case of a rectilinear lake, the floor of which would be represented in the above diagram by the straight line A B. The directions of the nodal loci E B in this figure suggest that the nodes in rectilinear lakes should be more displaced towards the shallow water than in any of the cases here considered, and this conclusion is indeed supported by the numerical results given in § 49 of Professor Chrystal's paper.—(Note added on June 30.)