No CrossRef data available.
Published online by Cambridge University Press: 06 July 2012
The purpose of the present paper is to ascertain how far it is possible to find exact solutions or values of x, y, &c., in equations between variables, so that the forms of plane curves and contour-lines of surfaces may be exactly determined. No approximate methods have been admitted, and only those methods have been used which are applicable to algebraic equations of every degree and any number of variables. In the examples given I have generally selected equations of even degree and even powers of the variables. But every such solution evidently includes the solution of the non-central equation of half the degree having corresponding terms and equal coefficients. The methods of solution employed are founded on the following introductory theorem or principle, which may be described as that of Homogeneous or Linear Variation of the quantities.
page 1075 note * For No. 8, the following additional values are necessary to trace the second inflexion—
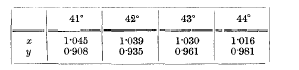
page 1075 note † For No. 9 we find also, θ = 44° 59'; x = 4·165; y = 4·163. And for other curves additional places have been computed where necessary for tracing the inflexions.
page 1076 note * The identity of the polar equations in the annexed tables with the Cartesian equations is proved as follows:—

Again, observing that—

page 1077 note * These values of log r are identical with those of No. 10 of the preceding table. In No. 15 the curve is referred to asymptotes.
page 1085 note * The numerical equation is
page 1093 note * These coordinates are very nearly the same as those of the ellipse described on the same axes.