Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T10:41:38.823Z Has data issue: false hasContentIssue false
  • English
  • Français

XV.—Expansion of Functions in terms of Linear, Cylindric, Spherical, and Allied Functions

Published online by Cambridge University Press:  06 July 2012

P. Alexander
Get access Rights & Permissions [Opens in a new window]

Extract

The expansion of ϕ(x) in terms of Go(x), G1(x), G2(x), &c., connected by a given law. being of great importance in mathematico-physical investigation, every method of effecting this expansion must have some interest for scientists.

I therefore proceed to propose what I think to be a new method, in the hope that it may prove to be useful.

Many special expansions of this nature have been effected by Fourier, Legendre, and others.

Type
Research Article
Information
Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 33 , Issue 2 , April 1888 , pp. 313 - 320
Copyright
Copyright © Royal Society of Edinburgh 1888

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 316 note * In the proof of (11) it has been assumed that gm is less than gn. The same may be proved for gm greater than gn by expanding (δ + gn)−1 in the reverse order.

page 319 note * Since writing this I have proved that if

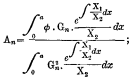
but I find that Sturm and Liouville have anticipated me (Liouville's, Journal de Mathématiques, vol. i., 1836)Google Scholar.