^{page 313 note *} It does not seem to have been noted before that

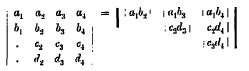
and that therefore

similarly, that

and therefore that

and generally that a determinant of order 2m is expressible as a sum of m! Pfaffians. When the Pfaffians are expanded the terms obtained are those given by Laplace's expansion-theorem.

^{page 313 note †} Philos. Magazine (1884), xviii. pp. 416–427;Google Scholar (1902) (6), iii. pp. 411–416.

^{page 314 note *} Sitzungsb. d. k. Akad. d. Wiss. (Berlin) (1882), pp. 821–824.

^{page 314 note †} Proccedings Roy. Soc. Edinburgh (1900), xxiii. pp. 142–154Google Scholar.

^{page 316 note *} To prove that

it suffices to show that the ten three-line determinants on the right are all represented on the left, and that nothing else than such representative are there to he found. Taking, for example, the fourth three-line determinant, , we partition it into , the first of which appears on the left in , the record in , and the third in . The number of such parts on the left being 5x4, and on the right 10 x 3, the other requisite is provided for.

^{page 317 note *} It would, of course, also vanish if each element in any one of its frame-lines were to vanish: that is to say, if equivalence of conjugates were confined to any one row of the determinant |a ₁b ₂c ₃d ₄e ₅f ₆|,—for example, if

a ₂,a ₃,a ₄,a ₅,a ₆ = b ₁,c ₁,d ₁,e ₁,f ₁.

This suggests a new avenue of investigation, and an avenue of special interest, because the number of conditional equations reqnisite for the evanescence of the aggregate may as here be less. Like previous writers, however, we are confining ourselves to vanishing produced by axisymmetry of a whole determinant.

^{page 318 note *} Observe that the result deducible regarding the evanescence of from making use of the fact that

is less extensive than that before obtained. In this connection it is well also to note that if three selected four-line coaxial minors of |a ₁b ₂c ₃d ₄e ₅f ₆| be axisymmetric, all the twelve others must be axisymmetric: for example, the axisymmetry of |a ₁b ₂c ₃d ₄, |a ₁b ₂e ₅f ₆|, |c ₃d ₄e ₅f ₆| implies the axisymmetry of |a ₁b ₂c ₃d ₄e ₅f ₆|.

^{page 318 note †} See Proceedings Roy. Soc. Edinburgh, xxiii., p. 147, § 5.