No CrossRef data available.
Article contents
VII.—The Automorphic Linear Transformation of a Quadric
Published online by Cambridge University Press: 06 July 2012
Extract
(1) It is well known that Cayley effected the transformation of
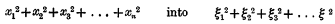
by introducing an intermediary set of variables
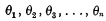
connected with each of the other sets by means of a linear substitution of a peculiar type. The substitutions in fact were
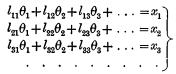
and
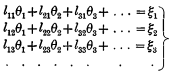
where the determinant of the first substitution is unit-axial and skew, and the determinant of the second substitution is got from the preceding determinant by changing rows into columns, and where, therefore, the number of arbitrary quantities introduced by the two substitutions is only ½n(n−1).
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 39 , Issue 1 , 1900 , pp. 209 - 230
- Copyright
- Copyright © Royal Society of Edinburgh 1900
References
page 209 note * Cayley, A., “Sur quelques propriétés des déterminants gauches,” Crelle's Journ., xxxii. pp. 119–123; or Collected Math. Papers, i. pp. 332–336.
page 210 note * Hermite, Ch., “Sur la théorie des formes quadratiques ternaires indéfinies,” Crelle's Journ., xlvii. pp. 307–312. See also xlvii. pp. 313–342; and Camb. and Dub. Math. Journ., ix. pp. 63–67.
page 210 note † Veltmann, W., “Die orthogonale Substitution,” Zeitschr. für Math. u. Phys., xvi. pp. 523–525.Google Scholar
page 212 note * Crelle's Journ., 1. pp. 288–299; or Collected Math. Papers, ii. pp. 192–201.
page 213 note * With the aid of this calculus, however, the proof is very simple, and will be seen to hinge entirely on the fact that Δ + Δ′=2D. At its fullest extent it stands as follows:—

Here Δ′ is the matrix got from Δ by changing rows into columns: but this relationship is not a necessity for the existence of the identity, which will hold if Δ, D, Δ′ be any three matrices whatever fulfilling the condition Δ+Δ′=2D.
page 214 note * Trans. Roy. Soc. Edin., xxxii. pp. 461–482.
page 217 note * Since this was written I have ascertained that the simplification here given of Cayley's solution was known to Frobenius, whose paper of the year 1877, “Ueber lineare Substitutionen und bilineare Formen” (Crelle's Journ. lxxxiv. pp. 1–63) is a carefully written and methodically arranged exposition of the theory of matrices with applications. It would appear not to have received due attention from subsequent writers.
The simplification is also explicitly referred to in one of a series of valuable papers by Dr Henry Taber in the Proc. Lond. Math. Soc. (1890–93).
page 217 note † Crelle's Journ., xxxii. pp. 119–123; or Collected Math. Papers, i. pp. 332–336.
page 220 note * See also the third line of the proof that D−1 Δ′Δ−1 = Δ−1Δ′ in the footnote to § 6.
page 226 note * Muir's Theory of Determinants, p. 213, § 179; or Trans. Roy. Soc. Edin., xxx. p. 2.


