No CrossRef data available.
Article contents
IX.—Some Identities connected with Alternants, and with Elliptic Functions
Published online by Cambridge University Press: 06 July 2012
Extract
(l) Cayley in his paper entitled “Note sur l'addition des fonctions elliptiques” obtains among other similar things an expression for
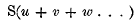
in terms of
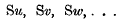
where

The form of the expression is the quotient of two determinants, and as the expression becomes useless for such cases as u = v, u = w, … on account of the simultaneous vanishing of numerator and denominator, he is led to seek a means of throwing out the common evanescent factors.
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 40 , Issue 1 , 1905 , pp. 187 - 201
- Copyright
- Copyright © Royal Society of Edinburgh 1905
References
page 187 note * Crelle's Journ., xli. pp. 57–65; or Collected Math. Papers, i. pp. 540–549.
page 188 note * These cofactors are incorrectly printed both in the original journal and in the collection, and unfortunately the mistake consists in putting small letters in place of capitals.
page 189 note * Another theorem on the same subject may be illustrated by the same example, viz.:

Here only one row or column of the original determinant is multiplied, the multipliers being complete terms of the symmetric function. Each multiplying term, it will be observed, is used three times, and occurs in a different position every time; for example, the cofactor of A2B on the right is

which is equal to |a 1b 1c 1| as it should be.
page 200 note * A direct proof that
is obtainable from the theorem above given regarding the sum of two fourth-order determinants, the parents being the two determinants on the right, and the progeny the six determinants obtainable on the left by performing the multiplications indicated, viz.:



