1 Introduction
Models are of fundamental importance in contemporary product development. For instance, drawings, physical or CAD models are used to generate designs, and finite element analysis or computational fluid dynamics models can help evaluate these. Other models aim to tackle the considerable complexity and interconnectedness exhibited by design projects, capturing the underlying structure of development processes or resulting products to offer support for design and planning decisions. Such models, and simulations based on them, are in the focus of this article. In many contexts engineers and managers interact closely with models and base many decisions on them. Understanding the model properties that might influence such decisions is therefore crucial. This research focuses on a key attribute of models – their granularity – and offers a multidisciplinary theoretical perspective as well as a classification framework, outlining the main dimensions of model granularity. The aim of this article is to contribute to the understanding of the nature of model granularity, to illustrate how this may relate to models in engineering design and thus to provide a resource for modellers navigating decisions regarding granularity.
1.1 Model granularity in engineering design
Models are abstract representations of their target system, the part of reality they choose to capture, created for a specific purpose (Frigg Reference Frigg2003). Depending on how and to what extent the description of the target system is abstracted, the emerging model comprises a certain level of granularity. We use the term granularity to describe, broadly speaking, the level of detail in the description of the target system. What makes models in engineering design particularly interesting is that they are used for analysis (like models in science) but also for synthesis. Modelling for synthesis goes beyond merely describing the target system as it is – it also prescribes or proposes how it should be, which poses a different set of challenges. The target system does not yet physically (or even conceptually) exist when the modelling is undertaken. So, the choice of model granularity has implications beyond the performance of the model itself and impacts the target system. For instance, product model granularity can influence modularisation of system architectures (Chiriac et al. Reference Chiriac, Hölttä-Otto, Lysy and Suh2011) or sequencing of integration tasks (Eppinger et al. Reference Eppinger, Joglekar, Olechowski and Teo2014). Process models have to account for the fact that product development processes are multidisciplinary, interdependent, parallel and iterative (Browning, Fricke & Negele Reference Browning, Fricke and Negele2006) and can exhibit considerable uncertainty (Wynn, Grebici & Clarkson Reference Wynn, Grebici and Clarkson2011). In engineering design there is a distinction between product and process modelling, which are often handled separately but can also be integrated (see e.g., Eckert et al. Reference Eckert, Albers, Bursac, Chen, Clarkson, Gericke, Gladysz, Maier, Rachenkova, Shapiro and Wynn2015). In either case, granularity choices in one domain can influence the other and models within one domain each other. For example, the granularity of a product model can influence design process simulation and task sequencing (Maier et al. Reference Maier, Wynn, Biedermann, Lindemann and Clarkson2014; Maier, Eckert & Clarkson Reference Maier, Eckert and Clarkson2015). Despite the apparent importance of model granularity in the field of engineering design, relatively few research contributions address the topic directly. Indeed, it is often assumed that some appropriate level will be determined without considering the sensitivity of the results (Chiriac et al. Reference Chiriac, Hölttä-Otto, Lysy and Suh2011).
Notwithstanding the special features of modelling and simulation in engineering design, the discussion of granularity is also relevant to other fields. Extending the search to other relevant modelling domains thus yields some more approaches to the topic. However, these discussions often remain on a very theoretical level, making them less accessible for engineers and designers, who often have limited modelling expertise (Wynn Reference Wynn2007; Eckert & Clarkson Reference Eckert and Clarkson2010). More recent studies have demonstrated the impact model granularity can have on analysis (e.g., Chiriac et al. Reference Chiriac, Hölttä-Otto, Lysy and Suh2011; AlGeddawy & ElMaraghy Reference AlGeddawy and ElMaraghy2015; Samy, AlGeddawy & ElMaraghy Reference Samy, AlGeddawy and ElMaraghy2015; Suh, Chiriac & Hölttä-Otto Reference Suh, Chiriac and Hölttä-Otto2015). This highlights the importance of the topic not only from a practical point of view but also emphasises the need for accessible support that captures and synthesises the various perspectives of model granularity and shows their pertinence for engineering design.
1.2 Significance for modelling practice
Model granularity has implications for modelling practice from design and analysis through to reuse phases. Determining an appropriate granularity level for a particular purpose is a modelling choice that may have to be traded off with a number of other considerations. The scope or boundaries have to be defined, a modelling approach has to be chosen and individual choices have to be made regarding how to represent particular real-world entities (Eckert & Stacey Reference Eckert, Stacey, Heisig, Clarkson and Vajna2010). For instance, two tightly coupled tasks may be modelled as one, simplifying the model but concealing iterative behaviour, or as two separate tasks, capturing the iteration loop. Such choices depend on the model user and the decision that should be supported (e.g., Browning et al. Reference Browning, Fricke and Negele2006), which induces a set of more or less clearly articulated requirements. An example is the development of models for managers, which Little (Reference Little1970) recommends to be simple, robust, easy to control, adaptive, complete on important issues and easy to communicate with. The intended purposes driving such considerations and modelling choices, such as granularity, are manifold and often specific to particular contexts (Browning Reference Browning2009), which in turn limits reproducibility (Kasperek et al. Reference Kasperek, Maisenbacher, Kohn, Lindemann and Maurer2015). In a review of activity network-based process models, Browning & Ramasesh (Reference Browning and Ramasesh2007) distinguish four categories of purposes: project visualisation, planning, execution and control, and development. Building up on this, Browning (Reference Browning2010) provides an overview of 28 potential purposes of process models, identified in a series of interviews. For example, the purposes ‘estimate project time, cost, quality, and risks’ or ‘allocate resources’ may require rather more fine-grained models and data than the purpose ‘visualise, understand, analyse, and improve processes’, which requires information to be presented in an accessible way.
In many cases choosing a level of granularity involves balancing cost-benefit considerations. The effort to build and analyse models often depends on their granularity. For instance, achieving consensus around abstract models can be time consuming in a different way than constructing a highly detailed model. Depending on the chosen level of granularity, particular skillsets and computational resources may be required to develop and analyse a model, impacting on resource requirements. The effort to manage, deploy and maintain detailed models can be relatively high. Also, depending on the scenario, eliciting the information required by fine-grained models can be challenging, as in many cases the necessary information is not readily available.
Given the associated cost, in most cases there are a number of good reasons for choosing a particular level of granularity. If a certain minimum level of detail is strictly required, then the only question is if adding more serves the purpose. In most cases, identifying this minimum level should be the aim (Robinson Reference Robinson2007). In practice, however, determining this point is usually not straightforward and factors other than model accuracy or fidelity have to be factored in to decisions regarding model granularity. For instance, if a number of models of a particular target system exist it can be important to keep them congruous across different levels of granularity to avoid inconsistencies. Also, adding more detail to a model does not necessarily result in higher fidelity. It can, instead, also decrease the value of model, making it too complex, harder to calibrate, use and interpret (e.g., Pidd Reference Pidd1999).
1.3 Article structure
This article sets out to briefly describe the underlying research methodology in Section 2. A theoretical perspective on models and modelling is offered in Section 3. Definitions of model granularity and related concepts are reviewed and discussed more generally in Section 4, before focusing on the implications for engineering design. Based on that, Section 5 categorises the different manifestations of model granularity and illustrates the resulting framework by applying it to a dependency structure model. The challenges and opportunities related to model granularity are explored in Section 6, before the presented framework and the limitations of the research are discussed in Section 7. Finally, Section 8 reviews the contribution, draws conclusions and briefly explores areas for further work.
2 Research approach
This research was prompted by the authors’ empirical insights from an array of modelling projects in the service and design domains. Over a period of
$2{\textstyle \frac{1}{2}}$
years, various models of different kinds were developed in close collaboration with industry, ranging from large scale product structure models to fairly complex service process simulations. This also involved eleven semi-structured interviews and an online questionnaire capturing practitioners’ perspectives on their modelling processes. Each of the developed models presented challenges related to its granularity in some form. Even though these issues were rather fundamental to achieving satisfying outcomes, surprisingly little research or practical guidance was identified in a review of the engineering design literature. Also, due to the abstract nature of the topic and the lack of theoretical background it was at times difficult to even discuss the arising issues in a meaningful and constructive manner.
Motivated by the perceived lack of research in the field of engineering design, the literature review was extended to a wide field of domains, including philosophy of science, artificial intelligence, network theory, complexity science, information theory and the wider modelling and simulation literature. In this process it became apparent that the use of terminology to describe model granularity and related concepts differs across and within disciplines. The lack of an appropriate organising framework prompted the creation of a list of terms describing aspects of model granularity, supplemented with quotes and continuously refined in an iterative process among the authors, with input from expert modellers in industry. The objective was to collate widely used terms describing model granularity, activities determining it and model properties resulting from it, with a focus on their relevance for engineering design. This yielded an overview of the use of terminology, supplemented by relevant definitions, illustrating perspectives on (model) granularity across research communities. Because no prior work attempting to provide such an overview was identified, the selection is a result of studying the use of terminology in literature and modelling practice. Analysing and synthesising the theoretical approaches towards the topic across domains helped define the notion of granularity, delimit it from related terms and overall conceptualise the classification framework presented in this article. The literature research also included analysis of more practical approaches towards handling challenges associated with model granularity, which revealed additional insights regarding motivation, techniques and issues encountered in practice.
To address the lack of relevant discussion and the resulting difficulties in conceptualising and describing model granularity, literature was used to derive a classification framework to assist model builders. This framework aims to categorise the different manifestations of model granularity and thus promote understanding and organisation of the topic. As a theoretical contribution motivated by and relevant to practice, the results should be accessible not only to researchers interested in model theory but also to modelling practitioners. This conceptual framework makes assumptions explicit and opens them up for discussion. The classification framework is illustrated with Design Structure Matrices, a common modelling approach in engineering design, to provide a more practical reference point in an otherwise predominantly theoretical debate. In the process of developing the framework, it was continually refined and discussed with other researchers and practitioners.
3 A theoretical perspective of models and modelling
Given that granularity is a model attribute that is impacted not only by the modelling process but also shapes model appearance and behaviour, it is important not to discuss it in isolation. So, before model granularity is discussed specifically, this section provides some theoretical background on modelling more generally and the role of abstraction in this process. Even though modelling and simulation has emerged as a big field of research in several domains over the last decades, there is comparably little work contributing to a theoretical understanding of the nature of models and modelling. While such a theoretical approach is not necessary to build models it can help discuss and understand the implications of how we build (and use) models.
A number of theoretical contributions about models and modelling can be found in the Philosophy of Science community. Focus within this domain is largely on models used in the sciences, which aim to represent real-world phenomena rather than representing or generating artificial systems like models in engineering and design (Boon & Knuuttila Reference Boon, Knuuttila and Meijers2009). However, the concepts and vocabulary of this more mature discussion can be useful to discuss models in general.
3.1 The relationship between model and target system
Discussions of models in philosophy of science often focus on the theme of representation. The structuralist view of modelling has been an influential perspective, where models are seen as structures (entities and their relations) which represent their target system (Frigg Reference Frigg2003). Simply speaking, proponents of this view regard models as isomorphic representations of the structure of their target system (see e.g., Suppe Reference Suppe1977). However, in more recent discussions, there has been a shift away from this structuralist view and its limitation to a dyadic relationship between model and target system towards a triadic relation that involves either users or interpretation (Knuuttila Reference Knuuttila2005). While isomorphism has the advantage of enabling precise formalisation, it falls short when the real-world system is not a structure in an obvious way. Isomorphism also implies a symmetric relation between model and target system, which does not fit actual modelling practice in science, where models are meant to be representations of their target system, and not vice versa. Including the modeller’s intention, or the purpose, establishes directionality in the relationship between representation and target system.
Other, more pragmatic attempts at describing representation take account of the limitations of isomorphism and claim, for example, that representation is based on some form of similarity (Giere Reference Giere2004). However, this can still be seen as limiting due to the focus on representation, which is only one of the conceivable uses of models (Knuuttila Reference Knuuttila2005). Morrison & Morgan (Reference Morrison, Morgan, Morrison and Morgan1999) adopt a wider perspective by describing models as mediators, “autonomous agents …[who] function as instruments of investigation” (p. 10). According to them, it “is precisely because models are partially independent of both theories and the world that they have this autonomous component and so can be used as instruments of exploration in both domains” (p. 10). They emphasise the various ways models can support problem solving and thus hint at their epistemic value in, but also beyond, representing their target system. Knuuttila (Reference Knuuttila2005) extends this perspective by describing models as epistemic artefacts, which provide us with knowledge in many other ways than just abstract representation. Such representation does not only consist of the model as an artefact in itself but also includes an intentional relation of representation, connecting the artefact with the target system. This implies that the model can be detached from this relation and therefore allow for different interpretations and thus different representations.
The relationship between target system and models used in engineering, and in particular engineering design, can differ from the sciences. While scientific models usually aim to represent some real target system, often with the goal of isomorphism or similarity, engineers can be thought of as actively intervening with the world. “Instead of depicting an already existing world, the engineering sciences aim at theories and models that provide understanding of artificially created phenomena” (Boon & Knuuttila Reference Boon, Knuuttila and Meijers2009, p. 688). This is an important observation and, despite targeting the engineering sciences rather than design, equally hints at some of the challenges encountered when describing the relationship between model and target system in engineering design. Boon & Knuuttila (Reference Boon, Knuuttila and Meijers2009) advocate a pragmatic account of models as epistemic tools rather than representations of a real target system. While they focus on models in engineering science, aiming at scientific understanding of system behaviour or material properties, it is argued here that the same applies to engineering design. When modelling for design, assumptions and choices have to be made regarding how to present an artificial system according to a particular purpose. So, models in engineering design share some properties with scientific models but they are also less straightforward in certain respects; their target system is often less clearly defined, highlighting the significance of purpose, scope and choices regarding model granularity.
3.2 Modelling as abstraction from reality
Before focusing on the role of abstraction in modelling, it is worth recapitulating what the term modelling describes in the scope of this research. With reference to Turnitsa (Reference Turnitsa2012), who distilled the following definition of modelling from various sources in the modelling and simulation literature, Tolk & Turnitsa (Reference Tolk and Turnitsa2012) state: “Modelling is the purposeful process of abstracting and theorizing about a system, and capturing the resulting concepts and relations in a conceptual model” (p. 2). The emphasis on conceptual models results from their focus on computational models, which might not be appropriate in all contexts. For instance, sketches, drawings, and physical prototypes are all models used in engineering design but are beyond the scope of this article. Still, there are a number of insights that can be drawn from this definition. First, it highlights that purpose is central to modelling activities. Second, it states that modelling is a matter of abstracting and is based on theory. Third, the goal is to capture both concepts and relations, or dependencies, in the emerging model.
The importance of abstraction for modelling and simulation is discussed in a variety of fields, ranging from discrete-event simulation (Zeigler, Praehofer & Kim Reference Zeigler, Praehofer and Kim2000) to artificial intelligence (Saitta & Zucker Reference Saitta and Zucker2013). In many accounts abstraction is seen as the crucial step in representing the real-world target system in a (conceptual) model (e.g., Frantz Reference Frantz1995). This process results in a particular level of abstraction of the developed model, which is usually reached from either a bottom-up direction or a top-down direction. Bottom-up generally consists of aggregating elements of the target system, leading to a more abstract description. For instance, a number of specific tasks could be aggregated to describe the overall activity. Conceptually, the term ‘aggregation’ can be thought of as a subset of ‘abstraction’ (Fishwick Reference Fishwick1988). On the other hand, top-down approaches involve decomposition of a more abstract description into smaller, more concrete parts. For instance, the description of a car could be decomposed into descriptions of engine, transmission, body etc.; and a description of an engine into descriptions of crankshaft, pistons, cylinder heads etc. Depending on the context, the purpose and the data available both bottom-up and top-down approaches can be employed in modelling.
So, different levels of abstraction can be obtained in a model depending on how, or to what degree, the target system is abstracted. Floridi (Reference Floridi2008) notes that while a level of abstraction formalises the scope or granularity of a model, a gradient of abstraction presents a way of varying the level of abstraction so observations can be made at differing levels. Different levels of abstraction usually imply an underlying hierarchical structure, which relates different levels with each other. The value of multilevel abstraction has been discussed in disciplines like complex systems design (Alfaris et al. Reference Alfaris, Siddiqi, Rizk, de Weck and Svetinovic2010) and business process modelling (Eshuis & Grefen Reference Eshuis and Grefen2008). The overall motivation is the ability to provide consistent models on different levels, depending on purpose and stakeholders. This also highlights some of the challenges associated with abstraction in general and multilevel models in particular. There is an epistemological issue regarding how multiple levels of abstraction are derived. Both aggregation and decomposition are employed in modelling products and processes, but it depends on factors like data availability, knowledge and the type of target system to determine an appropriate approach. Also, there is a range of practical issues, like ensuring and maintaining consistency across abstraction levels (Smirnov et al. Reference Smirnov, Reijers, Weske and Nugteren2012), choosing appropriate levels (Eshuis & Grefen Reference Eshuis and Grefen2008) and abstraction techniques (Frantz Reference Frantz1995) as well as the impact the different levels can have on analysis (Chiriac et al. Reference Chiriac, Hölttä-Otto, Lysy and Suh2011).
4 Granularity in modelling and simulation
Finding a suitable level of granularity in a model is critical to ensure that the model is as detailed as necessary, but does not unduly confuse the user or distort the results. Therefore, it is useful to understand what granularity entails and how it can be assessed. One of the challenges when discussing granularity is the lack of understanding and clear terminology. Research targeting model granularity in engineering design is limited, but other communities have approached the topic, sometimes using different vocabulary. This section provides an overview of conceptualisations of relevant terms and how they relate to model granularity. It also introduces different measures of granularity as they offer a different perspective on granularity and may provide guidance in assessing granularity levels across larger and multilevel models.
Table 1. Definitions of terms describing granularity or corresponding concepts.
4.1 Model granularity and related concepts
In addition to a smaller number of explicit approaches towards the topic of model granularity, a range of related issues are discussed in the literature. In particular, discussions around model abstraction, decomposition, levelling, complexity, clustering and hierarchies are useful when approaching the topic of model granularity. The most relevant concepts are briefly presented here (see also: Maier, Eckert & Clarkson Reference Maier, Eckert and Clarkson2016) and grouped in three categories:
-
∙ Concepts describing model granularity or similar notions (Table 1).
-
∙ Concepts describing activities that impact model granularity (Table 2).
-
∙ Concepts describing model properties that may result from their granularity (Table 3).
Some of the concepts could be attributed to multiple categories, which is illustrated in Figure 1 and briefly discussed at the end of this section. Apart from ‘granularity’ the terms are ordered alphabetically and the order of definitions does not imply a ranking of their relevance.
Granularity refers to a property of the model itself and is characterised more or less formally, depending on the discipline. Mathematical definitions are based on set theory and consider cardinality, size and interaction of subsets (Yao & Zhao Reference Yao and Zhao2012). In engineering design, the size and detail of model elements determine its granularity, which is commonly understood to result from (hierarchical) decomposition (Chiriac et al. Reference Chiriac, Hölttä-Otto, Lysy and Suh2011; AlGeddawy & ElMaraghy Reference AlGeddawy and ElMaraghy2013). We refer to the granularity of a model as a manifestation of the level of detail in which it represents its target system. In particular, granularity may be used to describe the size and information content of model elements as well as the nature of relationships between model elements. Granularity can also relate to the resolution of output obtained through analysis based on a model.
Even though abstraction is frequently mentioned with regards to modelling and simulation, formal definitions are harder to find. The term abstraction is mostly used in a more conceptual manner (Cartwright Reference Cartwright1999) when describing modelling activities or resulting levels of abstraction (e.g., Fishwick Reference Fishwick1988). Abstraction is a fundamental part of most modelling endeavours (Frigg Reference Frigg2003), leads to a particular level of abstraction of a model and thereby drives its granularity. So, abstraction in the modelling process determines model granularity.
Complexity is a topic that is extensively discussed in various fields and even emerged as a research field on its own: complexity science (Ladyman, Lambert & Wiesner Reference Ladyman, Lambert and Wiesner2013). Without going into further detail, a complex system can be said to consist of multiple components interacting in non-simple ways (Simon Reference Simon1962). While the notion of complexity is generally used to describe real-world systems, it is also used for models (see definitions in Table 1). With respect to model granularity, this concept is therefore important in two respects. First, capturing a more complex system may require a more detailed, fine-grained model. Second, complexity can also refer to the model itself, describing either the number of elements and their connectedness or the difficulty to understand and work with them (Edmonds Reference Edmonds1999). In many cases a larger, more fine-grained model will also be considered more complex. Related, yet distinct, is the notion of complicatedness (or cognitive complexity), which refers to the observer-dependent, subjective dimension of complexity (e.g., Ramasesh & Browning Reference Ramasesh and Browning2014). While the term complicatedness is used to describe systems generally, it also has implications for models and can provide a proxy for understandability. A fine-granular, complex model may not be perceived as complicated by a user if it is architected and displayed in a simplified or abstracted way, thereby making it more easily understandable. Tang & Salminen (Reference Tang and Salminen2001) refer to this as ‘architected complexity’.
The organisation of complex systems is often characterised as multilevel hierarchies of systems and subsystems (Simon Reference Simon1962; Alexander Reference Alexander1964; Ladyman et al. Reference Ladyman, Lambert and Wiesner2013). This can be observed in many aspects of the natural world (organisms, ecosystem or the cosmos itself) but also in man-made systems. Hierarchical structures are important when reflecting on model granularity. Depending on the chosen approach, aggregation or decomposition both lead to hierarchical structures, which strongly influence the resulting model granularity. In addition to such part-whole relations, hierarchies can also result from specialisation and generalisation, indicating ‘is a’ relations (Brachman Reference Brachman1983). The resulting hierarchical structures are referred to as taxonomies and play an important role in fields such as requirements and software engineering. Interactions between parts of the system on different levels of the hierarchy contribute to complex behaviour. Models that offer different levels of granularity are often based on a hierarchical structure – of data or model architecture.
Model resolution is very closely linked with model granularity and is in many cases used to describe similar ideas. It is often associated with the amount of detail a model includes to represent its target system (Tolk Reference Tolk and Tolk2012). Some authors also use the term to describe the precision of a model’s output (Weld Reference Weld1992). Resolution is perhaps the closest related concept to granularity given that both are directly proportional – a high resolution requires a fine granulation, be it of pixels in an image or elements in a model.
Table 2. Definitions of terms describing activities that influence granularity.
Aggregation and decomposition are often used as opposite directions of constructing models, the latter also sometimes being referred to as disaggregation (Benjamin et al. Reference Benjamin, Erraguntla, Delen and Mayer1998). Aggregation refers to a bottom-up approach where elements of a model are grouped together and described on a higher level of abstraction (Iwasaki & Simon Reference Iwasaki and Simon1994). In many cases, this leads to a loss of information, although the goal of model aggregation generally is to conserve information from more detailed levels. Aggregation results in coarser grained models. Decomposition denotes a top-down approach where system elements are broken into a set of smaller elements or subsystems (Alfaris et al. Reference Alfaris, Siddiqi, Rizk, de Weck and Svetinovic2010). This usually adds information about the decomposed systems but also requires additional effort to elicit the required information. Similarly, granulation describes the decomposition of a universe into subsets (although Yao (Reference Yao2003) also uses it to indicate clustering of elements into groups, which is elsewhere distinguished as ‘organization’ (Zadeh Reference Zadeh1997)). We suggest using Zadeh’s (Reference Zadeh1997) original definition of the term granulation, referring to the decomposition of a set, to avoid confusion. Decomposition generally leads to more fine-grained models. For both concepts a range of drivers and approaches exist that are employed depending on the context and purpose of the model.
Clustering aims to group elements of a model that are strongly interconnected into clusters, while minimising the connectivity outside of the clusters (Browning Reference Browning2001). Clustering is a representative example of a type of analysis that forms subsets based on the relationships between model entities, which may also focus on the sequence of design tasks or the responsibility of (teams of) engineers. In engineering design such approaches are often used to modularise product structures, where tightly coupled components are grouped into modules, which are then more loosely coupled with the rest of the system (Chiriac et al. Reference Chiriac, Hölttä-Otto, Lysy and Suh2011). Models can also be clustered on multiple levels, which leads to hierarchical structures. Clustering can be used to aggregate a model, thereby transforming it to a coarser grained instance. Also, the size and number of clusters depend on the granularity of the original model and the desired granularity of the clustered model.
Table 3. Definitions of terms describing model properties that may result from its granularity.
Figure 1. Relationships between the notion of model granularity and related concepts.
Model accuracy can describe the degree to which the model constructs or its output conform to reality (Gross et al. Reference Gross1999). Similarly, precision can describe both a quality of the model itself as well as the results that are obtained from it (Gross et al. Reference Gross1999). A clear distinction between the terms can be made, as emphasised in literature on measurement systems analysis and Six Sigma. Here, ‘accuracy is the closeness of average measurements to reference values’ and ‘precision is the closeness of measurements to each other’ (Sleeper Reference Sleeper2005). According to this definition a model could be precise (consistent results with little variation) but not accurate (results do not conform to reality) and vice versa. It can be argued that both accuracy and precision often depend on the granularity of the model – certain aspects of reality can only be accurately or precisely described by going into a larger amount of detail. On the other hand, a fine-granular model is not automatically accurate/precise and an accurate/precise model does not necessarily have to be fine grained. The term validation typically describes an assessment of model accuracy with respect to its intended purpose (Sargent Reference Sargent2005).
The discussion of model granularity is closely related with the more specific notion of model fidelity, which is also sometimes described with reference to accuracy (Tolk Reference Tolk and Tolk2012, p. 17). In the context of modelling and simulation fidelity has been defined as the ‘degree to which a model or simulation reproduces the state and behaviour of a real world object’ in a report that provides a comprehensive account on model fidelity (Gross et al. Reference Gross1999, p. 3). While this definition hints at the impact model granularity has on fidelity, it is important to note that the two are not the same (even if they are sometimes used to describe similar phenomena). Fidelity describes the quality of a model to represent the real world and thus refers to the relationship between model and target system. On the other hand, granularity describes a property of the model itself, which may be influenced by the characteristics of the target system and impact the model’s fidelity. Weisberg (Reference Weisberg2007) distinguishes two types of fidelity criteria: dynamical and representational fidelity criteria. Dynamical fidelity criteria indicate how close the model output must be to its real-world counterpart. Representational fidelity criteria are more complex and specify, for instance, to what extent the model structure has to match the real-world phenomenon’s causal structure.
To provide an overview of relevant concepts and how they relate, Figure 1 depicts a relationship diagram, picking up the three categories defined in the beginning of this section. To keep it concise, the diagram focuses on how the concepts relate to granularity and only presents a selection of relationships without too much detail. Some of the terms could be placed at different points in the diagram. For example, the term abstraction can describe an activity that impacts model granularity but also a model property that is closely related to granularity. Likewise, resolution can refer to granularity of the model as well as the output. Also, the modularity of a model may depend on its granularity but the modularity of the target system can in turn influence model granularity. These terms are therefore drawn across categories.
4.2 Measuring granularity
Measures offer ways to quantify model granularity and related concepts to help modellers navigate challenges associated with large, hierarchical or multilevel models. Some metrics that aim to capture granularity have been suggested in various fields and a range of metrics exists for related concepts, such as complexity (e.g., Summers & Shah Reference Summers and Shah2010). Due to the number of relevant contributions and the challenges associated with quantifying granularity, this section only provides a brief introduction to the topic, including a number of references for further reading. The presented metrics are not intended as recommendations, which would require a focused study, but rather as representative examples. Granularity metrics and the underlying theories offer an important perspective on the characterisation of model granularity because they formalise concepts in an explicit way and allow for quantification. In a contribution to rough set theory, Yao (Reference Yao2003) proposes an information-theoretic granularity metric
$G$
based on the Shannon entropy to quantitatively characterise partitions:
$$\begin{eqnarray}\displaystyle G(\unicode[STIX]{x1D70B})=\mathop{\sum }_{i=1}^{m}\frac{|A_{i}|}{|U|}\log |A_{i}| & & \displaystyle\end{eqnarray}$$
$G(\unicode[STIX]{x1D70B})$
denotes the granularity of partition
$\unicode[STIX]{x1D70B}=\{A_{1},A_{2},\ldots ,A_{m}\}$
of a universe
$U$
, where
$|\cdot |$
denotes the cardinality of a set. The value of
$G(\unicode[STIX]{x1D70B})$
ranges from 0 (‘atomic’ granularity; as fine grained as the universe) to
$\log |U|$
(where the model only comprises one granule). Holschke, Rake & Levina (Reference Holschke, Rake, Levina and Dayal2009) adapt this metric to quantify the granularity of business process models, noting the need for a ‘baseline’ in order to compare different models (Holschke Reference Holschke, Hull, Mendling and Tai2010). Indeed, knowledge about the cardinality of the universe (or target system) is necessary to quantify the granularity of a partition (or model). Yao & Zhao (Reference Yao and Zhao2012) take a measurement-theoretic contribution in proposing a new class of measures for granularity of partitions. They distinguish between the granularity of a set, which depends on the cardinality of the set, and the granularity of a partition, which depends on the expected granularity of its blocks. Additionally, they include a critical review of existing information-theoretic and interaction based granularity measures. Dai & Tian (Reference Dai and Tian2013) define the concept of knowledge granulation and knowledge granularity measure for set-valued information systems. Further discussions of the term granularity and approaches to measuring it exist in fields such as information theory, cognitive informatics and granular computing but are not reviewed here.
In the engineering design domain, AlGeddawy (Reference AlGeddawy2014) proposes a ‘granularity index’ to quantify the quality of Design Structure Matrix (DSM) (e.g., Steward Reference Steward1981; Browning Reference Browning2001) clustering in the environment of product families. The collective, numeric DSMs used are combined from individual, binary product variant DSMs.
$$\begin{eqnarray}\displaystyle \text{Granularity Index }=P-Z-\mathop{\sum }_{i=1}^{m}(N_{i}-1)\cdot (A_{i_max}-A_{i_min}) & & \displaystyle\end{eqnarray}$$
$P$
is the sum of positive matrix elements inside DSM clusters and
$Z$
is the number of zero elements inside DSM clusters. The summation term is the component appearance variability for all clusters and equals the sum of component appearance variability across modules.
$N_{i}$
is the number of components in a specific module and
$A_{i_max}/A_{i_min}$
is the maximum/minimum number of appearances of any component in the module. This Granularity Index is calculated for each granularity level of a hierarchical clustering obtained through cladistics (AlGeddawy & ElMaraghy Reference AlGeddawy and ElMaraghy2013). The clustering with the highest Granularity Index is then recommended for product family module composition.
Apart from metrics explicitly targeting granularity, others can also be used to quantify certain aspects of model detail. For example, in their investigation of the impact of model granularity on modularity, Chiriac et al. (Reference Chiriac, Hölttä-Otto, Lysy and Suh2011) do not use an explicit metric of granularity. Instead they use three modularity metrics to quantify the effects of granularity changes, which are quantified in terms of the size and density of the DSM, focusing on the structural aspects of granularity. Complexity metrics have been used to quantify the complexity of design problems, products and processes (Ameri et al. Reference Ameri, Summers, Mocko and Porter2008). Building up this, Summers & Shah (Reference Summers and Shah2010) propose measuring three different aspects of complexity: size, coupling and solvability. Size complexity is based on entropic measures and thus comparable to granularity metrics (e.g., Yao & Zhao Reference Yao and Zhao2012). Integrating modularity and additional details about connectivity is suggested to better capture system complexity (Tamaskar, Neema & DeLaurentis Reference Tamaskar, Neema and DeLaurentis2014). Complexity metrics generally focus on design processes and products themselves rather than models thereof. They also include aspects that go beyond granularity, such as solvability of design problems or modularity of product architectures. Real-world complexity may drive but also provide a baseline for assessing model granularity.
Quantitative analysis of granularity provides the opportunity to quickly assess and compare models, which can ultimately contribute to making better modelling choices. However, measuring model granularity is a challenging endeavour. One question is whether absolute or relative measures are more appropriate. Most information-theoretic metrics define granularity relative to a baseline but still have an absolute scale (Yao & Zhao Reference Yao and Zhao2012). This seems to make sense but requires quantifying the target system itself, which may not be straightforward (Holschke Reference Holschke, Hull, Mendling and Tai2010). Relative measures can be useful to compare models of the same target system but make less sense for different target systems. Also, applying existing metrics without clarifying what exactly they represent may not lead to meaningful results (Fenton Reference Fenton1994). In order for a metric to be a useful measure of model granularity, it has to capture underlying empirical relations (Roberts Reference Roberts1985). However, this requires a theoretical foundation, clarifying which aspects of granularity are measured and how this relates to observable model properties. This research aims to provide such a foundation by developing a framework that classifies different dimensions of model granularity (Section 5), rather than to derive measures, which would merit a more comprehensive and focused discussion than is feasible in the scope of this article.
4.3 Approaches towards model granularity in engineering design
Despite the limited attention in the engineering design community, there are a number of approaches directly targeting model granularity, some of which are presented in this section. Other contributions deal with the topic more or less directly, including work on clustering, modularity, decomposition, hierarchy and others (see also Section 4.1). Most of this work focuses on the product domain although it can be argued that it is just as important for the process domain. A difference is that process models are not centred on an artefact, which could provide a certain baseline. Even though it is less explicitly discussed in the design process modelling literature, the choice of granularity is a salient problem in the area, as it can affect the behaviour of such models significantly. For instance, coarser models may combine several tasks into one, which is problematic if it obscures iteration common in the real-world process. Also, given that task sequence influences iteration, rework and thus the overall process performance, it is important for process models to capture relevant process architecture in sufficient detail without overcomplicating the model. A good example to study and illustrate granularity in the engineering design domain are network/dependency-type models, where the topic has so far received most attention. Depending on the modelling approach such models can be used in both domains and share enough properties to capture both in terms of granularity. For instance, models can capture the dependencies between components of a product or the relationships in an activity network model of a process. Due to the scope of this article, we focus on a few examples of such models, directly targeting granularity.
Noting that past research does not consider the effects of granularity on architectural analysis, Chiriac et al. (Reference Chiriac, Hölttä-Otto, Lysy and Suh2011) focus on how the degree of modularity of a product is affected by the level of granularity it is represented in. They represent a range of idealised systems and one real-world complex system in DSMs on two different levels of granularity and analyse them for their degree of modularity using three established metrics. Concluding that the results of architectural analysis can be distorted by the level of granularity of its components, they advise to be cautious when defining a particular system decomposition for analysis tasks. In a similar approach, Suh et al. (Reference Suh, Chiriac and Hölttä-Otto2015) show that the representation of a system can vary significantly depending on the system architect’s decomposition perspective, impacting on system architecture development and resulting modularity.
Cladistics is a classification method that hierarchically groups entities into discrete sets and subsets (Hennig Reference Hennig1966; ElMaraghy, AlGeddawy & Azab Reference ElMaraghy, AlGeddawy and Azab2008). It has been employed to determine an optimum granularity level for design architecture models of modular products using component-based DSMs (AlGeddawy & ElMaraghy Reference AlGeddawy and ElMaraghy2013). Cladistics analysis yields a hierarchical clustering, which can be visualised in a cladogram. For each level of this clustering a modularity index is calculated, which enables choosing the best modularity configuration and its respective granularity (AlGeddawy & ElMaraghy Reference AlGeddawy and ElMaraghy2013).
To address the need for more sophisticated product representations for architectural analysis, Tilstra, Seepersad & Wood (Reference Tilstra, Seepersad and Wood2012) present the High Definition Design Structure Matrix (HDDSM), which captures interactions between components in a product and employs a hierarchical modelling method to include higher levels of detail where needed. The approach builds upon DSM research and allows modular construction and assembly of highly detailed product models and submodels, facilitating the distribution of modelling tasks. Similar issues have been addressed in process modelling literature, where the integration of disciplines and respective process models play an important role (Grose Reference Grose1994). Tilstra et al. (Reference Tilstra, Seepersad and Wood2012) note the potential for analysis on different levels of detail with the potential of including strategic clustering.
The presented approaches show that model granularity has received increasing attention in the field of engineering design. However, while more approaches exist, especially when including ones that deal with related topics, the vast majority focuses on a particular purpose or issue and gives little attention to the wider challenges of model granularity. Also, because the contributions differ in their use of terminology, comparisons and attempts to synthesise are complicated. A clearer view of how model granularity and related challenges and opportunities can be categorised is required to advance understanding of the field and spark further, necessary discourse on the topic.
5 Different dimensions of model granularity
In simple terms, the granularity of a model is associated with the amount of detail it contains. It is, however, not immediately clear how this manifests in a model, whether different forms of granularity are conceivable and how they relate. To describe and categorise the manifestations of model granularity, a simple framework is introduced here. This requires working towards an ontological view of model granularity. In the field of modelling and simulation more generally, determining ontologies has been described as underdeveloped despite their potential benefits for the field (e.g., Hofman Reference Hofman and Tolk2012). However, it is also argued that ontology-driven approaches can mitigate challenges encountered when working with models on different levels of granularity (Benjamin, Patki & Mayer Reference Benjamin, Patki and Mayer2006). Characterising model granularity is therefore an important step towards understanding the nature of model granularity and helps to establish a vocabulary that facilitates discussions around the topic.
5.1 Synthesising relevant concepts to characterise model granularity
The structuralist view of models in philosophy of science allows to derive some insights related to model granularity. In this context a “structure
$S=[U,R]$
consists of a non-empty set
$U$
of objects (the domain of the structure), and a non-empty indexed set
$R$
of relations on
$U$
. This definition does not assume anything about the nature of the objects in
$U$
” (Frigg Reference Frigg2009). Similarly, relations do not have properties other than formal ones. While this view of models as structures falls short in describing all aspects of modelling practice in engineering design, it provides a basis for the description of model granularity. The domain (or universe)
$U$
of the structure
$S$
consists of objects, whose quantity and size depend on the degree of abstraction of the model. The number of relations is partly dependent on the degree of abstraction but also on the nature of relations they represent. Based on this, it is proposed that the structural granularity of a model describes the decomposition of model elements as well as the density of relations between them. The density here denotes the number of relations relative to the number of possible relations. This is in line with the use of the term density in complex networks and graph theory (e.g., Newman Reference Newman2003). However, reliance on density alone would be an insufficient metric as it fails to capture the internal size and information content of relations.
The structural dimension outlined in the previous paragraph does not cover information about the content and nature of granules and their interactions. Depending on the granularity of the description the variety of possible states or configurations of the model can change. In a different context, Ashby’s (Reference Ashby1956) law of requisite variety states that a control system needs a certain level of internal variety to respond to external variety, which is also relevant for the modelling domain (Conant & Ashby Reference Conant and Ashby1970). The variety of a model with a given structure can be thought of as dependent on the amount of detail in the description of its elements and their relationships. Furthermore, it is not clear how some aspects of simulation, like temporal and dynamic properties, can be accommodated. In databases, the concept of time, or temporal, granularity is used to describe how finely the time domain is represented (Bettini et al. Reference Bettini, Dyreson, Evans, Snodgrass, Wang, Etzion, Jajodia and Sripada1998). For example, the collections ‘days’, ‘weeks’, and ‘months’ are all granularities where the decomposition determines the size of the granules. Rosen, Saunders & Guharay (Reference Rosen, Saunders and Guharay2014) refer to granularity as a driver for the resolution, or complicatedness, of the response surface of the simulation. This is proportional to the number of simulation runs in the experimental design. We therefore suggest a second dimension, information granularity, which captures the intra-granule information content as well as information resolution related to analysis.
Two other important aspects that are closely related to model granularity, but do not in themselves constitute forms of granularity, are purpose and scope of a model. To a large extent they drive model granularity but do not necessarily prescribe a particular level. They influence decisions about model granularity more (scope) or less (purpose) directly and thus play an important role when discussing the topic.
5.2 A classification framework for model granularity
Model granularity can be characterised in different ways, depending on which aspects of the model are described. Figure 2 illustrates the resulting (sub-)categories in a framework based on the derivation in the previous section. On the first level it distinguishes between structural and information granularity. Structural granularity encompasses the level of (dis)aggregation of model elements. This describes the amount to which the elements in the model have been (dis)aggregated relative to the target system. A fine granularity here means that there are many little elements, whereas coarse granularity indicates fewer, bigger elements. The other type of structural model granularity concerns the relationships between those elements, which is partly dependent on their level of aggregation. However, even on a fixed level of element aggregation, the degree of description of relationships can vary. Even though these two subcategories are often not independent, they can be and describe different aspects of the model, making this distinction a sensible one.
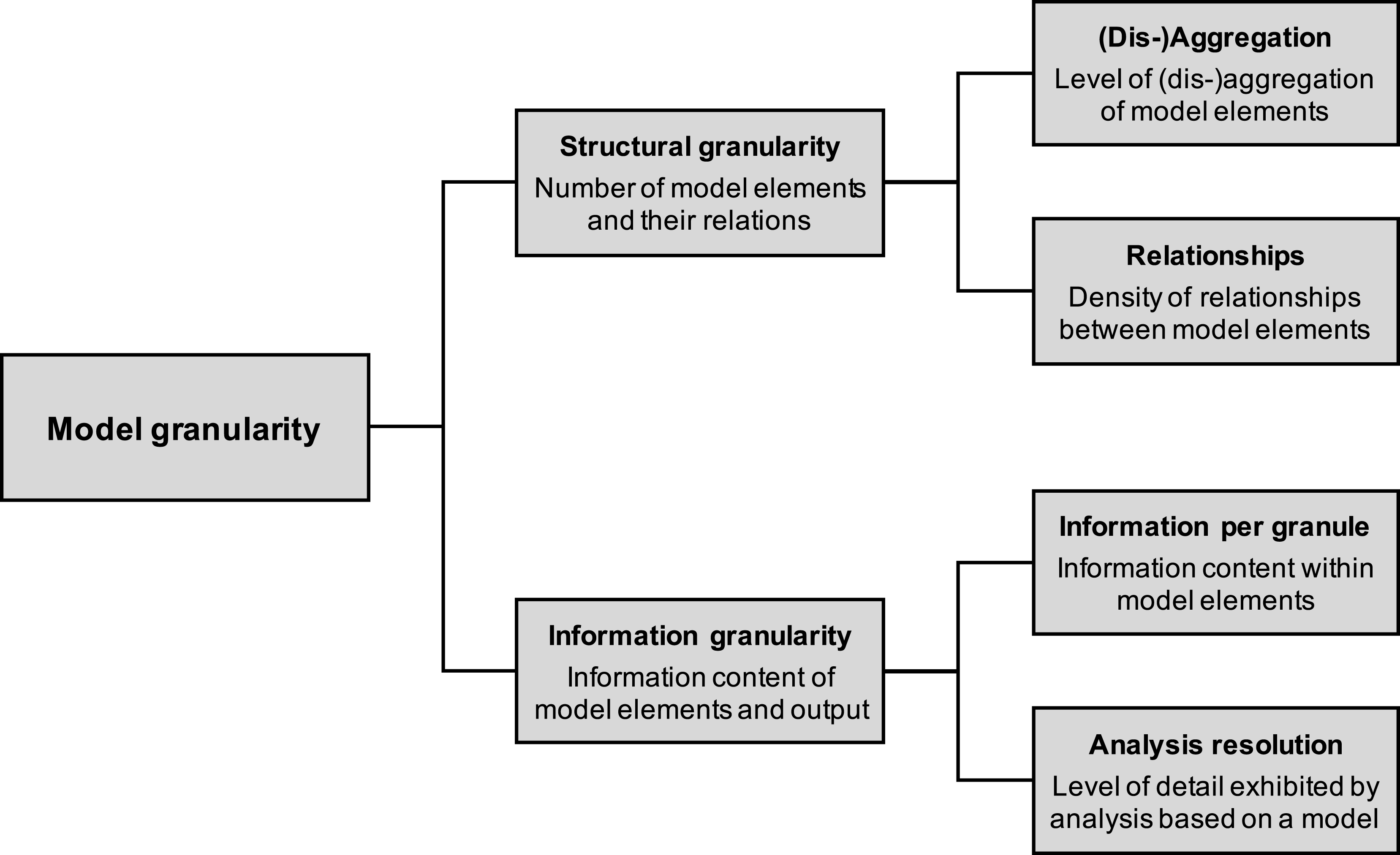
Figure 2. Different dimensions of model granularity.
Information granularity encompasses the information that is contained in the model elements, which is not taken into account by the structural part. Here, granularity relates to the type and amount of information that is associated with these elements. So, the more information content, or different types of information, are included in the model elements, the finer the information granularity within granules. Analysis resolution indicates the level of detail exhibited by analysis based on a model. This could refer to the temporal resolution of a dynamic simulation or the degree of discretisation of a process model. It is harder to define clear boundaries for analysis resolution as it partly overlaps with the other previously defined categories and relates specifically to analysis. However, given that the results obtained from simulation and other types of analysis inform decisions in many fields and engineering design in particular it is important to capture this dimension of model granularity as well. In the context of simulation modelling a related concept is model fidelity, which indicates how well it reproduces real-world behaviour. In particular, dynamic fidelity (Weisberg Reference Weisberg2007) is often proportional to the simulation resolution as it is characterised here (but also other aspects of model granularity). Nevertheless, higher simulation resolution does not automatically lead to higher model fidelity, although it might enable it in many cases.
It is important to note that these dimensions of the framework are not necessarily orthogonal. For instance, decomposing a system further leads to a finer structural granularity, which can also affect the information content of the granules. However, distinguishing between the structure and information dimension is important nonetheless because it allows to capture a wider spectrum and to account for special properties of a particular modelling approach (e.g., keeping the information content of a granule constant but disaggregating further). The two dimensions can also be traded off. For instance, the structural granularity could be increased while decreasing the information content per granule, thereby keeping the overall information content of the model constant. Generally, the degree of orthogonality between structural granularity and information granularity depends on the modelling approach (see Section 5.3 for an illustration), so both dimensions should be considered for a comprehensive characterisation of model granularity. Purpose and scope are very general considerations and affect many aspects of modelling and granularity. Even though they are not explicitly included in Figure 2, purpose and scope can influence all dimensions of granularity. The types of granularity can be said to get more specific from top to bottom.
5.3 Illustrating the classification framework
To clarify and demonstrate the concepts and framework presented in the previous section, a popular modelling approach in engineering design, the Design Structure Matrix (DSM), is used as an illustration and discussed with respect to different manifestations of model granularity. Figure 3 illustrates structural and information granularity, including the scope but not purpose. Simulation resolution, however, is not illustrated in this figure because of its dynamic nature (see Figure 4).
Figure 3. Structural and information granularity of a DSM (including scope).
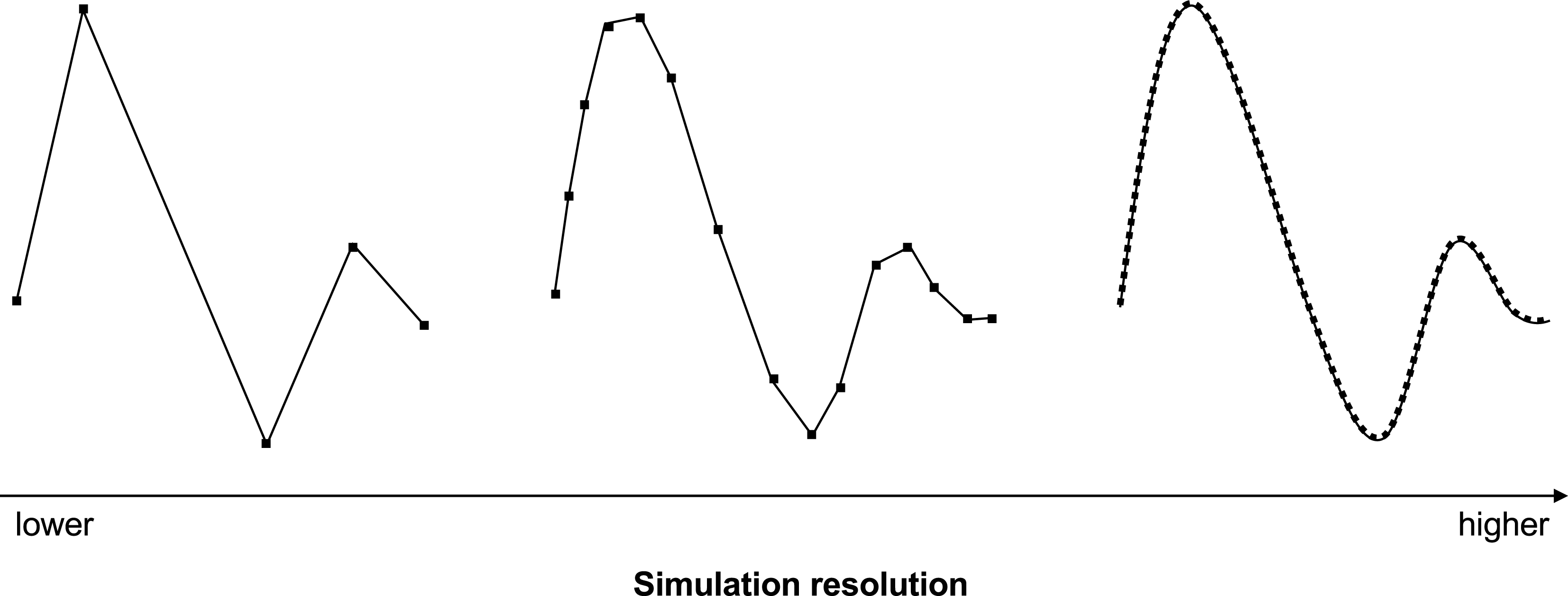
Figure 4. Temporal simulation resolution.
The two main axes in Figure 3 represent the two main aspects as discussed in the previous section and Figure 2. It is important to note that the structural granularity axis encompasses both (dis-)aggregation and relationships while the other axis only displays the information per granule (but not simulation resolution). Increasing structural granularity leads to a finer decomposition of the modelled system and more relationships between its elements. Even though these two characteristics of structural granularity are not entirely independent they do not necessarily have to correlate as displayed in Figure 3. The system boundaries stay the same unless the scope is increased or decreased, as indicated by the grey cells. This can be done irrespective of the granularity of the model. Increasing the information per granule is illustrated here by shifting from a binary dependency, to a low-medium-high indication of dependency strength and finally numeric values for two different factors. For instance, this can indicate impact and likelihood of change propagation between elements (Clarkson, Simons & Eckert Reference Clarkson, Simons and Eckert2004). Also, other types of models can be used to illustrate the concepts developed in this article. The DSM was chosen because of its simplicity and popularity in engineering design.
Figure 4 illustrates a form of simulation resolution, in particular temporal resolution. Here, a lower resolution is equivalent with fewer data points to describe system behaviour. With a higher resolution system behaviour can be described in more detail. This may yield a better description of the behaviour of the target system, although not necessarily. In any case, more data points can be used to analyse model behaviour. A higher resolution therefore means a finer granularity of the simulation output; the data granules describe a smaller fraction of the observed behaviour. The illustration here is a simple but representative example depicting a particular form of simulation resolution. Depending on the model, other forms of simulation resolution are conceivable. An example is spatial resolution, which can have a trade-off relationship with temporal resolution, for instance in particle physics. Due to the focus on models in engineering design rather than dynamic physical systems this relationship is not discussed in more detail in this article.
While an extensive demonstration of the framework to real-world models would go beyond the scope of this article, a few examples from the literature are mentioned here as a first step. The general challenge in using finished models is that the choices regarding granularity have usually already been made, concealing the underlying trade-offs. In their study on the impact of model granularity on modularity, Chiriac et al. (Reference Chiriac, Hölttä-Otto, Lysy and Suh2011) vary the structural granularity by describing the same target system with different numbers of model elements, which leads to varying amounts (and density) of dependencies between them. The modularity is also varied while keeping the granularity constant. They use only binary DSMs, so information granularity is fixed. Similarly, Tilstra et al. (Reference Tilstra, Seepersad and Wood2012) focus on structural granularity by further decomposing parts of the model, a binary DSM. Other approaches extend the information granularity, for example by assigning values for rework probability and impact to relationships between design tasks (Cho & Eppinger Reference Cho and Eppinger2005). Maier et al. (Reference Maier, Wynn, Biedermann, Lindemann and Clarkson2014) test the sensitivity of their design process simulation to different information granularities of the input model and outline in a later publication how the simulation resolution could be adjusted to account for changes in the structural granularity of the input model (Maier et al. Reference Maier, Eckert and Clarkson2015).
6 Challenges and opportunities associated with model granularity
Choices regarding model granularity present a range of challenges to modellers both conceptually and practically. However, when well understood they also offer potential opportunities regarding the modelling process and the resulting model. Based on existing research and empirical observations, four dimensions of challenges related to model granularity can be distinguished:
-
∙ Cost
-
∙ Quality
-
∙ Data
-
∙ Modelling practice
Cost is a factor that often drives decisions regarding model granularity. In many cases, building more detailed models with finer granularity or multiple levels requires more resources and time than building high-level, coarse-grained models. Related to this is the higher maintenance effort, computational requirements and reusability of specific, fine-grained models, which can lead to increased cost. However, subpar decisions made based on an insufficiently detailed model can also invoke costs, albeit not directly associated with the model itself.
A common assumption is that model quality improves with the amount of detail. This may be true in cases where model fidelity or accuracy is the principal goal (as in many simulation and analysis tasks) but it also means that the required calibration and validation become costlier and more difficult. Abstract, coarse-grained models can also offer advantages in terms of quality, if the model ought to be easily comprehensible by a wide range of stakeholders, suitable to capture a wide range of processes or provide real-time results. Both fine and coarse-grained models can thus deliver high quality outcomes, depending on the purpose of the model.
From a practical point of view data quality and availability are important factors as models are often built up on data from existing repositories. Consequently, data granulation drives model granularity to some extent. However, depending on the desired granularity of a model the available information can either be aggregated (e.g., Smirnov et al. Reference Smirnov, Reijers, Weske and Nugteren2012) or decomposed further (e.g., Alfaris et al. Reference Alfaris, Siddiqi, Rizk, de Weck and Svetinovic2010). While aggregation may require less effort and even offer opportunities such as retaining detailed information in a higher level model, mismatches in data and model granularity are generally challenging. This highlights the value of having a culture of collecting, organising and providing data for modelling purposes.
The last category refers to modelling practice more generally, including the modelling process and issues that are not directly captured by the previously introduced categories. Choosing an appropriate level of detail is one of the fundamental decisions in modelling projects (e.g., Brooks & Tobias Reference Brooks and Tobias1996), which is challenging because it can be hard to estimate their effect. Other challenges concern the model lifecycle, including reuse, compatibility, consistency with other models, usage scenarios, maintenance and stakeholders. The skill of modellers and users is another factor that has to be taken into account. In practice, the stakeholders asking for the model may also demand a certain level of detail, assuming this leads to better results.
The categories described in this section aim to give an initial overview of the challenges, but also opportunities, related to model granularity. While this may look familiar to modelling experts, such a survey can be useful for less experienced modellers and engineers, facing decisions about model granularity. A finer categorisation and more detailed description of the impact of granularity choices on particular aspects would be necessary for a more exhaustive discussion of the topic. In some cases, it may not be fully clear how the choice of a level of granularity would affect the issues mentioned as it depends on the purpose of the model and other surrounding factors how such challenges are best addressed. It is also worth noting that the overarching ‘model practice’ category encompasses challenges that may also be relevant for other categories but have wider implications and stem from the modelling process itself.
7 Discussion
The classification framework presented in Section 5 is synthesised from accepted concepts in the literature and categorises the main dimensions of model granularity. Its purpose is to define and discuss the different manifestations of granularity in models, to provide guidance to modellers and ultimately to be a reference point for future discussion around the topic. Given the sparsity of prior research on this topic in engineering design, the framework presents a first step towards tackling this challenge. As a literature review including other modelling domains reveals, related concepts have received more research attention to date. By relating the notion of granularity to these, this article provides a link that allows researchers and practitioners to draw insights from relevant discussions across a range of disciplines. The framework uncovers and addresses a number of issues surrounding model granularity and provides a basis for further research on the topic. It can support modellers in making decisions about granularity by making the different dimensions, and trade-offs between them, explicit. This also emphasises the importance of considering granularity choices in advance, as access to appropriate data and information is required throughout the modelling project. Planning a data infrastructure with awareness of granularity requirements may mitigate challenges at later stages or future modelling endeavours. Since modelling often involves several stakeholders, the framework can also help to unify perceptions of granularity. While some metrics for aspects of granularity or related phenomena exist, there is no model of the empirical relations necessary to derive meaningful measures of model granularity. The framework can serve as a basis for addressing this situation and guide the development of targeted measures in future work.
There are, however, also a number of open issues and limitations that should be considered. While the proposed categories intuitively make sense it could be argued that the framework may be architected in a different way, depending on its purpose. For instance, it could be mapped to the modelling process and the decisions to be made regarding model granularity. The choice to focus the research on model granularity is open to debate, considering the differences in terminology across disciplines. The concept of granularity is regarded as a means to unify these concepts in a coherent framework that focuses on the model itself. To clarify this and make it more explicit, the framework could be discussed in light of alternative terminologies in order to show how it relates to them. Also, the framework focuses on engineering design and is illustrated with one modelling approach from this domain. Extending this to other approaches would delimit the scope of the framework more clearly and indicate its limitations in terms of coverage.
The presented classification framework has not yet undergone extensive validation. This would include the application of the framework to a range of modelling approaches as well as empirical research into the perception of model granularity by practitioners. It can be argued that a certain face validity is given since the framework is synthesised from existing concepts. Informal discussions with modellers also suggest that it resonates with their understanding of model granularity. Proposing a terminology and classification provides a basis for further debates, ultimately contributing to its validation. Future work towards validation will thus include empirical research in the form of case studies in industrial modelling projects, including interviews and questionnaires. Additionally, a range of existing modelling approaches should be scrutinised in light of the proposed framework, thereby illustrating and validating the approach. Existing approaches could be reviewed with respect to their levels of granularity to determine how this relates to the types of problems they address.
8 Conclusions
Understanding model granularity and its implications is important for engineers who constantly make decisions based on models. While the ultimate goal is to provide recommendations for how to achieve the ‘right’ level of granularity, it is key to first understand the underlying concepts as well as how the modelling process and subsequent analysis might be impacted. The terminology and classification framework presented in this article offer a basis for further discussion and research on model granularity. Perspectives from various disciplines are integrated and synthesised, which is necessary due to the limited attention the topic has received in engineering design so far. This theoretical contribution of the article establishes the relatively abstract topic of model granularity on the research agenda. The presented framework categorises different dimensions of model granularity, principally structural and information granularity. It highlights the trade-offs modellers have to make and provides a basis for the establishment of meaningful measures of model granularity. The framework also offers support for articulating and planning granularity requirements, thereby improving modelling practice and appropriate data logistics. Even though the framework targets models in engineering design, it has bearings on the wider modelling landscape.
Further work should focus on validating the framework with modelling practitioners and testing its applicability to a range of modelling approaches. For instance, existing modelling approaches could be characterised in terms of their levels of structural and information granularity to determine what types of research questions may be addressed based on this. Additional research into the sensitivity of models and approaches to determine suitable levels of granularity is required to derive relevant recommendations for modellers. Finally, empirical investigation could reveal how related challenges are addressed in practice to date and what can be done to improve this.
Financial support
This work was supported by an Industrial CASE studentship funded by the UK Engineering and Physical Sciences Research Council and BT [EP/K504282/1].
Open access
