1 Introduction
The form of a product has a dominant effect on consumer preferences, not only in terms of aesthetics and emotional meaning, but also in the functional performance and sustainability of the product (Luchs et al. Reference Luchs, Brower and Chitturi2012). Nevertheless, when subjects have to choose between products with similar functionality and price, as in modern-day competitive markets, aesthetics become the key factor to consider (Creusen & Schoormans Reference Creusen and Schoormans2005; Kelly et al. Reference Kelly, Maheut, Petiot and Papalambros2011). In previous research, the use of two-dimensional (2D) projections has proved to be instrumental in the study of product aesthetics (MacDonald et al. Reference MacDonald, Lubensky, Sohns and Papalambros2008; Orsborn et al. Reference Orsborn, Cagan and Boatwright2009; Kelly et al. Reference Kelly, Maheut, Petiot and Papalambros2011; Lugo et al. Reference Lugo, Batill and Carlson2012, Reference Lugo, Schmiedeler, Batill and Carlson2015, Reference Lugo, Schmiedeler, Batill and Carlson2016; Valencia-Romero & Lugo Reference Valencia-Romero and Lugo2016a ). However, depth and vergence cues characteristic of three-dimensional (3D) representations are necessary for a better understanding of subjects’ perception (Pizlo Reference Pizlo2010; Higgins Reference Higgins2012). Moreover, the study of product aesthetics requires the development of more realistic and interactive surveys in order to obtain more reliable responses from subjects (Tovares et al. Reference Tovares, Boatwright and Cagan2014). These issues can be approached simultaneously with models that consider both physical dimensions and visually perceived attributes of the whole product.
Considered as aesthetic guidelines by design scientists, the Gestalt principles explain how people group distinct elements of a visual representation into greater entities and how they interpret the whole picture differently from the sum of its parts (Wertheimer Reference Wertheimer1923; Köhler Reference Köhler2015). Lugo et al. (Reference Lugo, Batill and Carlson2012, Reference Lugo, Schmiedeler, Batill and Carlson2015, Reference Lugo, Schmiedeler, Batill and Carlson2016) proposed 2D quantifications of the Gestalt principles of proximity, continuity, closure, symmetry, parallelism, and similarity in terms of design variables like lengths and ratios, and used these expressions to evaluate product aesthetics. Subsequently, Valencia-Romero & Lugo (Reference Valencia-Romero and Lugo2016a ) assessed the part-worth utilities of symmetry, parallelism, and continuity over aesthetic preferences using discrete choice experimentation (DCE), endorsing previous remarks by Jacobs (Reference Jacobs, Boyer and Sarkar2000) regarding the significance of these Gestalt principles for visual perception of continuous shapes. In addition, Valencia-Romero & Lugo (Reference Valencia-Romero and Lugo2016b ) extended the 2D quantifications of the aforementioned principles to 3D and used them as design variables for product form optimization. In this pilot study, these 3D quantifications are used to delve into the effect of symmetry, parallelism, and continuity on aesthetics.
To this end, this work features a small pilot DCE with a set of eight 3D bottle representations with combinations of two levels of symmetry, parallelism, and continuity. Subjects evaluated the designs within a virtual reality (VR) environment, thus providing them with an immersive first-person perspective and allowing them to move around and rotate the 3D product representation for a thorough exploration of the form. The VR environment was built using a commercial game engine and the immersion was achieved through a head-mounted display (HMD). The experiment in this investigation aims to test the following hypotheses.
-
(1) The quantifications of the Gestalt principles of symmetry, parallelism, and continuity for 3D representations can be used to predict subjects’ preferences regarding the aesthetics of a bottle form.
-
(2) The part-worth utility estimates of symmetry, parallelism, and continuity on subjects’ preference regarding the aesthetics of a bottle form are independent of each other.
-
(3) The aesthetic utility of each Gestalt principle does not differ significantly between women and men.
The first hypothesis implies that the mean part-worth utility estimates of each Gestalt principle are never zero throughout the population. The second hypothesis suggests that the interaction effects between symmetry, parallelism, and continuity on subjects’ preferences are negligible, and that these Gestalt principles can be considered as independent explanatory variables for the aesthetics of a bottle form. Finally, the third hypothesis suggests that female and male participants have similar aesthetic preferences for symmetry, parallelism, and continuity, with the majority of them showing either appeal or dislike for each principle.
The proposed methodology prioritizes the Gestalt principles of symmetry, parallelism, and continuity as main descriptors of the product form and focuses on bridging the gap between aesthetics and function by measuring the effect of these principles on subjects’ preferences. This investigation aims to serve as a proof of concept for future research on using the Gestalt principles as a general approach to describe the interactions between the three axes of the product design process: function, semantics, and aesthetics (see Figure 1) (Bloch Reference Bloch1995; MacDonald et al. Reference MacDonald, Lubensky, Sohns and Papalambros2008; Lugo et al. Reference Lugo, Batill and Carlson2012; Homburg et al. Reference Homburg, Schwemmle and Kuehnl2015; Valencia-Romero & Lugo Reference Valencia-Romero and Lugo2016b ). In this framework, aesthetics is sustained by function and semantics through the product form or Gestalt, while the latter two are respectively linked to aesthetics through the interaction between the product’s dimensional variables and their effect on subjects in their first impression. Likewise, the emotional bond between subject and product, which is characterized by specific semantic codes, provides designers with enriching feedback about the product Gestalt, ultimately leading to improvements in performance and appearance (Parr Reference Parr2003; Lawson Reference Lawson2006).
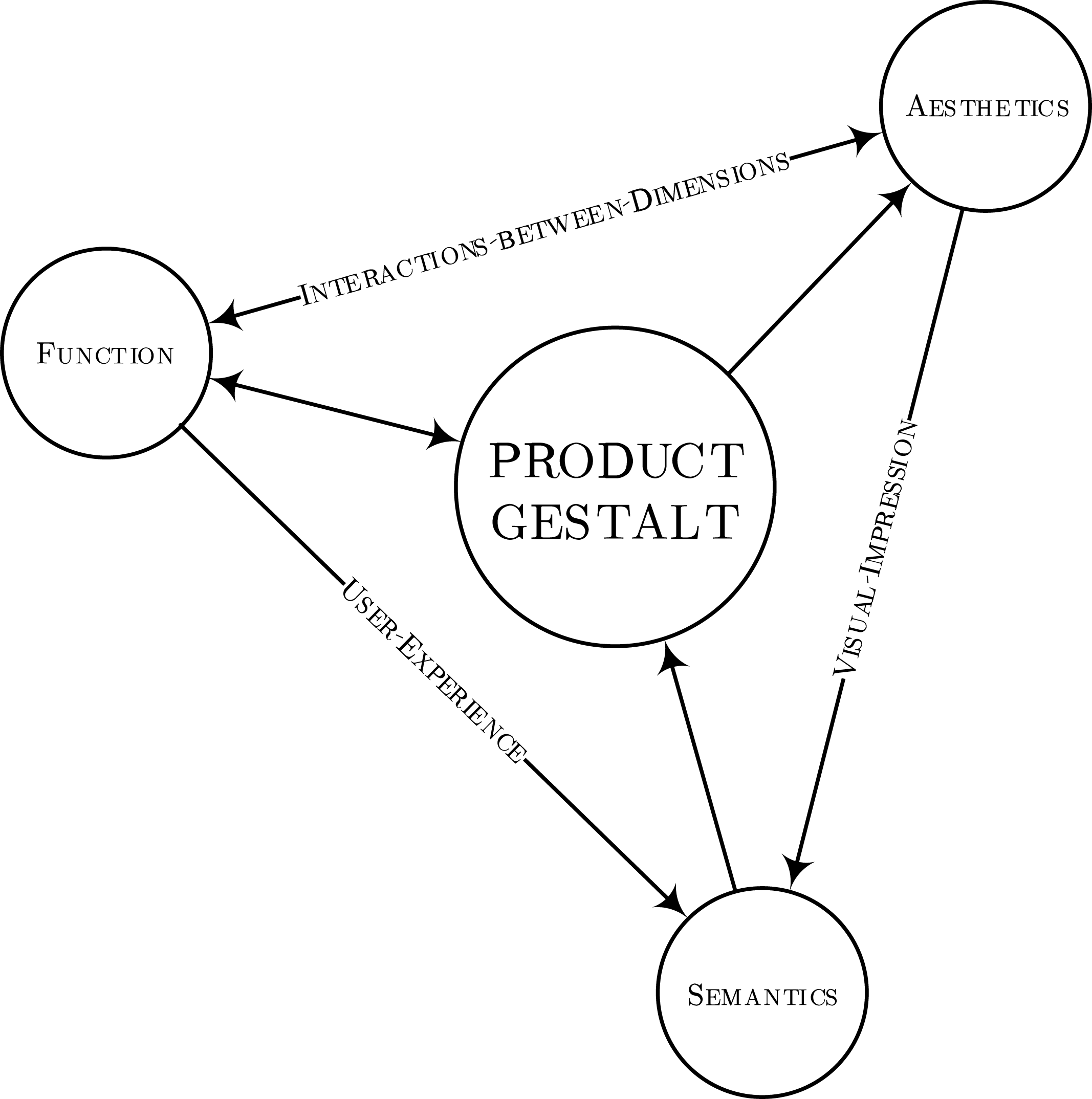
Figure 1. The three axes of the design process with product form as nucleus (Homburg et al. Reference Homburg, Schwemmle and Kuehnl2015). This work prioritizes the Gestalt principles as main descriptors of the product form and focuses on bridging the gap between aesthetics and function by measuring the effect of these principles on subjects’ preferences.
The following section provides background on the use of VR as a tool in the assessment of product aesthetics. Section 3 describes the methodology, with each subsection covering a step in the use of 3D quantified Gestalt principles in conjunction with VR technologies for elicitation of aesthetic subject preference. The case study of a 3D representation of a bottle using the proposed methodology and DCE methods is presented in Section 4, with analysis and discussion of results provided in Sections 5 and 6, respectively. Finally, conclusions are given in Section 7.
2 Background
A brief review concerning recent work on Gestalt principles and VR technologies in product aesthetics is presented next. The reader should refer to Biocca & Levy (Reference Biocca and Levy1995), Wagemans et al. (Reference Wagemans, Elder, Kubovy, Palmer, Peterson, Singh and von der Heydt2012a ,Reference Wagemans, Feldman, Gepshtein, Kimchi, Pomerantz, van der Helm and van Leeuwen b ), Jerald (Reference Jerald2016), and Lugo et al. (Reference Lugo, Schmiedeler, Batill and Carlson2016) for further information.
2.1 Gestalt principles in product aesthetics
Formally known as ‘laws of organization in perceptual forms’ (Wertheimer Reference Wertheimer1923), the Gestalt principles are regarded as standards for visual appeal by researchers in areas related to human-centered design. The word ‘gestalt’ literally translates as ‘shape’ from German, and it is a synonym of ‘unity’ and ‘coherence’ when used with the initial letter capitalized within the context of aesthetics. The notion of unity has been addressed by Post et al. (Reference Post, Blijlevens and Hekkert2016), who used pictures of four different product categories to study form unity and variety, their effect on people’s aesthetic judgments, and possible correlations between these two attributes. In Post et al.’s work, the ‘unified’ and ‘variegated’ designs were classified, respectively, in terms of the classical Gestalt principle of symmetry and its counterpart asymmetry, and other visual properties like color and contrast. Although having opposite meaning, the results suggest that the harmony between unity and variety can enhance visual appeal, since both characteristics were found to have a positive effect on aesthetics, with symmetric designs being more important.
Symmetry does not always have a desirable influence on subjects’ preferences. As reported in Bajaj & Bond’s (Reference Bajaj, Bond, Batra, Seifert and Brei2015) and Stamatogiannakis et al.’s (Reference Stamatogiannakis, Luffarelli, Yang, Batra, Seifert and Brei2015) works, the excessive use of symmetry in advertising artwork could ‘backfire’ when intended to cause excitement in users, notwithstanding its status as a badge of elegance within design science. While perfect symmetry can be considered as ‘boring’, the use of asymmetric forms could provoke ‘amusement’ in subjects whenever it embodies a decipherable meaning (Kumar Reference Kumar, Batra, Seifert and Brei2015). In other words, as inferred from Leyton’s (Reference Leyton2012) work, only asymmetries can tell stories (i.e. first fundamental law of memory storage). From an atomistic perspective, the presence of asymmetric elements in a visual representation is considered a ‘lack of balance’ (Bradley Reference Bradley2013). Yet, from a Gestalt perspective, asymmetry can be used to provide dynamic balance, and thus unity, to the whole form (Post et al. Reference Post, Blijlevens and Hekkert2016). It is not a trivial matter to treat both the unity/symmetry and variety/asymmetry issues simultaneously, since the latter lack first-hand dimensional references (e.g. mirror planes, rotation axes) that could facilitate their analysis. For this purpose, it is necessary to integrate other visual properties that account for the variety in shape along a visual representation.
The Gestalt principles of parallelism and continuity could aid in explaining the unity versus variety trade-off. Parallelism is the tendency to group elements by their similarity in direction or orientation, and it can sometimes be considered as a special case of translational symmetry (Pomerantz & Cragin Reference Pomerantz, Cragin and Wagemans2015). For continuous shapes, parallelism could be estimated in terms of the differences in slope between segments of equal extension in a particular direction (Valencia-Romero & Lugo Reference Valencia-Romero and Lugo2016a ). Under this definition, the condition of no parallelism is equivalent to perpendicularity, and can serve as a complement to estimate the asymmetry between elements. On the other hand, the principle of continuity or ‘good continuation’ explains the grouping of consecutive elements with smooth changes between them. This principle has been associated with curvature (Singh & Fulvio Reference Singh and Fulvio2007; Bertamini et al. Reference Bertamini, Palumbo, Gheorghes and Galatsidas2016), with the description of maximum continuity given to flat elements, which have zero curvature (Valencia-Romero & Lugo Reference Valencia-Romero and Lugo2016b ).
Previous efforts in the development of models that effectively characterize how each of the Gestalt principles mentioned above, along with other supporting visual properties, influence subjects’ perception about a product form have been documented. Lo et al. (Reference Lo, Ko and Hsiao2015) proposed quantifications of balance, equilibrium, symmetry, proportion, unity, and minimalism as measures of aesthetic appeal on a zero-to-one scale and – using all-in-one stereos as a case study – correlated the weighted average between these expressions and subjects’ aesthetic preferences to optimize the shape of the stereo that obtained the lowest aesthetic evaluations. Crăciun et al. (Reference Crăciun, Rusu and Tudose2015a ,Reference Crăciun, Rusu and Tudose b ) used evolutionary algorithms to generate vase shapes parametrized with Bézier curves and circular arcs with proportions equal to the golden and harmonic sections, and conducted a survey on which subjects rated these shapes in terms of perceived beauty, harmony, or artistry. More recently, Valencia-Romero & Lugo proposed quantifications of the Gestalt principles of symmetry, parallelism, and continuity for 2D (Reference Valencia-Romero and Lugo2016a ) and 3D (Reference Valencia-Romero and Lugo2016b ) representations (see Table 1) and used them as design variables for shape optimization. These models allow designers to delve into aesthetics thanks to the possibility of designing orthogonal and efficient preference experiments in which the stimuli are product forms with specific combinations of these visual properties.
2.2 Virtual reality in product aesthetics
Virtual reality is often considered by the general audience as a type of media (like radio or television), or as a collection of several technologies (software, hardware). However, VR is better defined in terms of human experience as a ‘real or simulated environment in which a perceiver experiences telepresence or mediated perception of an environment’ (Steuer Reference Steuer, Biocca and Levy1995). In this sense, a VR system is characterized in terms of its capabilities of immersion (perception of an artificial world), interaction with the environment, and presence or feeling of physically being in the environment (Wloka Reference Wloka, Rix, Haas and Teixeira1995). This concept makes VR an entire science centered in the human being and allows professionals from other fields of knowledge – such as psychology, computer science, and engineering design – to build new research areas upon the capabilities of VR systems to explore human perception.
The introduction of VR-based methodologies to early stages of the product development process has been favored mainly by their increasing affordability (Aromaa and Väänänen Reference Aromaa and Väänänen2016; Hilfert & König Reference Hilfert and König2016), with recent research strongly focused on overcoming implementation challenges in academia and industry (Pérez Fernández & Alonso Reference Pérez Fernández and Alonso2015; Sacks et al. Reference Sacks, Whyte, Swissa, Raviv, Zhou and Shapira2015; Huang et al. Reference Huang, Liaw and Lai2016; Lawson et al. Reference Lawson, Salanitri and Waterfield2016). The range of application of VR systems is practically unlimited; for instance, collaborative design (Koutsabasis et al. Reference Koutsabasis, Vosinakis, Malisova and Paparounas2012), evaluation of user experience (Rebelo et al. Reference Rebelo, Noriega, Duarte and Soares2012), and architectural planning (Portman et al. Reference Portman, Natapov and Fisher Gewirtzman2015) are some of the most relevant applications of VR for designers. Thanks to current VR systems’ immersing and rendering capabilities, designers can develop more realistic scenarios to elicit subjects’ stated preferences via DCE or conjoint experiments.
In previous research, Tovares et al. (Reference Tovares, Boatwright and Cagan2014) applied conjoint analysis to study aesthetic preference for 2D, virtual, and actual coffee mugs, with their results showing that subjects’ judgments about the VR prototypes were more similar to those about the actual mugs than the ones using 2D static representations. Similarly, Backhaus et al. (Reference Backhaus, Jasper, Westhoff, Gausemeier, Grafe and Stcklein2014) proposed a three-stage VR-based conjoint analysis methodology, with the participation of both the subjects and the design team, evaluating several product attributes within a VR environment created with a commercial game engine.
Table 1. Quantification of symmetry, parallelism, and continuity for 3D representations (Valencia-Romero & Lugo Reference Valencia-Romero and Lugo2016b )
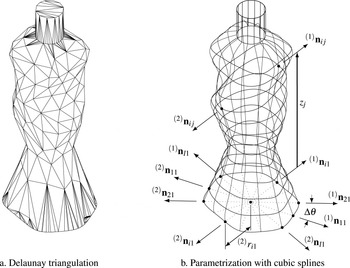
Figure 2. Examples of discretization of a 3D bottle representation.
In the development of VR-based scientific applications, the use of commercial game engines is preferred over existing computer-aided design (CAD) platforms due to the limited compatibility of the latter with VR systems (Friese et al. Reference Friese, Herrlich, Wolter, Ciancarini, Nakatsu, Rauterberg and Roccetti2008; Kosmadoudi et al. Reference Kosmadoudi, Lim, Ritchie, Louchart, Liu and Sung2013). It is the connection between VR and the video game industry that has been key to the development of more immersive visualization technologies. Commercial game engines provide templates and assets for VR that require minimum customization and coding, and can be used for experimentation with subjects. In general, the visual assessment of products in VR environments benefits designers through the reduction of prototyping costs thanks to the versatility and user-friendliness of these applications (Bordegoni Reference Bordegoni, Monica and Rizzi2011).
3 Methodology
The methodology herein is built upon previous work by Valencia-Romero & Lugo (Reference Valencia-Romero and Lugo2016a ,Reference Valencia-Romero and Lugo b ). First, the product form is discretized in a convenient way, such that the Gestalt quantifications of symmetry, parallelism, and continuity (see Table 1) can be applied in a common unit range, making them easy to manipulate. Then, the model is used to generate product forms with different combinations of perceivable low and high Gestalt values following an experimental design for preference elicitation. Finally, subjects are invited to evaluate the product forms they consider to be most aesthetically appealing in terms of binary choices while immersed in the VR environment. This procedure is described next using a 3D generic bottle representation as an example and Gestalt quantifications for symmetry, parallelism, and continuity with cylindrical coordinates (see Figure 2(b)).
3.1 Product form discretization and Gestalt quantification
Prior to calculating the Gestalt values, the 3D representation of the product form has to be simplified to its most latent geometric attributes using discretization techniques. For instance, to compute the values of symmetry (Eq. (1)) and parallelism (Eq. (2)) of the 3D bottle representation shown in Figure 2 using cylindrical coordinates, the model must allow designers to query radius values
$\text{}^{(\ast )}r_{ij}$
and normal vectors
$\text{}^{(\ast )}\mathbf{n}_{ij}$
, at
$i=1,2,\ldots ,I$
opposite azimuthal coordinates
$\text{}^{(1)}\unicode[STIX]{x1D703}_{i}$
and
$\text{}^{(2)}\unicode[STIX]{x1D703}_{i}$
(
$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D70B}/I$
rad), and
$j=1,2,\ldots ,J$
heights
$z_{j}$
(directly from the model or by interpolation). The number of individual Gestalt quantifications is
$I\times J$
. For continuity, the model must also expedite the computation of the Gaussian curvature
$K_{ij}$
. More precisely, the estimation of second derivatives to calculate the principal curvatures is required.
The designer might consider the use of CAD software in the sketching and/or final rendering of the discretized model. Contemporary CAD tools are capable of managing different discretization techniques – like Delaunay triangulation (see Figure 2(a)) and parametrization with cubic splines (see Figure 2(b))—that provide complete information about coordinates, normal vectors, and Gaussian curvature at any point of the form surface. From the two 3D bottle models shown in Figure 2, the discretization using cubic splines is more computationally efficient if implemented in numerical analysis software. The availability of interpolation libraries for scientific programming makes estimation of the cubic spline model and its first and second derivatives more straightforward. Moreover, if rails and cross sections are orthogonal at each knot, the computation of the principal curvatures using Eq. (4) does not require an additional local parametrization, and
$\unicode[STIX]{x1D705}_{1}$
and
$\unicode[STIX]{x1D705}_{2}$
become the elements of the diagonal of the shape tensor. Finally, the rendering of the cubic spline model with loft operations available in CAD software is smoother, with the Delaunay triangulation model requiring large arrays of vertices (fine meshing) to properly recreate the actual form, a condition that is counterproductive if further form optimization of the model is required.
3.2 Generation of product forms based on Gestalt values
The discretized model and all of the functions necessary to quantify the Gestalt principles are integrated into an optimization algorithm to generate product forms with particular Gestalt values. The optimization problem (see Eq. (5)) combines average measures of symmetry (
$\bar{s}_{ij}$
), parallelism (
$\bar{p}_{ij}$
), and continuity (
$\bar{c}_{ij}$
) across coordinates
$(i,j)$
in a scalar merit function and, depending on whether the sign of one of the exponents
$u$
,
$v$
, and
$w$
is positive or negative, searches the radius values
$\text{}^{(\ast )}r_{ij}$
that minimize or maximize, respectively, each Gestalt principle:
$$\begin{eqnarray}\displaystyle \min _{\text{}^{(\ast )}r_{ij}}(\bar{s}_{ij})^{u\,}(\bar{p}_{ij})^{v\,}(\bar{c}_{ij})^{w},\quad u,v,~\text{and}~w\in \mathbb{R} & & \displaystyle \nonumber\\ \displaystyle \text{s.t.}\left\{\begin{array}{@{}l@{}}\text{Dimensional}~\text{constraints}\quad \\ \text{Functional}~\text{constraints}\quad \\ \text{Behavioral}~\text{constraints}~\text{on}~\bar{s}_{ij},\bar{p}_{ij},\text{and}~\bar{c}_{ij}.\quad \end{array}\right. & & \displaystyle\end{eqnarray}$$
For the case of a bottle form, the dimensional constraints define the range of possible radius values across the vertical and azimuthal axes, while the functional constraints could be the bottle capacity and/or the amount of material. Functions that measure the complexity of the model and the manufacturing costs can also be included. The behavioral constraints are used to define the range of desired Gestalt values, their variability, and distribution along the product form.
Using sequential quadratic programming (SQP), the optimization problem from Eq. (5) is applied to the discretized 3D bottle model with cubic splines shown in Figure 2(b) to generate a set of bottle designs with combinations of low and high values of each Gestalt principle (full factorial design with
$K=3$
two-level attributes resulting in
$2^{K}=8$
bottle forms). The list of parameters and constraints considered to run the algorithm is summarized in Table 2. The number of design variables used in the optimization problem is
$I\times (J-1)=182$
(the last cross section corresponds to the bottom radius of the bottle tap,
$\text{}^{(\ast )}r_{iJ}$
, which is constant). The definition of these parameters required several iterations, which ultimately served to distinguish the low and high Gestalt values for which the generation of bottle forms with even combinations of symmetry, parallelism, and continuity was feasible. Finally, the bottle forms generated with their respective Gestalt values and capacities in liters are shown in Table 3b–c. To the best of the authors’ knowledge, these bottle forms are original and do not resemble available products in the marketplace.
Table 2. Parameters considered in the generation of bottle forms using SQP on Eq. (5) and the parametrization with cubic splines shown in Figure 2(b)
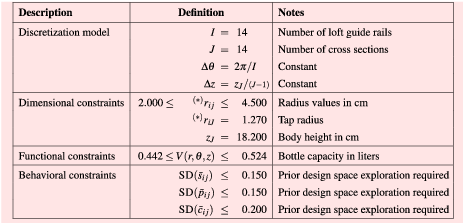
Table 3. Full factorial set of bottle forms for the pilot DCE and simulated population-level choice probabilities
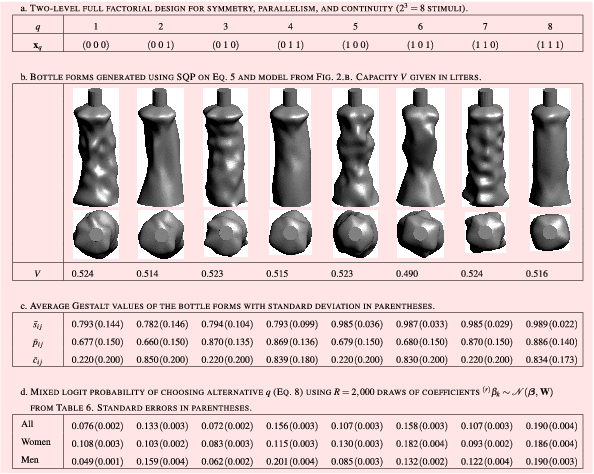
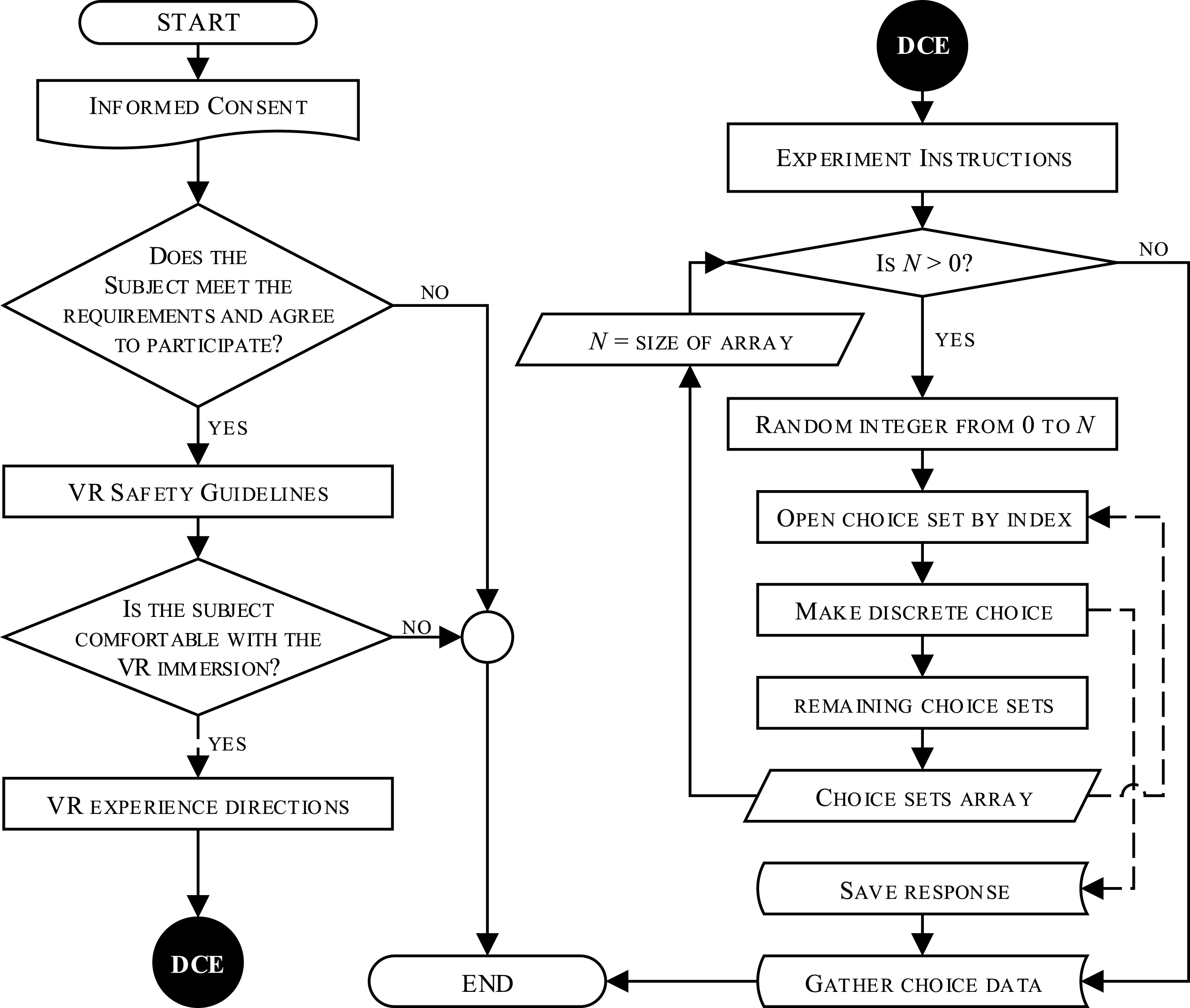
Figure 3. Immersive virtual DCE study procedure.
3.3 Elicitation of aesthetic preference with VR prototypes
Evaluation of the relationship between Gestalt principles and aesthetic preference requires experiments in which subjects can visually interact with a finite number of 3D product representations from an orthogonal and balanced set of combinations of Gestalt values. To properly test main and cross effects of the Gestalt quantifications, the experiment should also allow subjects to distinguish the designs they consider more aesthetically appealing from those they dislike. Both issues can be addressed with preference elicitation methods like rankings/choice-based conjoint analysis and DCE (Louviere et al. Reference Louviere, Flynn and Carson2010), used in previous research for evaluation of aesthetic subject preference for 2D and 3D product representations (Orsborn et al. Reference Orsborn, Cagan and Boatwright2009; Tovares et al. Reference Tovares, Boatwright and Cagan2014; Valencia-Romero & Lugo Reference Valencia-Romero and Lugo2016a ).
The integration of VR technologies for elicitation of aesthetic preference allows designers to test close interactions between subject and product form without the need to manufacture actual prototypes, thus minimizing costs and bias due to physical contact (Ferrise et al.
Reference Ferrise, Bordegoni and Cugini2013). Another advantage of using VR systems in preference studies is the automation of the experiment. For a VR-based DCE, the presentation of choice sets and the recording of subjects’ responses can be performed automatically without the need for further intervention of the designers. An immersive VR-based DCE with
$N$
choice sets using VR systems is described in Figure 3. This procedure is applied in the next section to determine the part-worth utility estimates of the Gestalt quantifications on subjects’ preferences about the aesthetics of the bottle forms shown in Table 3b. Since each of the Gestalt quantifications (i.e.
$\bar{s}_{ij}$
,
$\bar{p}_{ij}$
, and
$\bar{c}_{ij}$
) take into account the whole product form, it is sufficient to model the product preference as a linear-additive model of only the Gestalt quantifications.
4 Virtual DCE for the aesthetics of a bottle
4.1 Development of the VR environment
The VR environment to conduct DCE was created using the game development middleware Unreal Engine 4.10 (UE4), developed by Epic Games, Inc. (2014). The game logic within the UE4 platform was mainly developed through the ‘Blueprint’ visual scripting system, allowing for rapid development and understanding of the tool. The VR-based DCE project was created in UE4 using the ‘first-person’ Blueprint template, with most of the assets used for the construction of the DCE scenario created in Autodesk 3ds Max academic version (Autodesk, Inc. 2016) and imported as Filmbox .fbx files.
The visualization of the VR environment was made through the Oculus Rift Development Kit 2 (Oculus VR, LLC 2014) HMD. Prior to the immersion, the subjects received instructions about the use of the game controller, a Logitech F710 (Logitech International S.A. 2016). Only three buttons (including the start button) and the two joysticks were configured to provide commands for showing instructions, moving around, and rotating/selecting objects (see Figure 4). The virtual DCE environment consisted of four stages, with additional audio instructions in every scene. At the beginning, subjects were on a flat roof at an elevated height on which they found a board with a welcome message (see Figure 5(d)). In this stage, subjects were asked to try the game controller (see Figure 4(b)–(d)) and move around the scene, and walk through a door which would redirect them to the next stage. The second stage was a training exercise which consisted of two rectangular cuboids on a table that served as a mock-up of the DCE (see Figure 5(e)). On the front and back walls, subjects would find more instructions on the use of the controller to rotate and select the object they preferred (see Figure 4(e)). In the third stage, subjects would find a progress bar and would be asked to rotate each product representation and select the one they found more appealing (see Figure 5(f)–(h)). At the end of the DCE, subjects would be redirected to the first scenario (see Figure 5(i)).
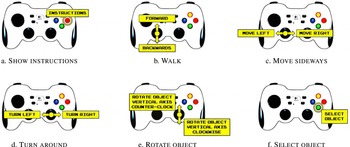
Figure 4. Game controller instructions for the virtual DCE study.
Figure 5. Highlights from the virtual DCE.
4.2 Experimental procedure
Figure 3 summarizes the steps to conduct the virtual DCE, from the informed consent process to the gathering of choice data. The set of 3D bottle representations presented in Table 3 was used in a two-alternative, full-profile DCE – i.e.
$N=\binom{8}{2}=28$
choice sets in all – using the VR environment previously described. The experiment was given approval by the Institutional Review Board of the University of Puerto Rico–Mayagüez Campus and was restricted to participants who were 21 years of age or older with normal vision without spectacles. Handbills, social networks, and emails were used to invite the student community to participate in the experiment, with no compensation offered. Each subject was introduced to the VR facility and was given a description of the experiment and risks. Next, the subjects were asked to carefully read the informed consent form and sign it if they agreed to participate.
Before beginning the experiment, each subject was given guidelines on how to safely wear the VR headset. The display was then switched on, and a demonstration scene was presented to the subject in order for them to adjust the lenses, making sure that they could see the environment clearly. Finally, the virtual DCE environment was initialized, starting with the training section in which the subjects received directions for the experiment and the use of the game controller. The purpose of the training section and the instructions was to prompt users to move around properly within the VR environment in order to minimize the risk of dizziness (also known as VR sickness).
When the subjects felt comfortable with the HMD and had completed the training section, they were asked to press start to begin the DCE survey. Then, a random choice set of bottles was presented and they were asked to rotate each one and pick the one they found more appealing; the latter action reset the subject’s position within the environment and introduced a different choice set from the 27 remaining, and so on. The rotation command acted upon the bottle that was closest in proximity. At all times, the subjects were able to zoom in on each bottle by physically moving their heads forward (see Figure 5(h)). Halfway through the experiment, at the end of the 14th choice set, the paused message was shown (see Figure 5(g)) and the subject had the opportunity to remove the head-mounted display and rest for a couple of minutes. Back in the experiment, and after completing the 28 choice sets, a ‘thank you’ message was shown (see Figure 5(i)).
4.3 Utility model for the DCE analysis
The choice data are analyzed with standard and random-parameter (mixed) logit regression using hierarchical Bayes estimation and Metropolis–Hastings sampling (Train Reference Train2006). Here, it is assumed that the aesthetic utility of person
$n$
from alternative
$q$
is equal to the sum of the products between the part-worth aesthetic utility of each Gestalt quantification,
$\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}$
, and the corresponding level of each principle,
$[\mathbf{x}_{q}]_{k}\in \{0,1\}$
(see Table 3a):
$$\begin{eqnarray}U_{nq}=V_{nq}+\unicode[STIX]{x1D716}_{nq}=\left(\mathop{\sum }_{k=1}^{K}\,\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}[\mathbf{x}_{q}]_{k}\right)+\unicode[STIX]{x1D716}_{nq},\end{eqnarray}$$
where
$V_{nq}$
is the representative utility and
$\unicode[STIX]{x1D716}_{nq}$
is the portion of
$U_{nq}$
that is not assessed by the model. For logit, the probability (conditional on
$\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}$
) that person
$n$
chooses design
$q\in Q$
can be computed as (Train Reference Train2009; Kuhfeld Reference Kuhfeld2010)
$$\begin{eqnarray}L_{nq}(\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k})={\displaystyle \frac{\exp (V_{nq})}{\mathop{\sum }_{q^{\prime }=1}^{Q}\exp (V_{nq^{\prime }})}}.\end{eqnarray}$$
In standard logit, the estimates of
$\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}$
are assumed to be the same for every person. For the mixed logit, these part-worth utility estimates are assumed to be multivariate normally distributed throughout the population with mean vector
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
and covariance matrix
$\mathbf{W}$
. The latter model allows the researchers to estimate
$\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}$
for every person and assess interactions between explanatory variables (Train Reference Train2009). The simulated population-level probability that any person chooses alternative
$q$
from set of designs
$Q$
can be calculated as
$$\begin{eqnarray}\text{Pr}(q|Q)={\displaystyle \frac{1}{R}}\mathop{\sum }_{r=1}^{R}L_{nq}(\text{}^{(r)}\unicode[STIX]{x1D6FD}_{k}),\end{eqnarray}$$
where
$\text{}^{(r)}\unicode[STIX]{x1D6FD}_{k}$
is constant for standard logit and is sampled from
$\mathscr{N}(\boldsymbol{\unicode[STIX]{x1D6FD}},\mathbf{W})$
for mixed logit (Train Reference Train2009).
4.4 Limitations of the pilot study
The pilot study presented here evaluates the effects of low and high values of symmetry, parallelism, and continuity on aesthetic subject preference for a particular 3D product representation, in accordance with the baseline Gestalt theory (Wertheimer Reference Wertheimer1923). In other words, the investigation only tests perceivable differences in visual grouping of the aforementioned principles and does not aim to identify what the optimum values of Gestalt for the case study are. On the other hand, this approach makes the full-profile DCE using VR technologies manageable in size and less taxing for the subjects. The nature of the experiment limits the sourcing of participants in a timely fashion, thus making it difficult to obtain sufficient samples to assess higher levels of interaction and analyze the effect of attributes such as age, genre, and professional background. The potential for expansion of the methodology proposed lies in addressing these issues.
5 Results and analysis of choice data
5.1 Experimental results
In total, 21 women and 21 men agreed to participate. None of the subjects had previously experienced VR, which served as a main motivator for their participation in the DCE. The average durations of the training section and DCE survey for women and men are presented in Table 4. Overall, the training section was completed in approximately 3 min, while the DCE survey section took around 8 min. Although most of the participants had previously interacted with computer-simulated graphics like those of CAD software and video games, some reported having felt dizzy at different moments during the VR experience. This caused a reduction in the interaction time between subjects and the bottle forms for the last choice sets in the DCE, which could have affected their judgment.
Table 4. Average durations of the virtual DCE experiment. Standard deviation values are given in parentheses
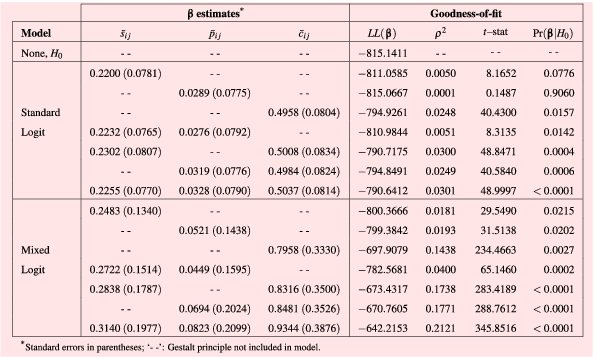
Table 5. Estimates and goodness-of-fit tests for different logit models applied to the case study
5.2 Simulation of logit models via hierarchical Bayes
The population-level part-worth utility estimates,
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
, for the standard and mixed logit models with several conditions of interests and corresponding goodness-of-fit statistics are shown in Table 5. The models are compared using the likelihood ratio index
$\unicode[STIX]{x1D70C}^{2}$
(sometimes called McFadden’s pseudo-
$R^{2}$
) (McFadden Reference McFadden and Zarembka1974; Train Reference Train2009; Mokhtarian Reference Mokhtarian2016) and the
$t$
-statistic against the ‘no model’ condition (i.e. global null hypothesis,
$H_{0}:|\boldsymbol{\unicode[STIX]{x1D6FD}}|=\mathbf{0}$
). Unlike the
$R$
-squared statistic used in linear regression, the likelihood ratio index does not have interpretable meaning for values between 0 (useless model) and 1 (perfect, likely impossible fit), but the model with greater
$\unicode[STIX]{x1D70C}^{2}$
value fits the data better (Train Reference Train2009). For the case study, the mixed logit model that considered all of the Gestalt principles in the simulation had the greatest
$\unicode[STIX]{x1D70C}^{2}$
value, followed by the mixed model without symmetry. In general, the results suggest that continuity is the most critical explanatory variable and that the model’s likability benefits from including symmetry and parallelism. The probability values of these models with respect to the ‘no model’ condition were low, suggesting that the global null hypothesis that the part-worth utility estimates of the Gestalt principles are zero can be rejected. On the other hand, the standard logit models obtained low
$\unicode[STIX]{x1D70C}^{2}$
values, with only the versions with all parameters and with continuity overcoming the null hypothesis.
The results of the mixed logit model (including estimates of
$\mathbf{W}$
) with the greatest likelihood ratio index are presented in full in Figures 6–7 and Tables 6–8. Figure 6 shows the distribution of each of the part-worth utility estimates throughout the sample (number of bins:
$\lceil \sqrt{42}\rceil =7$
) with fit of the normal distribution density functions to the data according to the assumptions of the mixed logit model. The standard deviation values, along with shares of the sample that placed a negative (
$\unicode[STIX]{x1D6FD}_{k}<0$
) or null (
$\unicode[STIX]{x1D6FD}_{k}=0$
) value on each principle, are shown in Table 6, while covariance and correlation among estimates are presented in Tables 7 and 8, respectively. The results of the simulated mixed logit probability of choice for each bottle using Eq. (7) are shown in Table 3d, with bottle
$q=8$
having the greatest overall aesthetic representative utility.
The obtained population-level
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
estimates for cylindrical symmetry, parallelism, and curvature-based continuity were 0.3140, 0.0823, and 0.9344, respectively. In the case of symmetry, 62.15% of its part-worth utility in
$R=2,000$
draws from
$\mathscr{N}(\boldsymbol{\unicode[STIX]{x1D6FD}},\mathbf{W})$
is above zero (see Table 6, values of
$\text{Pr}(\unicode[STIX]{x1D6FD}_{k}<0)$
), suggesting that this Gestalt principle is a positive inducement of aesthetic preference for bottle forms. Similarly, approximately two-thirds of the subjects apparently prefer a high level of continuity, whose estimate is approximately three times greater than the effect of low or high symmetry and seven times the estimate of parallelism. There is relatively little skewness in the distribution of simulated individual part-worth utilities
$\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}$
of symmetry and parallelism, as seen in Figure 6(a)–(b). Regarding the latter, preference appears to be nearly halved (45.60% of the estimates are below zero), contrasting with the rejection of the null hypothesis that this estimate is zero from Table 5. On the other hand, Figure 6(c) shows that the distribution of estimates for continuity is left-tailed, suggesting that its aesthetic utility tends to be positive (concentrated to the right).
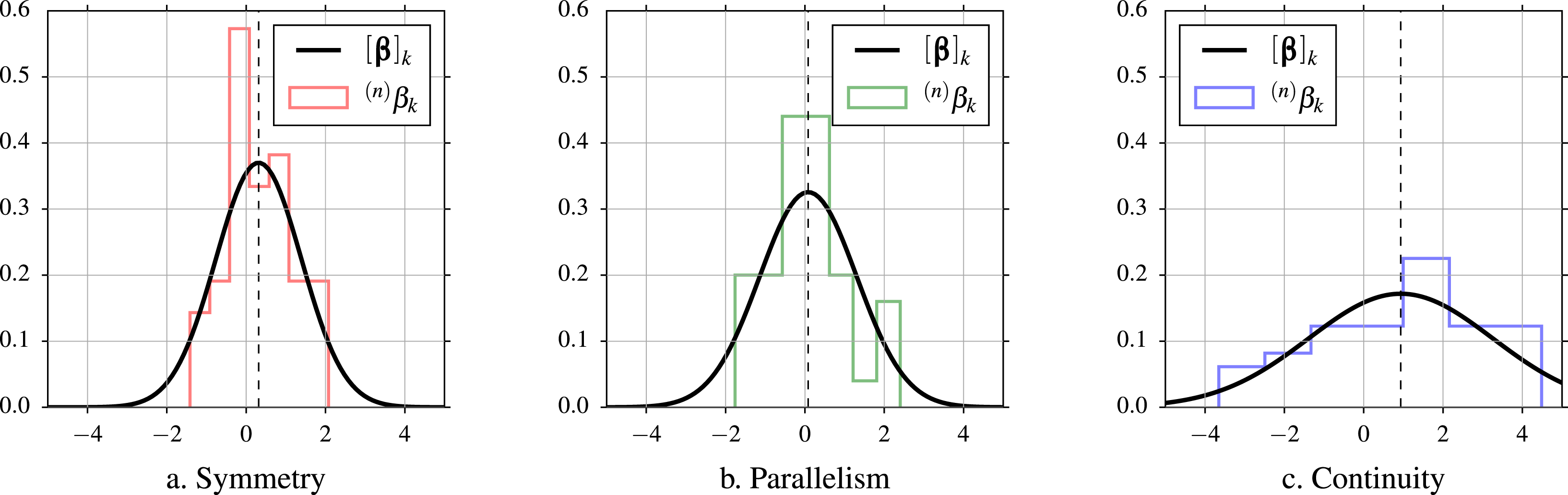
Figure 6. Population-level estimates
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
and normalized count of individual part-worth aesthetic utility estimates
$\text{}^{(n)}\unicode[STIX]{x1D6FD}_{k}$
of symmetry, parallelism, and continuity for a 3D bottle representation.
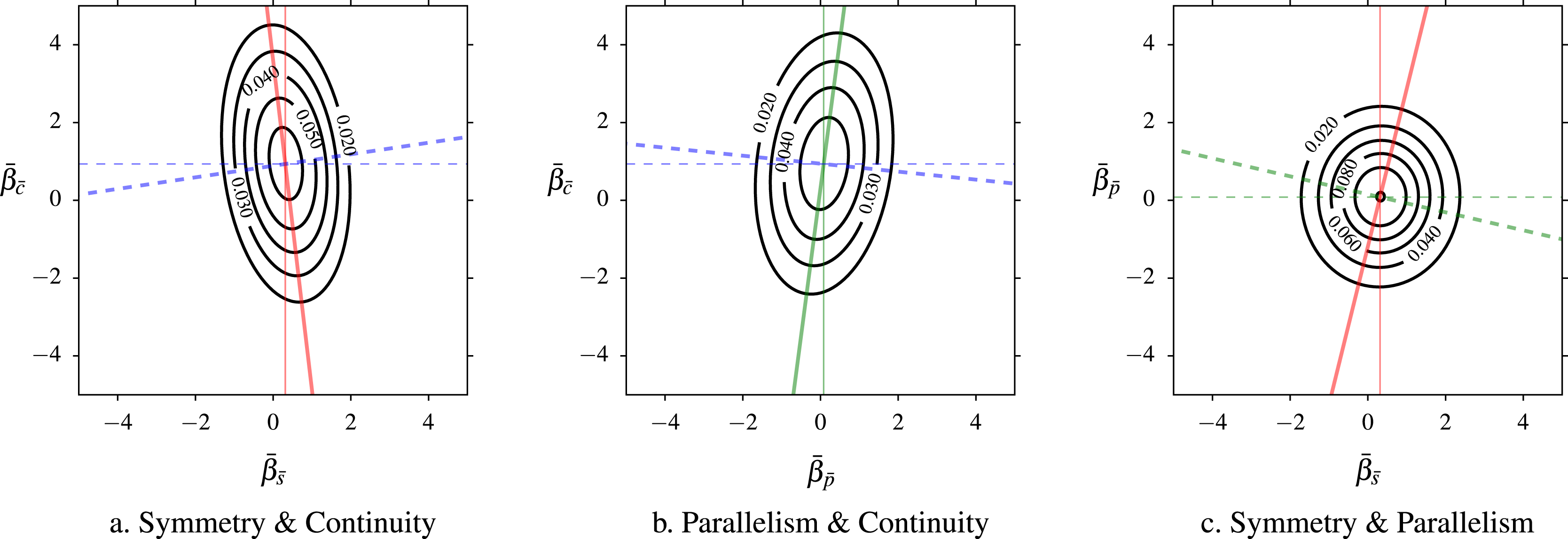
Figure 7. Multivariate joint distribution of population-level utility estimates
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
of symmetry, parallelism, and continuity for the aesthetics of a 3D bottle representation.
Table 6. Mixed logit model of aesthetic utility estimates for 3D Gestalt principles; estimation by hierarchical Bayes
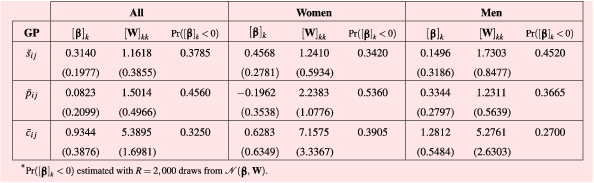
Table 7. Population-level covariance matrix
$\mathbf{W}$
Table 8. Pearson correlation coefficients in population-level covariance matrix
$\mathbf{W}$
(Table 7)
The joint distribution between the simulated part-worth utility estimates of symmetry, parallelism, and continuity (see Figure 7 and Table 7) suggests some interaction between the effects of these Gestalt principles on the aesthetic preferences for a bottle form. Although the correlation coefficient between symmetry and parallelism in Table 8 (0.0139) suggests that both principles are fairly independent of each other, both of them appear to be affected by continuity. On one hand, the resulting negative correlation between the symmetry and the continuity (
$-0.2064$
) suggests that the former has a lower positive impact on subjects’ choices in the presence of smoother bottle forms. On the other hand, parallelism gains relevance in the presence of high levels of continuity, as implied by the positive correlation between them (0.1868).
The application of the mixed logit on the choice data of women and men suggests some differences in the appreciation of parallelism for the case study. While the
$[\boldsymbol{\unicode[STIX]{x1D6FD}}]_{k}$
for continuity was the highest in every case (0.6283 for women, 1.2812 for men) and the obtained part-worth aesthetic utility estimates of symmetry were also positive (0.4568 versus 0.1496), the estimates for parallelism suggest that this principle could have had opposite effects between women and men (
$-0.1962$
versus 0.3344) (see Table 6). A Mann–Whitney–Wilcoxon (MWW) rank sum test was used to assess the third hypothesis of the study regarding the similarities between women and men in sample estimates for each Gestalt quantification. The probability values obtained from the MWW test applied between two sets of
$R=2,000$
draws each from the
$\mathscr{N}(\boldsymbol{\unicode[STIX]{x1D6FD}}_{\text{women}},\mathbf{W}_{\text{women}})$
and
$\mathscr{N}(\boldsymbol{\unicode[STIX]{x1D6FD}}_{\text{men}},\mathbf{W}_{\text{men}})$
distributions were below 0.0001. Considering a standard significance level of 5%, these results suggest that there is not enough evidence to claim that the estimates for women and men come from the same distribution and have similar medians, thus failing to accept the third hypothesis. In particular, the difference in estimates of parallelism for women and men provides an opportunity for an in-depth exploration of the effect of genre on this principle’s aesthetic utility for a larger number of subjects. Finally, Table 8 shows a high negative correlation between symmetry and continuity in men’s preferences (
$-0.5945$
), in contrast to the positive correlation between these two principles in the case of women (0.2666). This situation, combined with the positive effect of continuity on men’s aesthetic judgments and its low correlation with parallelism, could have favored an increase in the utility estimate of the latter, opposite to the results for women. Again, more samples are required to determine the trade-offs that women and men make between the three Gestalt principles.
6 Discussion
The results of the mixed logit model suggest that the first hypothesis is true regarding the relevance of the Gestalt principles of symmetry, parallelism, and continuity as predictors of subjects’ judgments about the aesthetics of a 3D bottle representation. The probability that the principles of symmetry, parallelism, and continuity have no effect on subjects’ judgments is negligible –
$\text{Pr}(\boldsymbol{\unicode[STIX]{x1D6FD}}|H_{0})<0.0001$
, which leads to rejecting the null hypothesis. Moreover, the results show that these principles might have a positive effect on aesthetic preferences for the case study, especially with continuity, the obtained mean part-worth utility estimate of which was three times higher than the one for symmetry and seven times higher than the one for parallelism (see Table 6). The skewness of the estimates of continuity in Figure 6(c) also suggest that the effect of this principle on preferences tends to be positive. Regarding the second hypothesis of independent explanatory variables, the covariance matrix from the multivariate normal distribution shows some notable interactions between continuity and the other two Gestalt principles considered. The Pearson correlation matrix derived from the covariance shows that there is not enough evidence to support the second hypothesis, and thus it is rejected.
The low mean part-worth utility estimate of parallelism conflicts with the rejection of the null hypothesis of zero effect on subjects’ aesthetic preferences. These results suggest the presence of additional factors not included in this study that are affecting the aesthetic appraisal of this principle among the participants. The part-worth utility estimates of parallelism by genre suggest that this principle could have the opposite effect on women and men, and this could explain why its overall mean part-worth utility is close to zero without rejecting the null hypothesis. Moreover, an MWW test to assess these differences fails to accept the third hypothesis that the estimates for women and men come from the same distribution and have equal medians (assuming a significance level of 5%). Further experimentation using more samples is required to determine whether subjects’ appraisals of parallelism are affected by their genre. Designers can apply this procedure to address aesthetic preferences within different social groups, and use the results for optimization of product form.
The part-worth utilities in this work for the case of a generic bottle are different from those reported by Valencia-Romero & Lugo (Reference Valencia-Romero and Lugo2016a ), who used 2D representations labeled as fragrance bottles. While the results in Valencia-Romero & Lugo’s previous work show that parallelism had a counteractive effect on subjects, this principle could have had a favorable influence on some of the participants for the case study presented herein. Moreover, the negative correlation between symmetry and continuity contrasts with the correlation obtained for the previous 2D case, for which it was found that these two principles would complement each other into a positive impression on the subjects. These differences could imply that the part-worth utilities of the Gestalt quantifications are specific to the type of representation used and to how much information about the product form is given to subjects. In this sense, there is not enough evidence to suggest that the two studies are contradictory. Further experimentation with other types of visualization and actual prototypes and external validation are necessary to check the usefulness of the quantifications in predicting aesthetic preferences and to define the limits in which they are suitable to use.
Regarding the VR experience, some subjects reported dizziness during the immersion. Designers could reduce the duration of the experiment by using a fractional factorial set of product forms instead of a full factorial, and test only main effects, to minimize the chances of subjects developing VR fatigue. Moreover, the development of a VR environment that resembles a consumer-market setting could help subjects to identify themselves with the experience and enhance the user-friendliness of virtual DCE studies. For instance, a VR environment for a DCE of fragrance bottles could consist of a luxurious boutique with each bottle on a pedestal, while the VR environment for a DCE of sedans could feature big glass walls and shiny panels typical of car dealerships or showrooms. Finally, the use of wireless equipment to give subjects the freedom to stand up and walk around the actual setting might also have a positive impact on the experience.
Designers can use the methodology presented in this paper to perform their own DCE study for the specific product that they are designing. With the modeling of aesthetics based on Gestalt principles presented in Lugo et al.’s (Reference Lugo, Schmiedeler, Batill and Carlson2016) work, designers will be able to model aesthetics based on symmetry, parallelism, and continuity principles. As described in the previous investigation, the modeling of aesthetics can be based on Gestalt principles via the aesthetic equation
$M=O/C$
, in which
$M$
is aesthetics,
$O$
is order, and
$C$
is complexity. A model for aesthetics can be constructed by taking the Gestalt quantifications as measurements of order and assuming that the complexity is constant – because all designs are based on the same parametric model. The aesthetic equation is then simplified as the
$\ell 1$
norm of the Gestalt principles – this is how aesthetics can be modeled with quantifications of Gestalt principles (e.g. symmetry, parallelism, and continuity). The current research allows the inclusion of weights for each Gestalt principle in order to take into account the difference in utility. This will enable designers to understand the trade-offs between Gestalt principles with respect to aesthetic preferences for their products. The purpose of the case study was to show designers how to apply the methodology. It was applied to a generic bottle form, and thus the results are specific to that abstraction and limited by the small sample size.
7 Conclusions
The proposed methodology approaches the introduction of aesthetic preference as a function of the Gestalt principles of symmetry, parallelism, and continuity into product development and optimization. With the use of preference elicitation methods like DCE in conjunction with VR technologies, this work shows how designers can use the 3D quantifications of these principles to study product aesthetics in more realistic and interactive settings. In addition, the results of this pilot study provide insight into subjects’ appreciation of the product form and directions for future use of VR technologies in aesthetic subject preference studies.
Acknowledgments
The authors would like to acknowledge the support of the College of Engineering of the University of Puerto Rico–Mayagüez Campus.
Open access
