Hostname: page-component-6587cd75c8-6rxlm Total loading time: 0 Render date: 2025-04-23T22:16:15.872Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeros of Rankin–Selberg L-functions in families

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  03 April 2024

Peter Humphries Open the ORCID record for Peter Humphries [Opens in a new window]  and
Jesse Thorner Open the ORCID record for Jesse Thorner [Opens in a new window]
Peter Humphries
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22904, USA URL: https://sites.google.com/view/peterhumphries/ [email protected]
Jesse Thorner
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 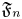$\mathfrak {F}_n$ be the set of all cuspidal automorphic representations 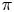$\pi$ of 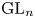$\mathrm {GL}_n$ with unitary central character over a number field 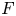$F$. We prove the first unconditional zero density estimate for the set 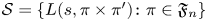$\mathcal {S}=\{L(s,\pi \times \pi ')\colon \pi \in \mathfrak {F}_n\}$ of Rankin–Selberg 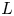$L$-functions, where 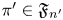$\pi '\in \mathfrak {F}_{n'}$ is fixed. We use this density estimate to establish: (i) a hybrid-aspect subconvexity bound at 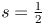$s=\frac {1}{2}$ for almost all 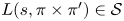$L(s,\pi \times \pi ')\in \mathcal {S}$; (ii) a strong on-average form of effective multiplicity one for almost all 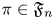$\pi \in \mathfrak {F}_n$; and (iii) a positive level of distribution for 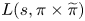$L(s,\pi \times \widetilde {\pi })$, in the sense of Bombieri–Vinogradov, for each 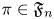$\pi \in \mathfrak {F}_n$.

Keywords

automorphic formsRankin–Selberg L-functionszero density estimatesubconvexity

MSC classification

Primary: 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F12: Automorphic forms, one variable
Secondary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 5 , May 2024 , pp. 1041 - 1072
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Banks, W. D., Twisted symmetric-square $L$-functions and the nonexistence of Siegel zeros on ${\rm GL}(3)$, Duke Math. J. 87 (1997), 343–353.CrossRefGoogle Scholar
Blomer, V., Period integrals and Rankin–Selberg $L$-functions on $GL(n)$, Geom. Funct. Anal. 22 (2012), 608–620.CrossRefGoogle Scholar
Blomer, V., Density theorems for ${\rm GL}(n)$, Invent. Math. 232 (2023), 683–711.CrossRefGoogle Scholar
Blomer, V. and Brumley, F., On the Ramanujan conjecture over number fields, Ann. of Math. (2) 174 (2011), 581–605.CrossRefGoogle Scholar
Blomer, V. and Brumley, F., Non-vanishing of $L$-functions, the Ramanujan conjecture, and families of Hecke characters, Canad. J. Math. 65 (2013), 22–51.CrossRefGoogle Scholar
Bombieri, E., On the large sieve, Mathematika 12 (1965), 201–225.CrossRefGoogle Scholar
Brumley, F., Distinguishing cusp forms on the general linear group, PhD thesis, Princeton University (ProQuest LLC, Ann Arbor, MI, 2004).Google Scholar
Brumley, F., Effective multiplicity one on ${\rm GL}_N$ and narrow zero-free regions for Rankin–Selberg $L$-functions, Amer. J. Math. 128 (2006), 1455–1474.CrossRefGoogle Scholar
Brumley, F., Second order average estimates on local data of cusp forms, Arch. Math. (Basel) 87 (2006), 19–32.CrossRefGoogle Scholar
Brumley, F. and Milićević, D., Counting cusp forms by analytic conductor, Ann. Sci. Éc. Norm. Supér. (4), to appear. Preprint (2018), arXiv:1805.00633.Google Scholar
Brumley, F., Thorner, J. and Zaman, A., Zeros of Rankin–Selberg $L$-functions at the edge of the critical strip, J. Eur. Math. Soc. (JEMS) 24 (2022), 1471–1541. With an appendix by Colin J. Bushnell and Guy Henniart.CrossRefGoogle Scholar
Bump, D., Lie groups, Graduate Texts in Mathematics, vol. 225, second edition (Springer, New York, 2013).CrossRefGoogle Scholar
Bushnell, C. J. and Henniart, G., An upper bound on conductors for pairs, J. Number Theory 65 (1997), 183–196.CrossRefGoogle Scholar
Deshouillers, J.-M. and Iwaniec, H., Kloosterman sums and Fourier coefficients of cusp forms, Invent. Math. 70 (1982/83), 219–288.CrossRefGoogle Scholar
Duke, W. and Kowalski, E., A problem of Linnik for elliptic curves and mean-value estimates for automorphic representations, Invent. Math. 139 (2000), 1–39. With an appendix by Dinakar Ramakrishnan.CrossRefGoogle Scholar
Gallagher, P. X., Bombieri's mean value theorem, Mathematika 15 (1968), 1–6.CrossRefGoogle Scholar
Gallagher, P. X., A large sieve density estimate near $\sigma =1$, Invent. Math. 11 (1970), 329–339.CrossRefGoogle Scholar
Gelbart, S. and Jacquet, H., A relation between automorphic representations of ${\rm GL}(2)$ and ${\rm GL}(3)$, Ann. Sci. Éc. Norm. Supér. (4) 11 (1978), 471–542.CrossRefGoogle Scholar
Godement, R. and Jacquet, H., Zeta functions of simple algebras, Lecture Notes in Mathematics, vol. 260 (Springer, Berlin, New York, 1972).CrossRefGoogle Scholar
Hoffstein, J. and Lockhart, P., Coefficients of Maass forms and the Siegel zero, Ann. of Math. (2) 140 (1994), 161–181. With an appendix by Dorian Goldfeld, Jeffrey Hoffstein and Daniel Lieman.CrossRefGoogle Scholar
Hoffstein, J. and Ramakrishnan, D., Siegel zeros and cusp forms, Int. Math. Res. Not. IMRN 1995 (1995), 279–308.CrossRefGoogle Scholar
Hoheisel, G., Primzahl probleme in der Analysis, S.-B. Preuss. Akad. Wiss. 8 (1930), 580–588.Google Scholar
Humphries, P., Standard zero-free regions for Rankin–Selberg $L$-functions via sieve theory, Math. Z. 292 (2019), 1105–1122. With an appendix by Farrell Brumley.CrossRefGoogle Scholar
Humphries, P. and Thorner, J., Towards a ${\rm GL}_n$ variant of the Hoheisel phenomenon, Trans. Amer. Math. Soc. 375 (2022), 1801–1824.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI. 2004).Google Scholar
Iwaniec, H. and Sarnak, P., Perspectives on the analytic theory of $L$-functions, Geom. Funct. Anal. (2000), 705–741. GAFA 2000 (Tel Aviv, 1999).Google Scholar
Jacquet, H., Piatetskii-Shapiro, I. I. and Shalika, J. A., Rankin–Selberg convolutions, Amer. J. Math. 105 (1983), 367–464.CrossRefGoogle Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I, Amer. J. Math. 103 (1981), 499–558.CrossRefGoogle Scholar
Jana, S., Applications of analytic newvectors for $\text {GL}(n)$, Math. Ann. 380 (2021), 915–952.CrossRefGoogle Scholar
Jana, S., The second moment of $\mathrm {GL}(n)\times \mathrm {GL}(n)$ Rankin–Selberg $L$-functions, Forum Math. Sigma 10 (2022), Paper No. e47.CrossRefGoogle Scholar
Jiang, Y., Lü, G., Thorner, J. and Wang, Z., A Bombieri–Vinogradov theorem for higher-rank groups, Int. Math. Res. Not. IMRN 2023 (2023), 482–535.CrossRefGoogle Scholar
Lapid, E., On the Harish–Chandra Schwartz space of $G(F)\backslash G(\mathbb {A})$, in Automorphic representations and L-functions, Tata Institute of Fundamental Research Studies in Mathematics, vol. 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 335–377. With an appendix by Farrell Brumley.Google Scholar
Li, X., Upper bounds on $L$-functions at the edge of the critical strip, Int. Math. Res. Not. IMRN 2010 (2010), 727–755.Google Scholar
Linnik, U. V., On the least prime in an arithmetic progression, Rec. Math. [Mat. Sbornik] N.S. 15 (1944), 139–178, 347–368.Google Scholar
Liu, J. and Wang, Y., A theorem on analytic strong multiplicity one, J. Number Theory 129 (2009), 1874–1882.CrossRefGoogle Scholar
Luo, W., Rudnick, Z. and Sarnak, P., On Selberg's eigenvalue conjecture, Geom. Funct. Anal. 5 (1995), 387–401.CrossRefGoogle Scholar
Luo, W., Rudnick, Z. and Sarnak, P., On the generalized Ramanujan conjecture for GL(n), in Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996), Proceedings of Symposia in Pure Mathematics, vol. 66 (American Mathematical Society, Providence, RI, 1999), 301–310.Google Scholar
Michel, P. and Venkatesh, A., The subconvexity problem for ${\rm GL}_2$, Publ. Math. Inst. Hautes Études Sci. 11 (2010), 171–271.CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Le spectre résiduel de ${\rm GL}(n)$, Ann. Sci. Éc. Norm. Supér. (4) 22 (1989), 605–674.CrossRefGoogle Scholar
Moreno, C. J., Analytic proof of the strong multiplicity one theorem, Amer. J. Math. 107 (1985), 163–206.CrossRefGoogle Scholar
Müller, W. and Speh, B., Absolute convergence of the spectral side of the Arthur trace formula for ${\rm GL}_n$, Geom. Funct. Anal. 14 (2004), 58–93. With an appendix by E. M. Lapid.Google Scholar
Murty, M. R. and Murty, V. K., A variant of the Bombieri–Vinogradov theorem, in Number theory (Montreal, Que., 1985), CMS Conference Proceedings, vol. 7 (American Mathematical Society, Providence, RI, 1987), 243–272.Google Scholar
Piatetski-Shapiro, I. I., Multiplicity one theorems, in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 209–212.Google Scholar
Ramakrishnan, D., Modularity of the Rankin–Selberg $L$-series, and multiplicity one for ${\rm SL}(2)$, Ann. of Math. (2) 152 (2000), 45–111.Google Scholar
Soundararajan, K. and Thorner, J., Weak subconvexity without a Ramanujan hypothesis, Duke Math. J. 168 (2019), 1231–1268. With an appendix by Farrell Brumley.CrossRefGoogle Scholar
Thorner, J. and Zaman, A., A unified and improved Chebotarev density theorem, Algebra Number Theory 13 (2019), 1039–1068.CrossRefGoogle Scholar
Thorner, J. and Zaman, A., An unconditional ${\rm GL}_n$ large sieve, Adv. Math. 378 (2021), 24. Paper No. 107529.CrossRefGoogle Scholar
Weiss, A., The least prime ideal, J. Reine Angew. Math. 338 (1983), 56–94.CrossRefGoogle Scholar
Wong, P.-J., Bombieri–Vinogradov theorems for modular forms and applications, Mathematika 66 (2020), 200–229.CrossRefGoogle Scholar