Article contents
Zariski closures of images of algebraic subsets under the uniformization map on finite-volume quotients of the complex unit ball
Published online by Cambridge University Press: 19 September 2019
Abstract
We prove the analogue of the Ax–Lindemann–Weierstrass theorem for not necessarily arithmetic lattices of the automorphism group of the complex unit ball 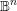 $\mathbb{B}^{n}$ using methods of several complex variables, algebraic geometry and Kähler geometry. Consider a torsion-free lattice
$\mathbb{B}^{n}$ using methods of several complex variables, algebraic geometry and Kähler geometry. Consider a torsion-free lattice 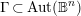 $\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$ and the associated uniformization map
$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$ and the associated uniformization map 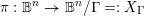 $\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow \mathbb{B}^{n}/\unicode[STIX]{x1D6E4}=:X_{\unicode[STIX]{x1D6E4}}$. Given an algebraic subset
$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow \mathbb{B}^{n}/\unicode[STIX]{x1D6E4}=:X_{\unicode[STIX]{x1D6E4}}$. Given an algebraic subset 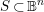 $S\,\subset \,\mathbb{B}^{n}$ and writing
$S\,\subset \,\mathbb{B}^{n}$ and writing 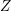 $Z$ for the Zariski closure of
$Z$ for the Zariski closure of 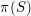 $\unicode[STIX]{x1D70B}(S)$ in
$\unicode[STIX]{x1D70B}(S)$ in 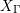 $X_{\unicode[STIX]{x1D6E4}}$ (which is equipped with a canonical quasi-projective structure), in some precise sense we realize
$X_{\unicode[STIX]{x1D6E4}}$ (which is equipped with a canonical quasi-projective structure), in some precise sense we realize 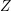 $Z$ as a variety uniruled by images of algebraic subsets under the uniformization map, and study the asymptotic geometry of an irreducible component
$Z$ as a variety uniruled by images of algebraic subsets under the uniformization map, and study the asymptotic geometry of an irreducible component 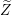 $\widetilde{Z}$ of
$\widetilde{Z}$ of 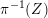 $\unicode[STIX]{x1D70B}^{-1}(Z)$ as
$\unicode[STIX]{x1D70B}^{-1}(Z)$ as 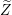 $\widetilde{Z}$ exits the boundary
$\widetilde{Z}$ exits the boundary 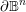 $\unicode[STIX]{x2202}\mathbb{B}^{n}$ by exploiting the strict pseudoconvexity of
$\unicode[STIX]{x2202}\mathbb{B}^{n}$ by exploiting the strict pseudoconvexity of 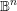 $\mathbb{B}^{n}$, culminating in the proof that
$\mathbb{B}^{n}$, culminating in the proof that 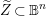 $\widetilde{Z}\,\subset \,\mathbb{B}^{n}$ is totally geodesic. Our methodology sets the stage for tackling problems in functional transcendence theory for arbitrary lattices of
$\widetilde{Z}\,\subset \,\mathbb{B}^{n}$ is totally geodesic. Our methodology sets the stage for tackling problems in functional transcendence theory for arbitrary lattices of 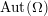 $\text{ Aut}(\unicode[STIX]{x1D6FA})$ for (possibly reducible) bounded symmetric domains
$\text{ Aut}(\unicode[STIX]{x1D6FA})$ for (possibly reducible) bounded symmetric domains 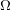 $\unicode[STIX]{x1D6FA}$.
$\unicode[STIX]{x1D6FA}$.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author 2019
Footnotes
Research partially supported by the GRF 17301518 of the HKRGC, Hong Kong.
References
- 1
- Cited by


