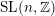Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T16:05:34.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Words have bounded width in $\operatorname{SL}(n,\mathbb{Z})$

Part of: Other groups of matrices Forms and linear algebraic groups

Published online by Cambridge University Press:  13 June 2019

Nir Avni  and
Chen Meiri
Nir Avni
Affiliation:
Department of Mathematics, Northwestern University, Evanston IL, USA email [email protected]
Chen Meiri
Affiliation:
Department of Mathematics, Technion, Haifa, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove two results about the width of words in 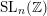$\operatorname{SL}_{n}(\mathbb{Z})$. The first is that, for every 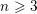$n\geqslant 3$, there is a constant 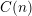$C(n)$ such that the width of any word in 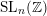$\operatorname{SL}_{n}(\mathbb{Z})$ is less than 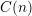$C(n)$. The second result is that, for any word 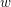$w$, if $n$ is big enough, the width of 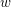$w$ in 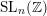$\operatorname{SL}_{n}(\mathbb{Z})$ is at most 87.

Keywords

arithmetic groupsword width

MSC classification

Primary: 20H05: Unimodular groups, congruence subgroups 11E57: Classical groups
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 7 , July 2019 , pp. 1245 - 1258
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borel, A., On free subgroups of semisimple groups , Enseign. Math. (2) 29 (1983), 151–164.Google Scholar
Dennis, R. K. and Vaserstein, L. N., On a question of M. Newman on the number of commutators , J. Algebra 118 (1988), 150–161.Google Scholar
Larsen, M. and Shalev, A., Word maps and Waring type problems , J. Amer. Math. Soc. 22 (2009), 437–466.10.1090/S0894-0347-08-00615-2Google Scholar
Liebeck, M. and Shalev, A., Diameters of finite simple groups: sharp bounds and applications , Ann. of Math. (2) 154 (2001), 383–406.Google Scholar
Lubotzky, A., Images of word maps in finite simple groups , Glasg. Math. J. 56 (2014), 465–469.Google Scholar
Mennicke, J. L., Finite factor groups of the unimodular group , Ann. of Math. (2) 81 (1965), 31–37.10.2307/1970380Google Scholar
Myasnikov, A. and Nikolaev, A., Verbal subgroups of hyperbolic groups have infinite width , J. Lond. Math. Soc. (2) 90 (2014), 573–591.Google Scholar
Morgan, A. V., Rapinchuk, A. S. and Sury, B., Bounded generation of SL2 over rings of S-integers with infinitely many units , Algebra Number Theory 12 (2018), 1949–1974.Google Scholar
Segal, D., Words: notes on verbal width in groups, London Mathematical Society Lecture Note Series, vol. 361 (Cambridge University Press, Cambridge, 2009).Google Scholar
Thom, A., Convergent sequences in discrete groups , Canad. Math. Bull. 56 (2013), 424–433.10.4153/CMB-2011-155-3Google Scholar
Tits, J., Systèmes générateurs de groupes de congruence , C. R. Acad. Sci. Paris Ser. A-B 283 (1976), A693–A695.Google Scholar
Witte Morris, D., Bounded generation of SL(n, A) (after D. Carter, G. Keller and E. Paige) , New York J. Math. 13 (2007), 383–421.Google Scholar