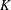Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T16:25:50.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Vanishing of negative $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic

Part of: Higher algebraic $K$-theory (Co)homology theory

Published online by Cambridge University Press:  17 July 2014

Shane Kelly
Shane Kelly*
Affiliation:
Interactive Research Center of Science, Graduate School of Science and Engineering, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro, Tokyo 152-8551, Japan email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show how a theorem of Gabber on alterations can be used to apply the work of Cisinski, Suslin, Voevodsky, and Weibel to prove that 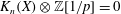$K_n(X) \otimes \mathbb{Z}[{1}/{p}]= 0$ for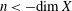$n < {-}\! \dim X$ where 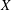$X$ is a quasi-excellent noetherian scheme, 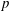$p$ is a prime that is nilpotent on 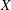$X$, and 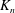$K_n$ is the 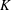$K$-theory of Bass–Thomason–Trobaugh. This gives a partial answer to a question of Weibel.

Keywords

negative K-groupsldh-topologyalterations

MSC classification

Secondary: 19D35: Negative $K$-theory, NK and Nil 14F20: Étale and other Grothendieck topologies and (co)homologies
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 8 , August 2014 , pp. 1425 - 1434
Copyright
© The Author 2014 

References

Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. I, Astérisque 314 (2007), x+466; (2008); MR 2423375 (2009h:14032).Google Scholar
Cortiñas, G., Haesemeyer, C., Schlichting, M. and Weibel, C., Cyclic homology, cdh-cohomology and negative K-theory, Ann. of Math. (2) 167 (2008), 549–573; MR 2415380 (2009c:19006).Google Scholar
Cisinski, D. C., Descente par éclatements en K-théorie invariante par homotopie, Ann. of Math. (2) 177 (2013), 425–448.Google Scholar
Friedlander, E. and Suslin, A., The spectral sequence relating algebraic K-theory to motivic cohomology, Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 773–875; MR 1949356 (2004b:19006).CrossRefGoogle Scholar
Friedlander, E. and Voevodsky, V., Bivariant cycle cohomology, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 138–187; MR 1764201.Google Scholar
Gabber, O., Finiteness theorems for étale cohomology of excellent schemes, in Conference in honor of P. Deligne on the occasion of his 61st birthday (October 2005) (IAS, Princeton, NJ, 2005).Google Scholar
Geisser, T. and Hesselholt, L., On the vanishing of negative K-groups, Math. Ann. 348 (2010), 707–736; MR 2677901 (2011j:19004).Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. 255 (1966); MR 0217086 (36 #178).Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 361 (1967); MR 0238860 (39 #220).Google Scholar
Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 2. Exposé VI: Conditions de finitude. Topos et sites fibrés. Applications aux techniques de passage á la limite, Lecture Notes in Mathematics, vol. 270 (Springer, Berlin, 1972); Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat; MR 0354653 (50 #7131).CrossRefGoogle Scholar
Haesemeyer, C., Descent properties of homotopy K-theory, Duke Math. J. 125 (2004), 589–620; MR 2166754 (2006g:19002).CrossRefGoogle Scholar
Hoyois, M., Kelly, S. and Østvær, P. A., The motivic Steenrod algebra in positive characteristic, Preprint (2013), arXiv:1305.5690.Google Scholar
Illusie, L., On gabber’s refined uniformization, http://www.math.u-psud.fr/illusie/refined_uniformization3.pdf, 2009, Notes for an exposé given at the University of Tokyo.Google Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F., Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, http://www.math.polytechnique.fr/orgogozo/travaux_de_Gabber/, 2012.Google Scholar
Johnstone, P. T., Topos theory, London Mathematical Society Monographs, vol. 10 (Academic Press [Harcourt Brace Jovanovich Publishers], London, 1977); MR 0470019 (57 #9791).Google Scholar
Kelly, S., Triangulated categories of motives in positive characteristic, PhD thesis, Université Paris 13, Australian National University (2012), arXiv:1305.5349.Google Scholar
Raynaud, M. and Gruson, L., Critères de platitude et de projectivité. Techniques de platification d’un module, Invent. Math. 13 (1971), 1–89; MR 0308104 (46 #7219).Google Scholar
Suslin, A., Higher Chow groups and etale cohomology, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 239–254; MR 1764203.Google Scholar
Suslin, A. and Voevodsky, V., Bloch-Kato conjecture and motivic cohomology with finite coefficients, in The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), NATO Science Series C: Mathematical and Physical Sciences, vol. 548 (Kluwer Academic, Dordrecht, 2000), 117–189; MR 1744945 (2001g:14031).Google Scholar
Suslin, A. and Voevodsky, V., Relative cycles and Chow sheaves, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 10–86; MR 1764199.Google Scholar
Thomason, R. W., Algebraic K-theory and étale cohomology, Ann. Sci. Éc. Norm. Supér. (4) 18 (1985), 437–552; MR 826102 (87k:14016).Google Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories, in The grothendieck festschrift, vol. III, Progress in Mathematics, vol. 88 (Birkhäuser, Boston, MA, 1990), 247–435; MR 1106918 (92f:19001).Google Scholar
Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos. Exposé II: Topologies et faisceaux, Lecture Notes in Mathematics, vol. 269 (Springer, Berlin, 1972), Séminaire de Géométrie Algébrique du Bois–Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck, et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint–Donat; MR 0354652 (50 #7130).CrossRefGoogle Scholar
Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos. Exposé III: Fonctorialité des categories des faisceaux, Lecture Notes in Mathematics, vol. 269 (Springer, Berlin, 1972), Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck, et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat; MR 0354652 (50 #7130).Google Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 188–238; MR 1764202.Google Scholar
Voevodsky, V., Homotopy theory of simplicial sheaves in completely decomposable topologies, J. Pure Appl. Algebra 214 (2010), 1384–1398; MR 2593670 (2011a:55022).Google Scholar
Voevodsky, V., Unstable motivic homotopy categories in Nisnevich and cdh-topologies, J. Pure Appl. Algebra 214 (2010), 1399–1406; MR 2593671 (2011e:14041).Google Scholar
Weibel, C., K-theory and analytic isomorphisms, Invent. Math. 61 (1980), 177–197; MR 590161 (83b:13011).CrossRefGoogle Scholar
Weibel, C., Meyer vietoris sequences and module structures on N K, in Algebraic K-theory (Evanston, 1980), Lecture Notes in Mathematics, vol. 854, eds Friedlander, E. and Stein, M. (Springer, Berlin, 1981), 466–493.CrossRefGoogle Scholar
Weibel, C., Homotopy algebraic K-theory, in Algebraic K-theory and algebraic number theory (Honolulu, HI, 1987), Contemporary Mathematics, vol. 83 (American Mathematical Society, Providence, RI, 1989), 461–488; MR 991991 (90d:18006).Google Scholar