Published online by Cambridge University Press: 27 September 2010
We show that there is an essentially unique S-algebra structure on the Morava K-theory spectrum K(n), while K(n) has uncountably many MU or 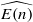 -algebra structures. Here
-algebra structures. Here 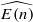 is the K(n)-localized Johnson–Wilson spectrum. To prove this we set up a spectral sequence computing the homotopy groups of the moduli space of A∞ structures on a spectrum, and use the theory of S-algebra k-invariants for connectiveS-algebras found in the work of Dugger and Shipley [Postnikov extensions of ring spectra, Algebr. Geom. Topol. 6 (2006), 1785–1829 (electronic)] to show that all the uniqueness obstructions are hit by differentials.
is the K(n)-localized Johnson–Wilson spectrum. To prove this we set up a spectral sequence computing the homotopy groups of the moduli space of A∞ structures on a spectrum, and use the theory of S-algebra k-invariants for connectiveS-algebras found in the work of Dugger and Shipley [Postnikov extensions of ring spectra, Algebr. Geom. Topol. 6 (2006), 1785–1829 (electronic)] to show that all the uniqueness obstructions are hit by differentials.