Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bourgain, Jean
and
Kontorovich, Alex
2011.
On Zarembaʼs conjecture.
Comptes Rendus. Mathématique,
Vol. 349,
Issue. 9-10,
p.
493.
Kontorovich, Alex
2014.
Levels of Distribution and the Affine Sieve.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 23,
Issue. 5,
p.
933.
Bourgain, Jean
and
Kontorovich, Alex
2014.
On Zaremba's conjecture.
Annals of Mathematics,
Vol. 180,
Issue. 1,
p.
137.
AKA, MENNY
and
EINSIEDLER, MANFRED
2016.
Duke’s theorem for subcollections.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 2,
p.
335.
Aka, Menny
and
Shapira, Uri
2018.
On the evolution of continued fractions in a fixed quadratic field.
Journal d'Analyse Mathématique,
Vol. 134,
Issue. 1,
p.
335.
Morier-Genoud, Sophie
and
Ovsienko, Valentin
2019.
Farey Boat: Continued Fractions and Triangulations, Modular Group and Polygon Dissections.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 121,
Issue. 2,
p.
91.
Kontorovich, Alex
2022.
Analysis at Large.
p.
253.


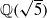 contains the infinite sequence of uniformly bounded continued fractions
contains the infinite sequence of uniformly bounded continued fractions 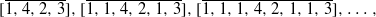 and similar patterns can be found in
and similar patterns can be found in 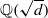 for any
for any 