Let k be a non-Archimedean field, let X be a k-affinoid space and let f1,…,fn, with 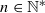, be analytic functions over X. If X is irreducible, we prove that the analytic domain 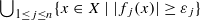is still irreducible, provided that 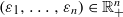is small enough. Then, for a general X, we precisely describe how the geometric connected components of the spaces 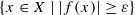behave with regards to ε. Finally, we obtain a result concerning privileged neighbourhoods and adapt a theorem from complex analytic geometry about Noetherianity for germs of analytic functions.