Published online by Cambridge University Press: 13 May 2024
Let 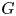 $G$ be a reductive group, and let
$G$ be a reductive group, and let 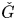 $\check {G}$ be its Langlands dual group. Arkhipov and Bezrukavnikov proved that the Whittaker category on the affine flags
$\check {G}$ be its Langlands dual group. Arkhipov and Bezrukavnikov proved that the Whittaker category on the affine flags 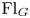 ${\operatorname {Fl}}_G$ is equivalent to the category of
${\operatorname {Fl}}_G$ is equivalent to the category of 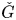 $\check {G}$-equivariant quasi-coherent sheaves on the Springer resolution of the nilpotent cone. This paper proves this theorem in the quantum case. We show that the twisted Whittaker category on
$\check {G}$-equivariant quasi-coherent sheaves on the Springer resolution of the nilpotent cone. This paper proves this theorem in the quantum case. We show that the twisted Whittaker category on 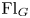 ${\operatorname {Fl}}_G$ and the category of representations of the mixed quantum group are equivalent. In particular, we prove that the quantum category
${\operatorname {Fl}}_G$ and the category of representations of the mixed quantum group are equivalent. In particular, we prove that the quantum category 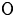 $\mathsf {O}$ is equivalent to the twisted Whittaker category on
$\mathsf {O}$ is equivalent to the twisted Whittaker category on 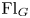 ${\operatorname {Fl}}_G$ in the generic case. The strong version of our main theorem claims a motivic equivalence between the Whittaker category on
${\operatorname {Fl}}_G$ in the generic case. The strong version of our main theorem claims a motivic equivalence between the Whittaker category on 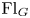 ${\operatorname {Fl}}_G$ and a factorization module category, which holds in the de Rham setting, the Betti setting, and the
${\operatorname {Fl}}_G$ and a factorization module category, which holds in the de Rham setting, the Betti setting, and the 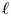 $\ell$-adic setting.
$\ell$-adic setting.