Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T13:31:28.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Toric degenerations of cluster varieties and cluster duality

Part of: Arithmetic rings and other special rings Families, fibrations Special varieties

Published online by Cambridge University Press:  07 December 2020

Lara Bossinger ,
Bosco Frías-Medina ,
Timothy Magee  and
Alfredo Nájera Chávez
Lara Bossinger
Affiliation:
Instituto de Matemáticas UNAM Unidad Oaxaca, León 2, altos, Oaxaca de Juárez, Centro Histórico, 68000Oaxaca, [email protected]
Bosco Frías-Medina
Affiliation:
Centro de Ciencias Matemáticas UNAM Campus Morelia, Antigua Carretera a Pátzcuaro 8701, Col. Ex Hacienda San José de la Huerta, 58089Michoacán, [email protected]
Timothy Magee
Affiliation:
Department of Mathematics, Faculty of Natural & Mathematical Sciences, King's College London, Strand, London WC2R 2LS, UK [email protected]
Alfredo Nájera Chávez
Affiliation:
CONACYT-Instituto de Matemáticas UNAM Unidad Oaxaca, León 2, altos, Oaxaca de Juárez, Centro Histórico, 68000Oaxaca, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of a 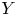$Y$-pattern with coefficients and its geometric counterpart: an 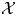$\mathcal {X}$-cluster variety with coefficients. We use these constructions to build a flat degeneration of every skew-symmetrizable specially completed 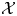$\mathcal {X}$-cluster variety 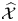$\widehat {\mathcal {X} }$ to the toric variety associated to its g-fan. Moreover, we show that the fibers of this family are stratified in a natural way, with strata the specially completed 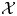$\mathcal {X}$-varieties encoded by 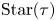$\operatorname {Star}(\tau )$ for each cone 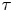$\tau$ of the 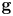$\mathbf {g}$-fan. These strata degenerate to the associated toric strata of the central fiber. We further show that the family is cluster dual to 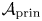$\mathcal {A}_{\mathrm {prin}}$ of Gross, Hacking, Keel and Kontsevich [Canonical bases for cluster algebras, J. Amer. Math. Soc. 31 (2018), 497–608], and the fibers cluster dual to 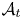$\mathcal {A} _t$. Finally, we give two applications. First, we use our construction to identify the toric degeneration of Grassmannians from Rietsch and Williams [Newton-Okounkov bodies, cluster duality, and mirror symmetry for Grassmannians, Duke Math. J. 168 (2019), 3437–3527] with the Gross–Hacking–Keel–Kontsevich degeneration in the case of 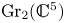$\operatorname {Gr}_2(\mathbb {C} ^{5})$. Next, we use it to link cluster duality to Batyrev–Borisov duality of Gorenstein toric Fanos in the context of mirror symmetry.

Keywords

cluster algebrascluster varietiestoric degenerations

MSC classification

Primary: 13F60: Cluster algebras
Secondary: 14M25: Toric varieties, Newton polyhedra 14D06: Fibrations, degenerations
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 10 , October 2020 , pp. 2149 - 2206
Check for updates
Copyright
© The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by CONACYT grant CB2016 no. 284621. The first author was partially supported by the Max Planck Institute of Mathematics in the Sciences, Leipzig and the ‘Programa de Becas Posdoctorales en la UNAM 2018’ Instituto de Matemáticas, UNAM. The second and third authors acknowledge the support of Fondo Institucional de Fomento Regional para el Desarrollo Científico, Tecnológico y de Innovación, FORDECYT 265667. The second author was additionally supported by ‘Programa de Becas Posdoctorales 2019’, DGAPA, UNAM during the revisions of this article. The third author was additionally partially supported by EPSRC grant EP/P021913/1 during revisions of this article.

References

Allegretti, D. G. L. and Bridgeland, T., The monodromy of meromorphic projective structures, Trans. Amer. Math. Soc. 373 (2020), 6321–6367.CrossRefGoogle Scholar
Anderson, D., Okounkov bodies and toric degenerations, Math. Ann. 356 (2013), 1183–1202.CrossRefGoogle Scholar
Batyrev, V. V., Dual polyhedra and mirror symmetry for Calabi–Yau hypersurfaces in toric varieties, J. Algebraic Geom. 3 (1994), 493–535.Google Scholar
Bossinger, L. and Fourier, G., String cone and superpotential combinatorics for flag and Schubert varieties in type A, J. Combin. Theory Ser. A 167 (2019), 213–256.CrossRefGoogle Scholar
Berenstein, A., Fomin, S. and Zelevinsky, A., Parametrizations of canonical bases and totally positive matrices, Adv. Math. 122 (1996), 49–149.CrossRefGoogle Scholar
Bridgeland, T., Scattering diagrams, Hall algebras and stability conditions, Algebr. Geom. 4 (2017), 523–561.CrossRefGoogle Scholar
Cao, P. and Li, F., The enough g-pairs property and denominator vectors of cluster algebras, Math. Ann. 377 (2020), 1547–1572.CrossRefGoogle Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties, Graduate Studies in Mathematics, vol. 124 (American Mathematical Society, Providence, RI, 2011).CrossRefGoogle Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations II: applications to cluster algebras, J. Amer. Math. Soc. 23 (2010), 749–790.CrossRefGoogle Scholar
Dolgachev, I. V., Classical algebraic geometry: a modern view (Cambridge University Press, Cambridge, 2012).CrossRefGoogle Scholar
Fang, X., Fourier, G. and Littelmann, P., On toric degenerations of flag varieties, in Representation Theory - Current Trends and Perspectives, eds H. Krause, P. Littlemann, G. Malle, K.-H. Neeb and C. Schweigert, EMS Series of Congress Reports (European Mathematical Society, Zürich, Switzerland, 2016), 187–232.CrossRefGoogle Scholar
Fock, V. V. and Chekhov, L. O., Quantum Teichmüller spaces, Teoret. Mat. Fiz. 120 (1999), 511–528.Google Scholar
Fock, V. and Goncharov, A., Moduli spaces of local systems and higher Teichmüller theory, Publ. Math. Inst. Hautes Études Sci. 103 (2006), 1–211.CrossRefGoogle Scholar
Fock, V. V. and Goncharov, A. B., Dual Teichmüller and lamination spaces, in Handbook of Teichmüller Theory, vol. 1, ed. A. Papadopoulos (European Mathematical Society, Zürich, 2007), 647–684.CrossRefGoogle Scholar
Fock, V. V. and Goncharov, A. B., Cluster ensembles, quantization and the dilogarithm, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 865–930.CrossRefGoogle Scholar
Fock, V. V. and Goncharov, A. B., The quantum dilogarithm and representations of quantum cluster varieties, Invent. Math. 175 (2009), 223–286.CrossRefGoogle Scholar
Fock, V. V. and Goncharov, A. B., Cluster Poisson varieties at infinity, Selecta Math. (N.S.) 22 (2016), 2569–2589.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations, J. Amer. Math. Soc. 15 (2002), 497–529.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. II. Finite type classification, Invent. Math. 154 (2003), 63–121.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Y-systems and generalized associahedra, Ann. Math. 158 (2003), 977–1018.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. IV. Coefficients, Compos. Math. 143 (2007), 112–164.CrossRefGoogle Scholar
Fu, C., $c$-vectors via $\tau$-tilting theory, J. Algebra 473 (2017), 194–220.CrossRefGoogle Scholar
Fu, C. and Keller, B., On cluster algebras with coefficients and 2-Calabi-Yau categories, Trans. Amer. Math. Soc. 362 (2010), 859–895.CrossRefGoogle Scholar
Fulton, W., Introduction to toric varieties, Annals of Mathematics Studies, vol. 131 (Princeton University Press, Princeton, NJ, 1993). The William H. Roever Lectures in Geometry.CrossRefGoogle Scholar
Genz, V., Koshevoy, G. and Schumann, B., Combinatorics of canonical bases revisited: Type A, Preprint (2016), arXiv:1611.03465.Google Scholar
Genz, V., Koshevoy, G. and Schumann, B., Polyhedral parametrizations of canonical bases & cluster duality, Adv. Math. 369 (2020), 107178.CrossRefGoogle Scholar
Gross, M., Hacking, P. and Keel, S., Birational geometry of cluster algebras, Algebr. Geom. 2 (2015), 137–175.CrossRefGoogle Scholar
Gross, M., Hacking, P., Keel, S. and Kontsevich, M., Canonical bases for cluster algebras, J. Amer. Math. Soc. 31 (2018), 497–608.CrossRefGoogle Scholar
Gross, M. and Siebert, B., From real affine geometry to complex geometry, Ann. Math. (2) 174 (2011), 1301–1428.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. I. Le langage des schémas, Inst. Hautes Études Sci. Publ. Math. 4 (1960), 228.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Troisième partie, Publ. Math. IHÉS 28 (1966).CrossRefGoogle Scholar
Kaveh, K., Crystal bases and Newton–Okounkov bodies, Duke Math. J. 164 (2015), 2461–2506.CrossRefGoogle Scholar
Kaveh, K. and Khovanskii, A. G., Newton-Okounkov bodies, semigroups of integral points, graded algebras and intersection theory, Ann. Math. (2) 176 (2012), 925–978.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Wall-crossing structures in Donaldson-Thomas invariants, integrable systems and mirror symmetry, in Homological mirror symmetry and tropical geometry, Lecture Notes of the Unione Matematica Italiana, vol. 15 (Springer, Cham, 2014), 197–308.CrossRefGoogle Scholar
Lazarsfeld, R. and Mustaţă, M., Convex bodies associated to linear series, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 783–835.CrossRefGoogle Scholar
Le, I., Higher laminations and affine buildings, Geom. Topol. 20 (2016), 1673–1735.CrossRefGoogle Scholar
Li, S. and Rupel, D., Symplectic groupoids for cluster manifolds, J. Geom. Phys. 154 (2020), 103688.CrossRefGoogle Scholar
Magee, T., Littlewood-Richardson coefficients via mirror symmetry for cluster varieties, Proc. Lond. Math. Soc. (3) 121 (2020), 463–512.CrossRefGoogle Scholar
Marsh, R. J. and Rietsch, K., The $B$-model connection and mirror symmetry for Grassmannians, Adv. Math. 366 (2020), 107027.CrossRefGoogle Scholar
Nájera Chávez, A., c-vectors and dimension vectors for cluster-finite quivers, Bull. Lond. Math. Soc. 45 (2013), 1259–1266.CrossRefGoogle Scholar
Nájera Chávez, A., On the c-vectors of an acyclic cluster algebra, Int. Math. Res. Not. IMRN 2015 (2015), 1590–1600.CrossRefGoogle Scholar
Nakanishi, T., Synchronicity phenomenon in cluster patterns, Preprint (2019), arXiv:1906.12036v4.CrossRefGoogle Scholar
Nakanishi, T. and Stella, S., Diagrammatic description of c-vectors and d-vectors of cluster algebras of finite type, Electron. J. Combin. 21 (2014), Paper 1.3.CrossRefGoogle Scholar
Nakanishi, T. and Zelevinsky, A., On tropical dualities in cluster algebras, in Algebraic groups and quantum groups, Contemporary Mathematics, vol. 565 (American Mathematical Society, Providence, RI, 2012), 217–226.CrossRefGoogle Scholar
Oda, T., Convex bodies and algebraic geometry, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 15 (Springer, Berlin, 1988). An introduction to the theory of toric varieties, Translated from the Japanese.Google Scholar
Okounkov, A., Multiplicities and Newton polytopes, in Kirillov's seminar on representation theory, American Mathematical Society Translations: Series 2, vol. 181 (American Mathematical Society, Providence, RI, 1998), 231–244.CrossRefGoogle Scholar
Postnikov, A., Total positivity, Grassmannians, and networks, Preprint (2006), arXiv:math/0609764.Google Scholar
Reading, N., Scattering fans, Preprint (2017), arXiv:1712.06968v2.Google Scholar
Reading, N., A combinatorial approach to scattering diagrams, Algebr. Comb. 3 (2020), 603–636.Google Scholar
Rietsch, K. and Williams, L., Newton-Okounkov bodies, cluster duality, and mirror symmetry for Grassmannians, Duke Math. J. 168 (2019), 3437–3527.CrossRefGoogle Scholar
Sherman-Bennett, M., Combinatorics of $\mathcal {X}$-variables in finite type cluster algebras, J. Combin. Theory Ser. A 165 (2019), 273–298.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project, 2018, https://stacks.math.columbia.edu.Google Scholar