Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T01:31:28.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological Fukaya category and mirror symmetry for punctured surfaces

Part of: Abelian categories Symplectic geometry, contact geometry

Published online by Cambridge University Press:  14 March 2019

James Pascaleff  and
Nicolò Sibilla
James Pascaleff
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1406 West Green Street, Urbana, IL 61801, USA email [email protected]
Nicolò Sibilla
Affiliation:
Max Planck Institute for Mathematics, Bonn, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we establish a version of homological mirror symmetry for punctured Riemann surfaces. Following a proposal of Kontsevich we model A-branes on a punctured surface 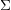$\unicode[STIX]{x1D6F4}$ via the topological Fukaya category. We prove that the topological Fukaya category of 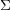$\unicode[STIX]{x1D6F4}$ is equivalent to the category of matrix factorizations of a certain mirror LG model 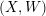$(X,W)$. Along the way we establish new gluing results for the topological Fukaya category of punctured surfaces which are of independent interest.

Keywords

Fukaya category of surfacesmirror symmetrytoric Calabi–Yau threefold

MSC classification

Primary: 18E30: Derived categories, triangulated categories 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 3 , March 2019 , pp. 599 - 644
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: School of Mathematics, Statistics and Actuarial Science (SMSAS), University of Kent, Sibson Building, Parkwood Road, Canterbury, CT2 7FS, UK email [email protected]

References

Abouzaid, M., Auroux, D., Efimov, A. I., Katzarkov, L. and Orlov, D., Homological mirror symmetry for punctured spheres , J. Amer. Math. Soc. 26 (2013), 1051–1083.Google Scholar
Ben-Zvi, D., Francis, J. and Nadler, D., Integral transforms and Drinfeld centers in derived algebraic geometry , J. Amer. Math. Soc. 23 (2010), 909–966.Google Scholar
Bocklandt, R., Noncommutative mirror symmetry for punctured surfaces , Trans. Amer. Math. Soc. 368 (2016), 429–469; with an appendix by Mohammed Abouzaid.Google Scholar
Bouchard, V. and Sułkowski, P., Topological recursion and mirror curves , Adv. Theor. Math. Phys. 16 (2012), 1443–1483.Google Scholar
Brodsky, S., Joswig, M., Morrison, R. and Sturmfels, B., Moduli of tropical plane curves , Res. Math. Sci. 2 (2015), 1–31.Google Scholar
Cohn, L., Differential graded categories are k-linear stable infinity categories, Preprint (2013), arXiv:1308.2587.Google Scholar
Connes, A., Noncommutative geometry (Academic Press, San Diego, New York, London, 1994).Google Scholar
Dyckerhoff, T., A1 -homotopy invariants of topological Fukaya categories of surfaces , Compositio Math. 153 (2017), 1673–1705.10.1112/S0010437X17007205Google Scholar
Dyckerhoff, T. and Kapranov, M., Triangulated surfaces in triangulated categories , J. Eur. Math. Soc. 20 (2018), 1473–1524.Google Scholar
Drinfeld, V. and Gaitsgory, D., Compact generation of the category of D-modules on the stack of  G-bundles on a curve , Camb. J. Math. 3 (2015), 19–125.Google Scholar
Eisenbud, D., Homological algebra on a complete intersection, with an application to group representations , Trans. Amer. Math. Soc. 260 (1980), 35–64.Google Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry: Volume I: correspondences and duality, Mathematical Surveys and Monographs, vol. 221 (American Mathematical Society, Providence, RI, 2017).Google Scholar
Genovese, F., Adjunctions of quasi-functors between dg-categories , Appl. Categ. Structures 25 (2017), 625–657.10.1007/s10485-016-9470-yGoogle Scholar
Gross, M., Katzarkov, L. and Ruddat, H., Towards mirror symmetry for varieties of general type , Adv. Math. 308 (2017), 208–275.Google Scholar
Haiden, F., Katzarkov, L. and Kontsevich, M., Flat surfaces and stability structures , Publ. Math. Inst. Hautes Études Sci. 126 (2017), 247–318.Google Scholar
Haugseng, R., Rectification of enriched ∞-categories , Algebr. Geom. Topol. 15 (2015), 1931–1982.Google Scholar
Hori, K. and Vafa, C., Mirror symmetry, Preprint (2015), arXiv:hep-th/0002222.Google Scholar
Kontsevich, M., Symplectic geometry of homological algebra, Lecture at Mathematische Arbeitstagung (2009); notes at https://www.ihes.fr/maxim/TEXTS/Symplectic_AT2009.pdf.Google Scholar
Kuwagaki, T., The nonequivariant coherent-constructible correspondence for toric stacks, Preprint (2016), arXiv:1610.03214.Google Scholar
Lee, H., Homological mirror symmetry for Riemann surfaces from pair-of-pants decompositions, Doctoral Dissertation, University of California at Berkeley (2015), http://escholarship.org/uc/item/74b3j149#page-1 and arXiv:1608.04473.Google Scholar
Lekili, Y. and Polishchuck, A., Auslander orders over nodal stacky curves and partially wrapped Fukaya categories , J. Topol. 11 (2018), 615–644.Google Scholar
Lin, K. and Pomerleano, D., Global matrix factorizations , Math. Res. Lett. 20 (2013), 91–106.Google Scholar
Lunts, V. and Schnürer, O., Matrix factorizations and semi-orthogonal decompositions for blowing-ups , J. Noncommut. Geom. 10 (2016), 907–980.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies 170 (Princeton University Press, 2009).Google Scholar
Mulase, M. and Penkava, M., Ribbon graphs, quadratic differentials on Riemann surfaces, and algebraic curves defined over ̄ , Asian J. Math. 2 (1998), 875–920.Google Scholar
Nadler, D., Microlocal branes are constructible sheaves , Selecta Math. 15 (2009), 563–619.Google Scholar
Nadler, D., Cyclic symmetry of A n quiver representations , Adv. Math. 269 (2015), 346–363.Google Scholar
Nadler, D., Mirror symmetry for the Landau–Ginzburg A-model $M=\mathbb{C}^{n}$ , $W=z_{1}\ldots z_{n}$ , Preprint (2016), arXiv:1601.02977.Google Scholar
Nadler, D., Wrapped microlocal sheaves on pairs of pants, Preprint (2016), arXiv:1604.00114.Google Scholar
Nadler, D., A combinatorial calculation of the Landau–Ginzburg model M = 3 , W = z 1 z 2 z 3 , Selecta Math. 23 (2017), 519–532.Google Scholar
Nadler, D., Arboreal singularities , Geom. Topol. 21 (2017), 1231–1274.Google Scholar
Nadler, D. and Zaslow, E., Constructible sheaves and the Fukaya category , J. Amer. Math. Soc. 22 (2009), 233–286.Google Scholar
Orlov, D., Triangulated categories of singularities and D-branes in Landau–Ginzburg models , Proc. Steklov Inst. Math. 246 (2004), 227–248.Google Scholar
Orlov, D., Matrix factorizations for non affine LG models , Math. Ann. 353 (2012), 95–108.Google Scholar
Preygel, A., Thom-Sebastiani and duality for matrix factorizations, and results on the higher structures of the Hochschild invariants, PhD thesis, Massachusetts Institute of Technology (ProQuest LLC, Ann Arbor, MI, 2012). Preprint (2011), arXiv:1101.5834.Google Scholar
Ruddat, H., Sibilla, N., Treumann, D. and Zaslow, E., Skeleta of affine hypersurfaces , Geom. Topol. 18 (2014), 1343–1395.Google Scholar
Sheridan, N., On the homological mirror symmetry conjecture for pairs of pants , J. Differential Geom. 89 (2011), 271–367.Google Scholar
Sibilla, N., Treumann, D. and Zaslow, E., Ribbon graphs and mirror symmetry , Selecta Math. 20 (2014), 979–1002.Google Scholar
Sylvan, Z., On partially wrapped Fukaya categories, PhD thesis, University of California, Berkeley (ProQuest LLC, Ann Arbor, MI, 2015). Preprint (2016), arXiv:1604.02540.Google Scholar
Tabuada, G., Une structure de catégorie de modeles de Quillen sur la catégorie des dg-catégories , C. R. Math. Acad. Sci. Paris 340 (2005), 15–19.Google Scholar
Tamarkin, D., Microlocal category, Preprint (2015), arXiv:1511.08961.Google Scholar
Toën, B., The homotopy theory of dg-categories and derived Morita theory , Invent. math. 167 (2007), 615–667.Google Scholar
Tsygan, B., A microlocal category associated to a symplectic manifold, Preprint (2015), arXiv:1512.02747.Google Scholar