Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-12T08:56:37.241Z Has data issue: false hasContentIssue false
  • English
  • Français

The test function conjecture for local models of Weil-restricted groups

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  06 July 2020

Thomas J. Haines  and
Timo Richarz
Thomas J. Haines
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742-4015, USA email [email protected]
Timo Richarz
Affiliation:
Fachbereich Mathematik, TU Darmstadt, Schlossgartenstrasse 7, 64289Darmstadt, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

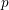We prove the test function conjecture of Kottwitz and the first named author for local models of Shimura varieties with parahoric level structure attached to Weil-restricted groups, as defined by B. Levin. Our result covers the (modified) local models attached to all connected reductive groups over $p$-adic local fields with 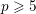$p\geqslant 5$. In addition, we give a self-contained study of relative affine Grassmannians and loop groups formed using general relative effective Cartier divisors in a relative curve over an arbitrary Noetherian affine scheme.

Keywords

Shimura varietieslocal modelsnearby cycles

MSC classification

Primary: 14G35: Modular and Shimura varieties 11G18: Arithmetic aspects of modular and Shimura varieties 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture)
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 7 , July 2020 , pp. 1348 - 1404
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of T.J.H. partially supported by NSF DMS-1406787 and by Simons Fellowship 399424, and research of T.R. funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) 394587809.

References

Alper, J., Adequate moduli spaces and geometrically reductive group schemes, Algebr. Geom. 1 (2014), 489–531.10.14231/AG-2014-022CrossRefGoogle Scholar
Arkhipov, S. and Bezrukavnikov, R., Perverse sheaves on affine flags and Langlands dual group, Israel J. Math. 170 (2009), 135–183.CrossRefGoogle Scholar
Beauville, A. and Laszlo, Y., Un lemme de descente, C. R. Acad. Sci. Paris Sér. I Math. 320 (1995), 335–340.Google Scholar
Beilinson, A. and Drinfeld, V., Quantization of Hitchin’s integrable system and Hecke eigensheaves, Preprint (1999), http://www.math.utexas.edu/users/benzvi/Langlands.html.Google Scholar
Bhatt, B., Algebraization and Tannaka duality, Camb. J. Math. 4 (2016), 403–461.CrossRefGoogle Scholar
Borel, A., Automorphic L-functions, in Automorphic forms, representations and L-functions, Part 2, Proceedings of Symposia in Pure Mathematics, vol. 33 (American Mathematical Society, Providence, RI, 1979), 27–61.CrossRefGoogle Scholar
Borovoi, M., Abelian Galois cohomology of reductive algebraic groups, Mem. Amer. Math. Soc. 626 (1998), 4206.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local II. Schémas en groupes. Existence d’une donnée radicielle valuée, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376.Google Scholar
Conrad, B., Reductive group schemes, in Autour des schémas en groupes, Group schemes, A celebration of SGA3, Vol. I, Panoramas et synthèses, vol. 42–43 (Société Mathématique de France, Paris, 2014).Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive groups (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Drinfeld, V. G., On algebraic spaces with an action of $\mathbb{G}_{m}$, Preprint (2013), arXiv:1308.2604.Google Scholar
Fantechi, B. et al. , Fundamental algebraic geometry: Grothendieck’s FGA explained, Mathematical Surveys and Monographs, vol. 123 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Fedorov, R., On the Grothendieck–Serre conjecture on principal bundles in mixed characteristic, Preprint (2016), arXiv:1501.04224.Google Scholar
Fedorov, R. and Panin, I., A proof of the Grothendieck–Serre conjecture on principal bundles over regular local rings containing infinite fields, Publ. Math. Inst. Hautes Études Sci. 122 (2015), 169–193.CrossRefGoogle Scholar
Feng, T., Nearby cycles of parahoric shtukas, and a fundamental lemma for base change, Selecta Math. (N.S.) 26 (2020), Paper No. 21.CrossRefGoogle Scholar
Gaitsgory, D., On deJong’s conjecture, Israel J. Math. 157 (2007), 155–191.CrossRefGoogle Scholar
Ginzburg, V., Perverse sheaves on a loop group and Langlands’ duality, Preprint (1995),arXiv:alg-geom/9511007.Google Scholar
Görtz, U. and Wedhorn, T., Algebraic geometry I: Schemes with examples and exercises, Advanced Lectures in Mathematics (Vieweg+Tuebner Verlag, Wiesbaden, 2010).CrossRefGoogle Scholar
Haines, T., The stable Bernstein center and test functions for Shimura varieties, in Automorphic forms and Galois representations, Vol. 2, London Mathematical Society Lecture Notes, Series, vol. 415, eds Diamond, F., Kassaei, P. and Kim, M. (Cambridge University Press, Cambridge, 2014), 118–186.CrossRefGoogle Scholar
Haines, T., On Satake parameters for representations with parahoric fixed vectors, Int. Math. Res. Not. IMRN 2015 (2015), 10367–10398.CrossRefGoogle Scholar
Haines, T., Correction to ‘On Satake parameters for representations with parahoric fixed vectors’, Int. Math. Res. Not. IMRN 2017 (2017), 4160–4170.CrossRefGoogle Scholar
Haines, T., Dualities for root systems with automorphisms and applications to non-split groups, Represent. Theory 22 (2018), 1–26.CrossRefGoogle Scholar
Haines, T. and Rapoport, M., On parahoric subgroups, Adv. Math. 219 (2008), 188–198.CrossRefGoogle Scholar
Haines, T. and Rapoport, M., Shimura varieties with 𝛤1(p)-level via Hecke algebra isomorphisms: the Drinfeld case, Ann. Sci. Éc. Norm. Supér. (4) 45 (2012), 719–785.CrossRefGoogle Scholar
Haines, T. and Richarz, T., The test function conjecture for parahoric local models, J. Amer. Math. Soc., to appear. Preprint (2018), arXiv:1801.07094.Google Scholar
Haines, T. and Richarz, T., Normality and Cohen–Macaulayness of parahoric local models, Preprint (2019), arXiv:1903.10585.Google Scholar
He, X., Pappas, G. and Rapoport, M., Good and semi-stable reductions of Shimura varieties, Preprint (2018), arXiv:1804.09615.Google Scholar
Heinloth, J., Uniformization of 𝓖-bundles, Math. Ann. 347 (2010), 499–528.CrossRefGoogle Scholar
Heinloth, J., Hilbert–Mumford stability on algebraic stacks and applications to 𝓖-bundles on curves, Épijournal de Géométrie Algébrique 1 (2018), article No. 11.Google Scholar
Hesselink, W. H., Concentration under actions of algebraic groups, in Séminaire d’Algèbre Paul Dubreil et Marie-Paule Malliavin (Springer, Berlin, 1981), 55–89.CrossRefGoogle Scholar
Illusie, L., Autour du théorème de monodromie locale, in Périodes p-adiques – Séminaire de Bures, 1988, Astérisque, vol. 223 (Société Mathématique de France, Paris, 1994), 9–57.Google Scholar
Kisin, M. and Pappas, G., Integral models of Shimura varieties with parahoric level structure, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 121–218.CrossRefGoogle Scholar
Kottwitz, R., Isocrystals with additional structures II, Compos. Math. 109 (1997), 255–339.CrossRefGoogle Scholar
Levin, B., $G$-valued flat deformations and local models, PhD thesis, Stanford University (2013).Google Scholar
Levin, B., Local models for Weil-restricted groups, Compos. Math. 152 (2016), 2563–2601.CrossRefGoogle Scholar
Lusztig, G., Singularities, character formulas, and a q-analogue of weight multiplicities, in Analysis and Topology on Singular Spaces, II, III, Astérisque, vol. 101–102 (Société Mathématique de France, Paris, 1983), 208–229.Google Scholar
Margaux, B., Smoothness of limit functors, Proc. Indian Acad. Sci. Math. Sci. 125 (2015), 161–165.CrossRefGoogle Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143.CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their affine flag varieties, Adv. Math. 219 (2008), 118–198.CrossRefGoogle Scholar
Pappas, G. and Zhu, X., Local models of Shimura varieties and a conjecture of Kottwitz, Invent. Math. 194 (2013), 147–254.CrossRefGoogle Scholar
Reich, R., Twisted geometric Satake equivalence via gerbes on the factorizable Grassmannian, Represent. Theory 16 (2012), 345–449.CrossRefGoogle Scholar
Richarz, T., A new approach to the geometric Satake equivalence, Doc. Math. 19 (2014), 209–246.Google Scholar
Richarz, T., On the Iwahori–Weyl group, Bull. Soc. Math. France 144 (2016), 117–124; fascicule 1.CrossRefGoogle Scholar
Richarz, T., Affine Grassmannians and Geometric Satake equivalences, Int. Math. Res. Not. IMRN 2016 (2016), 3717–3767.CrossRefGoogle Scholar
Richarz, T., Spaces with 𝔾m-action, hyperbolic localization and nearby cycles, J. Algebraic Geom. 28 (2019), 251–289.CrossRefGoogle Scholar
Richarz, T. and Zhu, X., Appendix to The geometrical Satake correspondence for ramified groups, Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), fascicule 2.Google Scholar
Rostami, S., The Bernstein presentation for general connected reductive groups, J. Lond. Math. Soc. (2) 91 (2015), 514–536.CrossRefGoogle Scholar
Deligne, P., Cohomologie à supports propres, in Séminaire de Géometrie Algébrique du Bois Marie: Théorie des topos et cohomologie etale des schemas (SGA 4), tome 3, Lecture Notes in Mathematics, vol. 305, eds Artin, M., Grothendieck, A. and Verdier, J. L. (Springer, 1973).Google Scholar
Deligne, P., Séminaire de Géométrie Algébrique du Bois Marie – Cohomologie étale (SGA 4½), Lecture Notes in Mathematics, vol. 569 (Springer, Berlin, 1977).CrossRefGoogle Scholar
Deligne, P. and Katz, N. (eds), Séminaire de Géométrie Algébrique du Bois Marie: Groupes de monodromie en géométrie algébrique (SGA 7) – Vol. 2, Lecture Notes in Mathematics, vol. 340 (Springer, Berlin, 1973).CrossRefGoogle Scholar
Stacks Project, http://stacks.math.columbia.edu/.Google Scholar
Tits, J., Reductive groups over local fields, in Automorphic forms, representations and L-functions, Proceedings of Symposia in Pure Mathematics, Corvallis, OR, 1977, Vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 29–69.CrossRefGoogle Scholar
Zhu, X., On the coherence conjecture of Pappas and Rapoport, Ann. of Math. (2) 180 (2014), 1–85.CrossRefGoogle Scholar
Zhu, X., The geometrical Satake correspondence for ramified groups, Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), fascicule 2. With an appendix by T. Richarz and X. Zhu.Google Scholar
Zhu, X., An introduction to affine Grassmannians and the geometric Satake equivalence, in Geometry of moduli spaces and representation theory, IAS/Park City Mathematics Series, vol. 24 (American Mathematical Society, Providence, RI, 2017), 59–154.CrossRefGoogle Scholar