Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-03T17:39:59.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Support varieties and stable categories for algebraic groups

Part of: Representation theory of groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  27 March 2023

Eric M. Friedlander
Eric M. Friedlander*
Affiliation:
Department of Mathematics, University of Southern California, Los Angeles, CA 90089, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider rational representations of a connected linear algebraic group 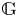$\mathbb {G}$ over a field 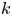$k$ of positive characteristic 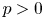$p > 0$. We introduce a natural extension 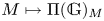$M \mapsto \Pi (\mathbb {G})_M$ to 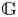$\mathbb {G}$-modules of the 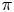$\pi$-point support theory for modules 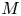$M$ for a finite group scheme 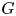$G$ and show that this theory is essentially equivalent to the more ‘intrinsic’ and ‘explicit’ theory 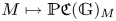$M \mapsto \mathbb {P}\mathfrak{C}(\mathbb {G})_M$ of supports for an algebraic group of exponential type, a theory which uses 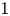$1$-parameter subgroups 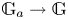$\mathbb {G}_a \to \mathbb {G}$. We extend our support theory to bounded complexes of 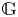$\mathbb {G}$-modules, 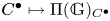$C^\bullet \mapsto \Pi (\mathbb {G})_{C^\bullet }$. We introduce the tensor triangulated category 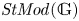$\mathit {StMod}(\mathbb {G})$, the Verdier quotient of the bounded derived category 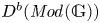$D^b(\mathit {Mod}(\mathbb {G}))$ by the thick subcategory of mock injective modules. Our support theory satisfies all the ‘standard properties’ for a theory of supports for 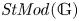$\mathit {StMod}(\mathbb {G})$. As an application, we employ 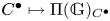$C^\bullet \mapsto \Pi (\mathbb {G})_{C^\bullet }$ to establish the classification of 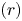$(r)$-complete, thick tensor ideals of 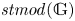$\mathit {stmod}(\mathbb {G})$ in terms of locally 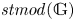$\mathit {stmod}(\mathbb {G})$-realizable subsets of 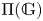$\Pi (\mathbb {G})$ and the classification of 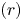$(r)$-complete, localizing subcategories of 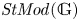$\mathit {StMod}(\mathbb {G})$ in terms of locally 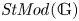$\mathit {StMod}(\mathbb {G})$-realizable subsets of 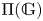$\Pi (\mathbb {G})$.

Keywords

support varietiesstable categoriesalgebraic groups

MSC classification

Primary: 20G05: Representation theory 20C20: Modular representations and characters
Secondary: 20G10: Cohomology theory
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 4 , April 2023 , pp. 746 - 779
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Brian Parshall

The author was partially supported by the Simons Foundation.

References

Avrunin, G. and Scott, L., Quillen stratification for modules, Invent. Math. 66 (1962), 277–286.CrossRefGoogle Scholar
Balmer, P., The spectrum of prime ideals in tensor triangulated categories, J. Reine Angew. Math. 588 (2005), 149–168.CrossRefGoogle Scholar
Benson, D., Carlson, J. and Rickard, J., Thick subcagegories of the stable module category, Fund. Math. 153 (1997), 59–80.CrossRefGoogle Scholar
Benson, D., Iyengar, S., Krause, H. and Pevtsova, J., Stratification for module categories of finite group schemes, J. Amer. Math. Soc. 31 (2018), 265–302.CrossRefGoogle Scholar
Benson, D. and Pevtsova, J., A realization theorem for modules of constant Jordan type and vector bundles, Trans. Amer. Math. Soc. 364 (2012), 6459–6478.CrossRefGoogle Scholar
Carlson, J., The complexity and varieties of modules, Lecture Notes in Mathematics, vol. 882 (Springer, 1981), 415–422.CrossRefGoogle Scholar
Carlson, J., The variety of an indecomposable module is connected, Invent. Math. 77 (1984), 291–299.CrossRefGoogle Scholar
Carlson, J., Friedlander, E. and Pevtsova, J., Modules of constant Jordan type, J. Reine Angew. Math. 614 (2008), 191–234.Google Scholar
Cline, E., Parshall, B. and Scott, L., Induced modules and affine quotients, Math. Ann. 230 (1977), 1–14.CrossRefGoogle Scholar
Cline, E., Parshall, B., Scott, L. and van der Kallen, W., Rational and generic cohomology, Invent. Math. 39 (1977), 143–163.10.1007/BF01390106CrossRefGoogle Scholar
Donkin, S., On projective modules for algebraic groups, J. Lond. Math. Soc. (2) 54 (1996), 75–88.CrossRefGoogle Scholar
Drupieski, C., Nakano, D. and Parshall, B., Differentiaing the Weyl generic dimension formula with applications to support varieties, Adv. Math. 229 (2012), 2656–2668.CrossRefGoogle Scholar
Friedlander, E., Algebraic cycles, Chow varieties, and Lawson homology, Compos. Math. 77 (2011), 55–93.Google Scholar
Friedlander, E., Support varieties for rational representations, Compos. Math. 151 (2015), 765–792.CrossRefGoogle Scholar
Friedlander, E., Filtrations, 1-parameter subgroups, and rational injectivity, Adv. Math. 323 (2018), 84–113.CrossRefGoogle Scholar
Friedlander, E., Cohomology of unipotent group schemes, Algebr. Represent. Theory 22 (2019), 1427–1455.CrossRefGoogle Scholar
Friedlander, E. and Parshall, B., Support varieties for restricted Lie algebras, Invent. Math. 86 (1986), 553–562.CrossRefGoogle Scholar
Friedlander, E. and Pevtsova, J., Representation-theoretic support spaces for finite group schemes, Amer. J. Math. 127 (2005), 379–420.CrossRefGoogle Scholar
Friedlander, E. and Pevtsova, J., $\Pi$-supports for modules for finite group schemes, Duke Math. J. 139 (2007), 317–368.CrossRefGoogle Scholar
Friedlander, E. and Pevtsova, J., Generalized support varieties for finite group schemes, Doc. Math. Extra Volume: Andrei A. Suslin's Sixtieth Birthday (2010), 317–368.Google Scholar
Friedlander, E. and Pevtsova, J., Constructions for infinitesimal group schemes, Trans. Amer. Math. Soc. 363 (2011), 6007–6061.CrossRefGoogle Scholar
Friedlander, E., Pevtsova, J. and Suslin, A., Generic and Jordan types, Invent. Math. 168 (2007), 485–522.10.1007/s00222-007-0037-2CrossRefGoogle Scholar
Happel, D., Triangulated categories in the representation theory of finite dimensional algebras, London Mathematical Society Lecture Note Series, vol. 119 (Cambridge University Press, 1988).CrossRefGoogle Scholar
Hardesty, W., Nakano, D. and Sobaje, P., On the existence of mock injective modules for algebraic groups, Bull. Lond. Math. Soc. 49 (2017), 806–817.CrossRefGoogle Scholar
Jantzen, J. C., Representations of Algebraic groups, second edition, Mathematical Surveys and Monographs, vol. 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
McNinch, G., Abelian unipotent subgroups of reductive groups, J. Pure Appl. Algebra 167 (2002), 260–300.CrossRefGoogle Scholar
Nakano, D., Parshall, B. J. and Vella, D. C., Support varieties for algebraic groups, J. Reine Angew. Math. 547 (2002), 15–49.Google Scholar
Neeman, A., Triangulated categories, Annals of Mathematics Studies, vol. 148 (Princeton University Press, Princeton, NJ, 2001).CrossRefGoogle Scholar
Pevtsova, J., Infinite dimensional modules for Frobenius kernels, J. Pure Appl. Algebra 173 (2002), 59–86.10.1016/S0022-4049(01)00168-2CrossRefGoogle Scholar
Quillen, D., The spectrum of an equivariant cohomology ring. I, II, Ann. of Math. (2) 94 (1971), 549–572, 573–602.CrossRefGoogle Scholar
Rickard, J., Derived categories and stable equivalence, J. Pure Appl. Algebra 61 (1989), 303–317.10.1016/0022-4049(89)90081-9CrossRefGoogle Scholar
Rickard, J., Idempotent modules in the stale category, J. Lond. Math. Soc. (2) 56 (1997), 149–170.CrossRefGoogle Scholar
Seitz, G., Unipotent elements, tilting modules, and saturation, Invent. Math. 141 (2000), 467–502.CrossRefGoogle Scholar
Sobaje, P., Support varieties for Frobenius kernels of classical groups, J. Pure Appl. Algebra 216 (2013), 2657–2664.CrossRefGoogle Scholar
Suslin, A., Friedlander, E. and Bendel, C., Infinitesimal 1-parameter subgroups and cohomology, J. Amer. Math. Soc. 10 (1997), 693–728.CrossRefGoogle Scholar
Suslin, A., Friedlander, E. and Bendel, C., Support varieties for infinitesimal group schemes, J. Amer. Math. Soc. 10 (1997), 729–759.CrossRefGoogle Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, 1994).CrossRefGoogle Scholar