Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T15:07:08.295Z Has data issue: false hasContentIssue false
  • English
  • Français

Successive minima and asymptotic slopes in Arakelov geometry

Part of: Arithmetic algebraic geometry Geometry of numbers Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  10 June 2021

François Ballaÿ
François Ballaÿ*
Affiliation:
Beijing International Center for Mathematical Research, Peking University, 5 Yi He Yuan Road, Beijing100871, PR [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 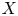$X$ be a normal and geometrically integral projective variety over a global field 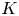$K$ and let 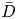$\bar {D}$ be an adelic 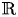${\mathbb {R}}$-Cartier divisor on 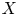$X$. We prove a conjecture of Chen, showing that the essential minimum 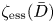$\zeta _{\mathrm {ess}}(\bar {D})$ of 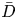$\bar {D}$ equals its asymptotic maximal slope under mild positivity assumptions. As an application, we see that 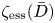$\zeta _{\mathrm {ess}}(\bar {D})$ can be read on the Okounkov body of the underlying divisor 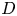$D$ via the Boucksom–Chen concave transform. This gives a new interpretation of Zhang's inequalities on successive minima and a criterion for equality generalizing to arbitrary projective varieties a result of Burgos Gil, Philippon and Sombra concerning toric metrized divisors on toric varieties. When applied to a projective space 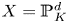$X = {\mathbb {P}}_K^{d}$, our main result has several applications to the study of successive minima of hermitian vector spaces. We obtain an absolute transference theorem with a linear upper bound, answering a question raised by Gaudron. We also give new comparisons between successive slopes and absolute minima, extending results of Gaudron and Rémond.

Keywords

heightessential minimumsuccessive minimaadelic line bundles and divisorsOkounkov bodieshermitian vector bundlestransference theorems

MSC classification

Primary: 14G40: Arithmetic varieties and schemes; Arakelov theory; heights
Secondary: 11G50: Heights 11H06: Lattices and convex bodies
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 6 , June 2021 , pp. 1302 - 1339
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, M. H. and Rumely, R., Equidistribution of small points, rational dynamics, and potential theory, Ann. Inst. Fourier (Grenoble) 56 (2006), 625–688.CrossRefGoogle Scholar
Banaszczyk, W., New bounds in some transference theorems in the geometry of numbers, Math. Ann. 296 (1993), 625–635.CrossRefGoogle Scholar
Berman, R. and Boucksom, S., Growth of balls of holomorphic sections and energy at equilibrium, Invent. Math. 181 (2010), 337–394.CrossRefGoogle Scholar
Bombieri, E. and Vaaler, J., On Siegel's lemma, Invent. Math. 73 (1983), 11–32.CrossRefGoogle Scholar
Bosser, V. and Gaudron, É., Logarithmes des points rationnels des variétés abéliennes, Canad. J. Math. 71 (2019), 247–298.10.4153/CJM-2018-005-7CrossRefGoogle Scholar
Boucksom, S. and Chen, H., Okounkov bodies of filtered linear series, Compos. Math. 147 (2011), 1205–1229.CrossRefGoogle Scholar
Boucksom, S., Demailly, J.-P., Păun, M. and Peternell, T., The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension, J. Algebraic Geom. 22 (2013), 201–248.CrossRefGoogle Scholar
Burgos Gil, J. I., Moriwaki, A., Philippon, P. and Sombra, M., Arithmetic positivity on toric varieties, J. Algebraic Geom. 25 (2016), 201–272.CrossRefGoogle Scholar
Burgos Gil, J. I., Philippon, P., Rivera-Letelier, J. and Sombra, M., The distribution of Galois orbits of points of small height in toric varieties, Amer. J. Math. 141 (2019), 309–381.Google Scholar
Burgos Gil, J. I., Philippon, P. and Sombra, M., Arithmetic geometry of toric varieties. Metrics, measures and heights, Astérisque 360 (2014).Google Scholar
Burgos Gil, J. I., Philippon, P. and Sombra, M., Successive minima of toric height functions, Ann. Inst. Fourier (Grenoble) 65 (2015), 2145–2197.CrossRefGoogle Scholar
Chambert-Loir, A., Mesures et équidistribution sur les espaces de Berkovich, J. Reine Angew. Math. 595 (2006), 215–235.Google Scholar
Charles, F., Arithmetic ampleness and an arithmetic Bertini theorem. Preprint (2017), arXiv:1703.02481.Google Scholar
Chen, H., Arithmetic Fujita approximation, Ann. Sci. Éc. Norm. Supér. (4) 43 (2010), 555–578.CrossRefGoogle Scholar
Chen, H., Convergence des polygones de Harder-Narasimhan, Mém. Soc. Math. Fr. (N.S.) 120 (2010), 116.Google Scholar
Chen, H., Differentiability of the arithmetic volume function, J. Lond. Math. Soc. (2) 84 (2011), 365–384.CrossRefGoogle Scholar
Chen, H., Majorations explicites des fonctions de Hilbert-Samuel géométrique et arithmétique, Math. Z. 279 (2015), 99–137.CrossRefGoogle Scholar
Chen, H., Sur la comparaison entre les minima et les pentes, Publ. Math. Besançon Algèbre Théorie Nr. 2018 (2018), 5–23.Google Scholar
Chen, H., Comparison of some invariants of Euclidean lattices, in Proceedings of the International Congress of Chinese Mathematicians (2019), to appear. Preprint (2019), https://webusers.imj-prg.fr/~huayi.chen/Recherche/iccm2019_chen.pdf.Google Scholar
Chen, H. and Moriwaki, A., Algebraic dynamical systems and Dirichlet's unit theorem on arithmetic varieties, Int. Math. Res. Not. IMRN 2015 (2015), 13669–13716.CrossRefGoogle Scholar
Chen, H. and Moriwaki, A., Arakelov geometry over adelic curves, Lecture Notes in Mathematics, vol. 2258 (Springer, 2019).Google Scholar
Cutkosky, S. D., Teissier's problem on inequalities of nef divisors, J. Algebra Appl. 14 (2015), 1540002.CrossRefGoogle Scholar
Das, O., Finiteness of log minimal models and nef curves on $3$-folds in characteristic $p>5$, Nagoya Math. J. 239 (2020), 76–109.CrossRefGoogle Scholar
Detemple, D. W., The non-integer property of sums of reciprocals of successive integers, Math. Gazette 75 (1991), 193–194.CrossRefGoogle Scholar
Favre, C. and Rivera-Letelier, J., Equidistribution quantitative des points de petite hauteur sur la droite projective, Math. Ann. 335 (2006), 311–361.CrossRefGoogle Scholar
Gaudron, É., Pentes des fibrés vectoriels adéliques sur un corps global, Rend. Semin. Mat. Univ. Padova 119 (2008), 21–95.CrossRefGoogle Scholar
Gaudron, É., Minima and slopes of rigid adelic spaces, in Arakelov geometry and Diophantine applications, Lecture Notes in Mathematics, vol. 2276, ed. G. Rémond and E. Peyre (Springer, 2020).Google Scholar
Gaudron, É. and Rémond, G., Minima, pentes et algèbre tensorielle, Israel J. Math. 195 (2013), 565–591.CrossRefGoogle Scholar
Gaudron, É. and Rémond, G., Polarisations et isogénies, Duke Math. J. 163 (2014), 2057–2108.CrossRefGoogle Scholar
Gaudron, É. and Rémond, G., Corps de Siegel, J. Reine Angew. Math. 726 (2017), 187–247.Google Scholar
Gubler, W., The Bogomolov conjecture for totally degenerate abelian varieties, Invent. Math. 169 (2007), 377–400.CrossRefGoogle Scholar
Gubler, W., Equidistribution over function fields, Manuscripta Math. 127 (2008), 485–510.CrossRefGoogle Scholar
Ikoma, H., A Bertini-type theorem for free arithmetic linear series, Kyoto J. Math. 55 (2015), 531–541.CrossRefGoogle Scholar
Ikoma, H., On the concavity of the arithmetic volumes, Int. Math. Res. Not. IMRN 2015 (2015), 7063–7109.CrossRefGoogle Scholar
Kaveh, K. and Khovanskii, A. G., Newton-Okounkov bodies, semigroups of integral points, graded algebras and intersection theory, Ann. of Math. (2) 176 (2012), 925–978.CrossRefGoogle Scholar
Lazarsfeld, R., Positivity in algebraic geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 48 (Springer, Berlin, 2004).Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry. II, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 49 (Springer, Berlin, 2004).Google Scholar
Lazarsfeld, R. and Mustaţă, M., Convex bodies associated to linear series, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 783–835.CrossRefGoogle Scholar
Moriwaki, A., Arithmetic Bogomolov-Gieseker's inequality, Amer. J. Math. 117 (1995), 1325–1347.CrossRefGoogle Scholar
Moriwaki, A., Relative Bogomolov's inequality and the cone of positive divisors on the moduli space of stable curves, J. Amer. Math. Soc. 11 (1998), 569–600.CrossRefGoogle Scholar
Moriwaki, A., Arithmetic linear series with base conditions, Math. Z. 272 (2012), 1383–1401.CrossRefGoogle Scholar
Moriwaki, A., Zariski decompositions on arithmetic surfaces, Publ. Res. Inst. Math. Sci. 48 (2012), 799–898.CrossRefGoogle Scholar
Moriwaki, A., Adelic divisors on arithmetic varieties, Mem. Amer. Math. Soc. 242 (2016).Google Scholar
Pekker, A., On successive minima and the absolute Siegel's lemma, J. Number Theory 128 (2008), 564–575.CrossRefGoogle Scholar
Roy, D. and Thunder, J. L., An absolute Siegel's lemma, J. Reine Angew. Math. 476 (1996), 1–26.Google Scholar
Szpiro, L., Ullmo, E. and Zhang, S., Équirépartition des petits points, Invent. Math. 127 (1997), 337–347.CrossRefGoogle Scholar
Yuan, X., Big line bundles over arithmetic varieties, Invent. Math. 173 (2008), 603–649.CrossRefGoogle Scholar
Zhang, S., Positive line bundles on arithmetic varieties, J. Amer. Math. Soc. 8 (1995), 187–221.CrossRefGoogle Scholar
Zhang, S., Small points and adelic metrics, J. Algebraic Geom. 4 (1995), 281–300.Google Scholar