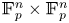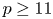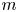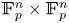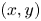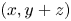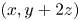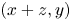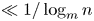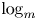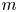1. Introduction
Szemerédi's famous theorem on arithmetic progressions, which states that any subset of the integers with positive upper density contains arbitrarily long arithmetic progressions, has the following multidimensional generalization due to Furstenberg and Katznelson [Reference Furstenberg and KatznelsonFK78].
Theorem 1.1 Let ![]() $X$ be a finite, nonempty subset of
$X$ be a finite, nonempty subset of ![]() $\mathbb {Z}^d$. If
$\mathbb {Z}^d$. If ![]() $S\subset [N]^d$ contains no nontrivial homothetic copy
$S\subset [N]^d$ contains no nontrivial homothetic copy ![]() $a+bX$ of
$a+bX$ of ![]() $X$, then
$X$, then ![]() $|S|=o(N^d)$.
$|S|=o(N^d)$.
Here we use the standard notation ![]() $[N]:=\{1,\ldots,N\}$. There has been great interest over the past few decades in proving a quantitative version of this theorem with reasonable bounds, i.e. with an upper bound for
$[N]:=\{1,\ldots,N\}$. There has been great interest over the past few decades in proving a quantitative version of this theorem with reasonable bounds, i.e. with an upper bound for ![]() $|S|$ whose savings over the trivial bound of
$|S|$ whose savings over the trivial bound of ![]() $N^d$ grows at least as quickly as a finite number of iterated logarithms. Indeed, Gowers has posed the problem of proving such a result on several occasions [Reference GowersGow98a, Reference GowersGow01a, Reference GowersGow01b], and others, such as Graham [Reference GrahamGra97], have asked for bounds for sets lacking particular multidimensional configurations. While reasonable bounds are known in Szemerédi's theorem due to work of Gowers [Reference GowersGow98b, Reference GowersGow01b], none are known in the Furstenberg–Katznelson theorem in general. Furstenberg and Katznelson's original proof, which was via ergodic theory, produces no explicit bounds, while the hypergraph regularity proofs of Nagle, Rödl, Schacht, and Skokan [Reference Nagle, Rödl and SchachtNRS06, Reference Rödl and SkokanRS04], Gowers [Reference GowersGow07], and Tao [Reference TaoTao06] each give a saving over the trivial bound of inverse Ackermann type.
$N^d$ grows at least as quickly as a finite number of iterated logarithms. Indeed, Gowers has posed the problem of proving such a result on several occasions [Reference GowersGow98a, Reference GowersGow01a, Reference GowersGow01b], and others, such as Graham [Reference GrahamGra97], have asked for bounds for sets lacking particular multidimensional configurations. While reasonable bounds are known in Szemerédi's theorem due to work of Gowers [Reference GowersGow98b, Reference GowersGow01b], none are known in the Furstenberg–Katznelson theorem in general. Furstenberg and Katznelson's original proof, which was via ergodic theory, produces no explicit bounds, while the hypergraph regularity proofs of Nagle, Rödl, Schacht, and Skokan [Reference Nagle, Rödl and SchachtNRS06, Reference Rödl and SkokanRS04], Gowers [Reference GowersGow07], and Tao [Reference TaoTao06] each give a saving over the trivial bound of inverse Ackermann type.
Reasonable bounds in Theorem 1.1 are currently known for only one genuinely multidimensional configuration: two-dimensional corners
(and, thus, their linear images) due to the work of Shkredov [Reference ShkredovShk06a, Reference ShkredovShk06b], who proved that any subset of ![]() $[N]\times [N]$ containing no nontrivial corners has size at most
$[N]\times [N]$ containing no nontrivial corners has size at most ![]() $\ll N^2/(\log \log {N})^c$ for some absolute constant
$\ll N^2/(\log \log {N})^c$ for some absolute constant ![]() $c>0$. No reasonable bounds are known for any two-or-more-dimensional four-point configuration, such as three-dimensional corners,
$c>0$. No reasonable bounds are known for any two-or-more-dimensional four-point configuration, such as three-dimensional corners,
or axis-aligned squares,
The latter of these two configurations is the topic of a conjecture of Graham [Reference GrahamGra97], which states that any subset ![]() $S\subset \mathbb {N}\times \mathbb {N}$ for which
$S\subset \mathbb {N}\times \mathbb {N}$ for which ![]() $\sum _{(x,y)\in S} {1}/({x^2+y^2})$ diverges must contain an axis-aligned square. Graham also conjectured, more generally, that if
$\sum _{(x,y)\in S} {1}/({x^2+y^2})$ diverges must contain an axis-aligned square. Graham also conjectured, more generally, that if ![]() $\sum _{(x,y)\in S} {1}/({x^2+y^2})$ diverges, then
$\sum _{(x,y)\in S} {1}/({x^2+y^2})$ diverges, then ![]() $S$ must contain a homothetic copy of
$S$ must contain a homothetic copy of ![]() $[m]\times [m]$ for every positive integer
$[m]\times [m]$ for every positive integer ![]() $m$. This is a two-dimensional generalization of the famous and still unresolved conjecture of Erdős that every subset
$m$. This is a two-dimensional generalization of the famous and still unresolved conjecture of Erdős that every subset ![]() $T\subset \mathbb {N}$ for which
$T\subset \mathbb {N}$ for which ![]() $\sum _{n\in T} {1}/{n}$ diverges must contain arbitrarily long arithmetic progressions.
$\sum _{n\in T} {1}/{n}$ diverges must contain arbitrarily long arithmetic progressions.
Proving reasonable bounds for sets lacking the four-point configurations (2) and (3) seems to be out of reach. This is because no one has managed yet to prove anything useful about a certain two-dimensional directional uniformity norm that naturally appears in the study of these configurations. Details on this difficulty can be found in the work of Austin [Reference AustinAus13a, Reference AustinAus13b], where he demonstrates how enormously complicated and difficult even 100% and 99% inverse theorems can be for directional uniformity norms.
The purpose of this paper is to identify the first two-dimensional four-point configuration for which reasonable bounds in the multidimensional Szemerédi theorem can be proven, and to prove such bounds in the finite field model setting. We will study the configuration
which, when plotted on a two-dimensional integer grid, takes the shape of the capital letter ‘L’. Because of this, we refer to (4) as an L-shaped configuration, and an L-shaped configuration with ![]() $z\neq 0$ as a nontrivial L-shaped configuration.
$z\neq 0$ as a nontrivial L-shaped configuration.
Theorem 1.2 There exists a natural number ![]() $m$ and a constant
$m$ and a constant ![]() $C>0$ such that the following holds. Fix a prime
$C>0$ such that the following holds. Fix a prime ![]() $p\geq 11$, and set
$p\geq 11$, and set ![]() $N:=p^n$. If
$N:=p^n$. If ![]() $n\geq C$, then all
$n\geq C$, then all ![]() $S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ containing no nontrivial L-shaped configurations satisfy
$S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ containing no nontrivial L-shaped configurations satisfy
The ![]() $m$ obtained in the theorem is huge, so we do not attempt to compute it. The bulk of the size of
$m$ obtained in the theorem is huge, so we do not attempt to compute it. The bulk of the size of ![]() $m$ comes from our use of a recent quantitative inverse theorem for the
$m$ comes from our use of a recent quantitative inverse theorem for the ![]() $U^{10}$-norm on
$U^{10}$-norm on ![]() $\mathbb {F}_p^n$ due to Gowers and Milićević, who in [Reference Gowers and MilićevićGM20] give a rough upper bound for the number of iterated exponentials appearing in their result. Based on this,
$\mathbb {F}_p^n$ due to Gowers and Milićević, who in [Reference Gowers and MilićevićGM20] give a rough upper bound for the number of iterated exponentials appearing in their result. Based on this, ![]() $m$ is likely at least 24 trillion. The use of this inverse theorem is necessary in our proof, and no amount of care to argue efficiently in the rest of the argument can reduce
$m$ is likely at least 24 trillion. The use of this inverse theorem is necessary in our proof, and no amount of care to argue efficiently in the rest of the argument can reduce ![]() $m$ by much. Thus, we have not tried to optimize the proof of Theorem 1.2, choosing instead to present the simplest argument that gives a reasonable upper bound.
$m$ by much. Thus, we have not tried to optimize the proof of Theorem 1.2, choosing instead to present the simplest argument that gives a reasonable upper bound.
It is likely that the proof of Theorem 1.2 can be adapted to the integer setting to prove a reasonable bound for subsets of ![]() $[N]\times [N]$ lacking L-shaped configurations, with the bound obtained being far more reasonable than the bound in Theorem 1.2. This is because the quantitative aspects of Manners's [Reference MannersMan18] inverse theorem for the
$[N]\times [N]$ lacking L-shaped configurations, with the bound obtained being far more reasonable than the bound in Theorem 1.2. This is because the quantitative aspects of Manners's [Reference MannersMan18] inverse theorem for the ![]() $U^{s}$-norm on cyclic groups are better than those of Gowers and Milićević's inverse theorem when
$U^{s}$-norm on cyclic groups are better than those of Gowers and Milićević's inverse theorem when ![]() $s>4$. It is also likely that Theorem 1.2 can be extended to more general L-shaped configurations with a longer vertical ‘leg’,
$s>4$. It is also likely that Theorem 1.2 can be extended to more general L-shaped configurations with a longer vertical ‘leg’,
in both the finite field model and integer settings. We expect, however, that understanding L-shaped configurations with two longer ‘legs’,
is significantly more difficult, for some of the same reasons that proving reasonable bounds for sets lacking three-dimensional corners or axis-aligned squares seems out of reach.
While progress in proving a quantitative version of the multidimensional Szemerédi theorem has so far been extremely limited, there has been a bit more success in proving reasonable bounds for sets lacking multidimensional configurations with more degrees of freedom than those in Theorem 1.1. Prendiville [Reference PrendivillePre15] has proven reasonable bounds for subsets of ![]() $[N]^d$ lacking any sufficiently nondegenerate three- or four-term matrix progression, and one consequence of his work is that any subset of
$[N]^d$ lacking any sufficiently nondegenerate three- or four-term matrix progression, and one consequence of his work is that any subset of ![]() $[N]\times [N]$ containing no four vertices of any square (not necessarily axis-aligned) has size at most
$[N]\times [N]$ containing no four vertices of any square (not necessarily axis-aligned) has size at most ![]() $\ll N^2/(\log \log {N})^{c'}$ for some absolute constant
$\ll N^2/(\log \log {N})^{c'}$ for some absolute constant ![]() $c'>0$.
$c'>0$.
The remainder of this paper is organized as follows. In § 2, we give a detailed outline of our proof of Theorem 1.2, including statements of the three main components of the density-increment argument: control of the count of L-shaped configurations by directional uniformity norms, obtaining a density increment on a structured set, and pseudorandomizing the structured set obtained previously. After introducing additional technical preliminaries in §§ 3 and 4, we prove these three main components in §§ 5, 6, and 7, respectively. We then carry out the density increment argument in § 8, proving Theorem 1.2.
2. Outline of the proof of Theorem 1.2
We begin this section by introducing the minimum amount of notation and preliminaries needed to understand our proof outline. We will use the standard asymptotic notation ![]() $O,\Omega,$ and
$O,\Omega,$ and ![]() $o$, along with Vinogradov's notation
$o$, along with Vinogradov's notation ![]() $\ll,\gg,$ and
$\ll,\gg,$ and ![]() $\asymp$. For any two quantities
$\asymp$. For any two quantities ![]() $A$ and
$A$ and ![]() $B$, the relations
$B$, the relations ![]() $A=O(B)$,
$A=O(B)$, ![]() $B=\Omega (A)$,
$B=\Omega (A)$, ![]() $A\ll B$, and
$A\ll B$, and ![]() $B\gg A$ all mean that
$B\gg A$ all mean that ![]() $|A|\leq C|B|$ for some absolute constant
$|A|\leq C|B|$ for some absolute constant ![]() $C>0$. We will write
$C>0$. We will write ![]() $O(B)$ to represent a quantity that is
$O(B)$ to represent a quantity that is ![]() $\ll B$ and
$\ll B$ and ![]() $\Omega (A)$ to represent a quantity that is
$\Omega (A)$ to represent a quantity that is ![]() $\gg A$. When any of these asymptotic symbols appears with a subscript, the implied constant is allowed to depend on the parameters in the subscript. Since we fix a prime
$\gg A$. When any of these asymptotic symbols appears with a subscript, the implied constant is allowed to depend on the parameters in the subscript. Since we fix a prime ![]() $p$ in Theorem 1.2, the implied constants appearing throughout the paper will sometimes depend on
$p$ in Theorem 1.2, the implied constants appearing throughout the paper will sometimes depend on ![]() $p$ even though we will not alert the reader to this with a subscript. We will use
$p$ even though we will not alert the reader to this with a subscript. We will use ![]() $\log _m$ to denote the
$\log _m$ to denote the ![]() $m$-fold iterated logarithm, so that
$m$-fold iterated logarithm, so that ![]() $\log _1:=\log$ and
$\log _1:=\log$ and ![]() $\log _{i}:=\log \circ \log _{i-1}$ for all
$\log _{i}:=\log \circ \log _{i-1}$ for all ![]() $i>1$, as well as
$i>1$, as well as ![]() $\exp ^m$ to denote the
$\exp ^m$ to denote the ![]() $m$-fold iterated exponential, so that
$m$-fold iterated exponential, so that ![]() $\exp ^1=\exp$ and
$\exp ^1=\exp$ and ![]() $\exp ^{i}:=\exp \circ \exp ^{i-1}$ for all
$\exp ^{i}:=\exp \circ \exp ^{i-1}$ for all ![]() $i>1$.
$i>1$.
We will frequently denote the indicator function of a set ![]() $A$ by the letter
$A$ by the letter ![]() $A$ itself, so that
$A$ itself, so that
 \[ A(x):=\begin{cases} 1 & x\in A \\ 0 & x\notin A. \end{cases} \]
\[ A(x):=\begin{cases} 1 & x\in A \\ 0 & x\notin A. \end{cases} \]
For any pair of finite sets ![]() $X\subset Y$ with
$X\subset Y$ with ![]() $Y\neq \emptyset$, we denote the density of
$Y\neq \emptyset$, we denote the density of ![]() $X$ in
$X$ in ![]() $Y$ by
$Y$ by
For any function ![]() $f:X\to \mathbb {C}$, we denote the average of
$f:X\to \mathbb {C}$, we denote the average of ![]() $f$ over
$f$ over ![]() $X$ by
$X$ by
When ![]() $X=\mathbb {F}_p^n$, we will usually drop ‘
$X=\mathbb {F}_p^n$, we will usually drop ‘![]() $\in X$’ and just write
$\in X$’ and just write ![]() $\mathbb {E}_x$ for
$\mathbb {E}_x$ for ![]() $\mathbb {E}_{x\in \mathbb {F}_p^n}$. Whenever
$\mathbb {E}_{x\in \mathbb {F}_p^n}$. Whenever ![]() $f$ satisfies
$f$ satisfies ![]() $|f(x)|\leq 1$ for all
$|f(x)|\leq 1$ for all ![]() $x$ in its domain, we say that it is
$x$ in its domain, we say that it is ![]() $1$-bounded. Note that the indicator function of any set is
$1$-bounded. Note that the indicator function of any set is ![]() $1$-bounded.
$1$-bounded.
For any ![]() $f:\mathbb {F}_p^n\to \mathbb {C}$ and
$f:\mathbb {F}_p^n\to \mathbb {C}$ and ![]() $\xi \in \mathbb {F}_p^n$, we define the Fourier coefficient of
$\xi \in \mathbb {F}_p^n$, we define the Fourier coefficient of ![]() $f$ at
$f$ at ![]() $\xi$ using the normalization
$\xi$ using the normalization
where ![]() $e_p(z):= e^{2\pi iz/p}$ and
$e_p(z):= e^{2\pi iz/p}$ and ![]() $\cdot$ denotes the usual dot product in
$\cdot$ denotes the usual dot product in ![]() $\mathbb {F}_p^n$. With this choice of normalization, the Fourier inversion formula and Parseval's identity read
$\mathbb {F}_p^n$. With this choice of normalization, the Fourier inversion formula and Parseval's identity read
and
respectively.
Let ![]() $H$ be any abelian group and
$H$ be any abelian group and ![]() $g:H\to \mathbb {C}$. For any
$g:H\to \mathbb {C}$. For any ![]() $h\in H$, we define the function
$h\in H$, we define the function ![]() $\Delta _hg:H\to \mathbb {C}$ by
$\Delta _hg:H\to \mathbb {C}$ by
and, for any ![]() $h_1,\ldots,h_s\in H$, define the
$h_1,\ldots,h_s\in H$, define the ![]() $s$-fold iterated differencing operator
$s$-fold iterated differencing operator ![]() $\Delta _{h_1,\ldots,h_s}$ by
$\Delta _{h_1,\ldots,h_s}$ by
Note that ![]() $\Delta _{h_1,\ldots,h_s}g=\Delta _{h_{\sigma (1)},\ldots,h_{\sigma (s)}}g$ for any permutation
$\Delta _{h_1,\ldots,h_s}g=\Delta _{h_{\sigma (1)},\ldots,h_{\sigma (s)}}g$ for any permutation ![]() $\sigma$ of
$\sigma$ of ![]() $\{1,\ldots,s\}$.
$\{1,\ldots,s\}$.
Now we can recall the definition of the Gowers uniformity norms.
Definition 2.1 Let ![]() $s\in \mathbb {N}$,
$s\in \mathbb {N}$, ![]() $H$ be an abelian group, and
$H$ be an abelian group, and ![]() $f:H\to \mathbb {C}$. The
$f:H\to \mathbb {C}$. The ![]() $U^s$-norm of
$U^s$-norm of ![]() $f$ is defined by
$f$ is defined by
The basic properties of these norms can be found in [Reference TaoTao12]. One such fact needed in the upcoming outline is the inverse theorem for the ![]() $U^2$-norm, which is a simple consequence of Fourier inversion and Parseval's identity.
$U^2$-norm, which is a simple consequence of Fourier inversion and Parseval's identity.
Lemma 2.2 Let ![]() $H$ be an abelian group and
$H$ be an abelian group and ![]() $f:H\to \mathbb {C}$ be
$f:H\to \mathbb {C}$ be ![]() $1$-bounded. If
$1$-bounded. If ![]() $\|f\|_{U^2(H)}\geq \delta$, then there exists a
$\|f\|_{U^2(H)}\geq \delta$, then there exists a ![]() $\psi \in \widehat {H}$ such that
$\psi \in \widehat {H}$ such that
We will also sometimes need the notion of the ![]() $U^2$-norm on an affine subspace
$U^2$-norm on an affine subspace ![]() $w+V$ of
$w+V$ of ![]() $\mathbb {F}_p^n$, which is defined by
$\mathbb {F}_p^n$, which is defined by ![]() $\|f\|_{U^2(w+V)}:=\|f(\cdot -w)\|_{U^2(V)}$. The corresponding inverse theorem for these norms follows from Lemma 2.2.
$\|f\|_{U^2(w+V)}:=\|f(\cdot -w)\|_{U^2(V)}$. The corresponding inverse theorem for these norms follows from Lemma 2.2.
2.1 A review of Shkredov's argument in the finite field model setting
Before we outline the proof of Theorem 1.2, it will be instructive to review Shkredov's argument for corners (1) in the finite field model setting. A detailed account of the argument can be found in the expositions of Green [Reference GreenGre05a, Reference GreenGre05b].
Shkredov's proof proceeds via a density-increment argument. As in all analytic approaches to Szemerédi's theorem and its generalizations, we begin by defining a multilinear average over the configuration of interest. For ![]() $g_0,g_1,g_2:\mathbb {F}_p^n\times \mathbb {F}_p^n\to \mathbb {C}$, set
$g_0,g_1,g_2:\mathbb {F}_p^n\times \mathbb {F}_p^n\to \mathbb {C}$, set
Then, for any ![]() $S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$, the quantity
$S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$, the quantity ![]() $\Lambda _{\llcorner }(S,S,S)$ equals the normalized count,
$\Lambda _{\llcorner }(S,S,S)$ equals the normalized count,
of the number of corners in ![]() $S$. Setting
$S$. Setting ![]() $N:=p^n=|\mathbb {F}_p^n|$, we let
$N:=p^n=|\mathbb {F}_p^n|$, we let ![]() $\sigma :=|S|/N^2$ denote the density of
$\sigma :=|S|/N^2$ denote the density of ![]() $S$ in
$S$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ and
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ and ![]() $g_S:=S-\sigma$ denote the balanced function of
$g_S:=S-\sigma$ denote the balanced function of ![]() $S$. It follows from the trilinearity of
$S$. It follows from the trilinearity of ![]() $\Lambda _{\llcorner }$ that
$\Lambda _{\llcorner }$ that
Since ![]() $\Lambda _{\llcorner }(1,S,S)\geq \sigma ^2$ by the Cauchy–Schwarz inequality, if the normalized count of corners in
$\Lambda _{\llcorner }(1,S,S)\geq \sigma ^2$ by the Cauchy–Schwarz inequality, if the normalized count of corners in ![]() $S$ is far below the
$S$ is far below the ![]() $\sim \sigma ^3$ expected for a random set of density
$\sim \sigma ^3$ expected for a random set of density ![]() $\sigma$, which is the case when
$\sigma$, which is the case when ![]() $S$ has no nontrivial corners and
$S$ has no nontrivial corners and ![]() $N$ is sufficiently large in terms of
$N$ is sufficiently large in terms of ![]() $\sigma$, then
$\sigma$, then ![]() $|\Lambda _{\llcorner }(g_S,S,S)|$ must be large.
$|\Lambda _{\llcorner }(g_S,S,S)|$ must be large.
It can then be shown, by an appropriate sequence of applications of the Cauchy–Schwarz inequality, that ![]() $g_S$ must have large box norm
$g_S$ must have large box norm
If ![]() $\|g_S\|_{\square }$ is large, it follows by an averaging argument that
$\|g_S\|_{\square }$ is large, it follows by an averaging argument that ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\sigma ^{O(1)})$ on a product set
$\sigma +\Omega (\sigma ^{O(1)})$ on a product set ![]() $A\times B$ for some large
$A\times B$ for some large ![]() $A,B\subset \mathbb {F}_p^n$.
$A,B\subset \mathbb {F}_p^n$.
One may then hope to continue the density-increment argument by proving the following generalization of the result just sketched: if ![]() $S$ is a subset of density
$S$ is a subset of density ![]() $\sigma$ of a product set
$\sigma$ of a product set ![]() $T=A\times B$ and contains no nontrivial corners, then
$T=A\times B$ and contains no nontrivial corners, then ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\sigma ^{O(1)})$ on a product set
$\sigma +\Omega (\sigma ^{O(1)})$ on a product set ![]() $T'$ contained in
$T'$ contained in ![]() $T$.
$T$.
It turns out, however, that the Cauchy–Schwarz argument mentioned previously yields a lower bound on the box norm of large enough size only when ![]() $A$ and
$A$ and ![]() $B$ are sufficiently Fourier pseudorandom, meaning that their balanced functions
$B$ are sufficiently Fourier pseudorandom, meaning that their balanced functions ![]() $A-|A|/N$ and
$A-|A|/N$ and ![]() $B-|B|/N$ both have small
$B-|B|/N$ both have small ![]() $U^2$-norm. The components of the product set just obtained are essentially arbitrary aside from being large. They are, in particular, not guaranteed to be Fourier pseudorandom.
$U^2$-norm. The components of the product set just obtained are essentially arbitrary aside from being large. They are, in particular, not guaranteed to be Fourier pseudorandom.
To overcome this difficulty, Shkredov introduced a pseudorandomizing step into his proof. He used an energy increment argument incorporating the ![]() $U^2$-inverse theorem to partition
$U^2$-inverse theorem to partition ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ into products of large affine subspaces of the form
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ into products of large affine subspaces of the form
for most of which the sets ![]() $(A-u)\cap V$ and
$(A-u)\cap V$ and ![]() $(B-w)\cap V$ are Fourier pseudorandom in
$(B-w)\cap V$ are Fourier pseudorandom in ![]() $V$. By an averaging argument, there must exist such a product of affine subspaces (5) on which the restrictions of
$V$. By an averaging argument, there must exist such a product of affine subspaces (5) on which the restrictions of ![]() $A$ and
$A$ and ![]() $B$ are both sufficiently dense and Fourier pseudorandom, and such that
$B$ are both sufficiently dense and Fourier pseudorandom, and such that ![]() $S$ still has increased density
$S$ still has increased density ![]() $\sigma +\Omega (\sigma ^{O(1)})$ on the intersection of
$\sigma +\Omega (\sigma ^{O(1)})$ on the intersection of ![]() $T$ with
$T$ with ![]() $(u+V)\times (w+V)$.
$(u+V)\times (w+V)$.
By passing to this product of cosets and using that corners are preserved by translation and invertible linear transformations of the form ![]() $(x,y)\mapsto (Ex,Ey)$, one can then continue the density-increment argument with
$(x,y)\mapsto (Ex,Ey)$, one can then continue the density-increment argument with ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ replaced by
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ replaced by ![]() $\mathbb {F}_p^{n'}\times \mathbb {F}_p^{n'}$, where
$\mathbb {F}_p^{n'}\times \mathbb {F}_p^{n'}$, where ![]() $n'=\dim {V}$. If
$n'=\dim {V}$. If ![]() $S\subset T$ contains no nontrivial corners and
$S\subset T$ contains no nontrivial corners and ![]() $A$ and
$A$ and ![]() $B$ are sufficiently Fourier pseudorandom, then
$B$ are sufficiently Fourier pseudorandom, then ![]() $g_S$ must have large box norm localized to
$g_S$ must have large box norm localized to ![]() $T$. One must then prove that
$T$. One must then prove that ![]() $S$ has a further density increment on a product set contained in
$S$ has a further density increment on a product set contained in ![]() $T$, which is, fortunately, of exactly the same difficulty whether
$T$, which is, fortunately, of exactly the same difficulty whether ![]() $T=\mathbb {F}_p^n\times \mathbb {F}_p^n$ or some other large product set. By applying the pseudorandomizing procedure to the factors of the product set just produced, one can then deduce that if
$T=\mathbb {F}_p^n\times \mathbb {F}_p^n$ or some other large product set. By applying the pseudorandomizing procedure to the factors of the product set just produced, one can then deduce that if ![]() $S$ is a subset of density
$S$ is a subset of density ![]() $\sigma$ of a product set
$\sigma$ of a product set ![]() $T=A\times B$, where
$T=A\times B$, where ![]() $A$ and
$A$ and ![]() $B$ are large and sufficiently Fourier pseudorandom, and
$B$ are large and sufficiently Fourier pseudorandom, and ![]() $S$ contains no nontrivial corners, then
$S$ contains no nontrivial corners, then ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\sigma ^{O(1)})$ on a product set
$\sigma +\Omega (\sigma ^{O(1)})$ on a product set ![]() $T'=A'\times B'$ contained in
$T'=A'\times B'$ contained in ![]() $T$, where
$T$, where ![]() $A'$ and
$A'$ and ![]() $B'$ are also large and sufficiently Fourier pseudorandom. The density increment iteration can be carried out repeatedly to produce a good bound for subsets of
$B'$ are also large and sufficiently Fourier pseudorandom. The density increment iteration can be carried out repeatedly to produce a good bound for subsets of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ lacking corners.
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ lacking corners.
2.2 An outline of our argument
The obstructions to uniformity for L-shaped configurations are not just (skew) product sets, as was the case for corners, but also very general sets of the form
where each ![]() $u_x+V_x$ is an affine subspace of
$u_x+V_x$ is an affine subspace of ![]() $\mathbb {F}_p^n$. For example, assume that
$\mathbb {F}_p^n$. For example, assume that ![]() $n\geq 3$, and consider the set
$n\geq 3$, and consider the set
This set has density
in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$, but
$\mathbb {F}_p^n\times \mathbb {F}_p^n$, but
L-shaped configurations, in contrast to the ![]() $\sim N^3/p^4$ expected in a random subset of
$\sim N^3/p^4$ expected in a random subset of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ of density
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ of density ![]() $1/p$. Similarly, the number of L-shaped configurations in the sets
$1/p$. Similarly, the number of L-shaped configurations in the sets
and
where ![]() $\phi (x)\in \mathbb {F}_p^n$ and
$\phi (x)\in \mathbb {F}_p^n$ and ![]() $u(x)\in \mathbb {F}_p$ are now chosen uniformly at random, is also
$u(x)\in \mathbb {F}_p$ are now chosen uniformly at random, is also ![]() ${\sim }N^3/p^3$ with high probability, while the sets have density
${\sim }N^3/p^3$ with high probability, while the sets have density ![]() ${\sim }1/p$ with high probability. These new sorts of obstructions to uniformity are the main reason why the study of L-shaped configurations is significantly more difficult than that of corners, and must be taken into account to prove Theorem 1.2.
${\sim }1/p$ with high probability. These new sorts of obstructions to uniformity are the main reason why the study of L-shaped configurations is significantly more difficult than that of corners, and must be taken into account to prove Theorem 1.2.
For any functions ![]() $g_0,g_1,g_2,g_3:\mathbb {F}_p^n\times \mathbb {F}_p^n\to \mathbb {C}$, we define
$g_0,g_1,g_2,g_3:\mathbb {F}_p^n\times \mathbb {F}_p^n\to \mathbb {C}$, we define
so that ![]() $\Lambda (S,S,S,S)$ equals the normalized count of L-shaped configurations in any subset
$\Lambda (S,S,S,S)$ equals the normalized count of L-shaped configurations in any subset ![]() $S$ of
$S$ of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$. The multilinearity of
$\mathbb {F}_p^n\times \mathbb {F}_p^n$. The multilinearity of ![]() $\Lambda$ implies that
$\Lambda$ implies that
where, as before, ![]() $g_S=S-\sigma$ is the balanced function of
$g_S=S-\sigma$ is the balanced function of ![]() $S$. Thus, if the normalized count of L-shaped configurations in
$S$. Thus, if the normalized count of L-shaped configurations in ![]() $S$ is far from the random normalized count
$S$ is far from the random normalized count ![]() $\sigma ^4$, one of
$\sigma ^4$, one of ![]() $|\Lambda (1,1,g_S,S)|$,
$|\Lambda (1,1,g_S,S)|$, ![]() $|\Lambda (1,g_S,S,S)|$, or
$|\Lambda (1,g_S,S,S)|$, or ![]() $|\Lambda (g_S,S,S,S)|$ must be large. In particular, when
$|\Lambda (g_S,S,S,S)|$ must be large. In particular, when ![]() $S$ contains no nontrivial L-shaped configurations and
$S$ contains no nontrivial L-shaped configurations and ![]() $N$ is sufficiently large in terms of
$N$ is sufficiently large in terms of ![]() $\sigma$, one of these quantities will be larger than
$\sigma$, one of these quantities will be larger than ![]() $\sigma ^4/2$. It then follows from several applications of the Cauchy–Schwarz inequality that one of the following directional uniformity norms of
$\sigma ^4/2$. It then follows from several applications of the Cauchy–Schwarz inequality that one of the following directional uniformity norms of ![]() $g_S$ must be larger than
$g_S$ must be larger than ![]() $\sigma ^4/2$:
$\sigma ^4/2$:
or
Here ![]() $\|\cdot \|_{\star _3}$ is only a semi-norm, while
$\|\cdot \|_{\star _3}$ is only a semi-norm, while ![]() $\|\cdot \|_{\star _1}$ and
$\|\cdot \|_{\star _1}$ and ![]() $\|\cdot \|_{\star _2}$ are genuine norms. Since these are all Gowers box norms, one can find a proof that they are (semi-)norms in Appendix B of [Reference Green and TaoGT10]. The norm
$\|\cdot \|_{\star _2}$ are genuine norms. Since these are all Gowers box norms, one can find a proof that they are (semi-)norms in Appendix B of [Reference Green and TaoGT10]. The norm ![]() $\|\cdot \|_{\star _1}$ had been studied previously, in the setting of cyclic groups, in work of Shkredov [Reference ShkredovShk09].
$\|\cdot \|_{\star _1}$ had been studied previously, in the setting of cyclic groups, in work of Shkredov [Reference ShkredovShk09].
Directional uniformity norms with two differencing parameters,
for fixed nonzero ![]() $v_1,v_2\in H\times H$, are well-understood. Either
$v_1,v_2\in H\times H$, are well-understood. Either ![]() $v_1$ and
$v_1$ and ![]() $v_2$ are scalar multiples of each other, in which case the norm is just the
$v_2$ are scalar multiples of each other, in which case the norm is just the ![]() $U^2$-norm on
$U^2$-norm on ![]() $\langle v_1\rangle$ averaged over cosets of
$\langle v_1\rangle$ averaged over cosets of ![]() $\langle v_1\rangle$, or they are linearly independent, as in the definition of
$\langle v_1\rangle$, or they are linearly independent, as in the definition of ![]() $\|\cdot \|_{\star _2}$, in which case the norm is, after a change of variables, equivalent to the two-dimensional box norm. Directional uniformity norms with three differencing parameters,
$\|\cdot \|_{\star _2}$, in which case the norm is, after a change of variables, equivalent to the two-dimensional box norm. Directional uniformity norms with three differencing parameters,
for fixed nonzero ![]() $v_1,v_2,v_3\in H\times H$ analogously fall into one of three cases: either
$v_1,v_2,v_3\in H\times H$ analogously fall into one of three cases: either ![]() $v_1,v_2,$ and
$v_1,v_2,$ and ![]() $v_3$ are collinear, lie on exactly two lines, or are in general position. In the first case, the norm is just the
$v_3$ are collinear, lie on exactly two lines, or are in general position. In the first case, the norm is just the ![]() $U^3$-norm on
$U^3$-norm on ![]() $\langle v_1\rangle$ averaged over cosets of
$\langle v_1\rangle$ averaged over cosets of ![]() $\langle v_1\rangle$. In the third case, the norm is linearly equivalent to the intractable norm that arises in the study of three-dimensional corners and axis-aligned squares. The norm
$\langle v_1\rangle$. In the third case, the norm is linearly equivalent to the intractable norm that arises in the study of three-dimensional corners and axis-aligned squares. The norm ![]() $\|\cdot \|_{\star _1}$ we encounter falls into the second case, and the study and fruitful use of this norm turns out to be possible (though still complicated) due to its structure as a ‘
$\|\cdot \|_{\star _1}$ we encounter falls into the second case, and the study and fruitful use of this norm turns out to be possible (though still complicated) due to its structure as a ‘![]() $U^1\times U^2$-norm’.
$U^1\times U^2$-norm’.
The upshot is that if ![]() $S$ contains no nontrivial L-shaped configurations, then it must have density at least
$S$ contains no nontrivial L-shaped configurations, then it must have density at least ![]() $\sigma +\Omega (\sigma ^{O(1)})$ on a set of the form
$\sigma +\Omega (\sigma ^{O(1)})$ on a set of the form
where ![]() $\Phi \subset A\times \mathbb {F}_p^n$ is of the form
$\Phi \subset A\times \mathbb {F}_p^n$ is of the form
for some element ![]() $u\in \mathbb {F}_p^n$ and collection of subspaces
$u\in \mathbb {F}_p^n$ and collection of subspaces ![]() $\{V_x:x\in A\}$ of
$\{V_x:x\in A\}$ of ![]() $\mathbb {F}_p^n$, where
$\mathbb {F}_p^n$, where ![]() $A,B,C,D\subset \mathbb {F}_p^n$ are large and
$A,B,C,D\subset \mathbb {F}_p^n$ are large and ![]() $\operatorname {codim} V_x$ is small for each
$\operatorname {codim} V_x$ is small for each ![]() $x\in A$. Note that this set
$x\in A$. Note that this set ![]() $\Phi$ is not quite as general as the one appearing at the very beginning of this subsection, as the element
$\Phi$ is not quite as general as the one appearing at the very beginning of this subsection, as the element ![]() $u$ of
$u$ of ![]() $\mathbb {F}_p^n$ does not vary with
$\mathbb {F}_p^n$ does not vary with ![]() $x$. It takes some extra work to show that we can guarantee
$x$. It takes some extra work to show that we can guarantee ![]() $\Phi$ to be of this special form, which turns out to be necessary for our density-increment iteration. We say more about this point in § 6.
$\Phi$ to be of this special form, which turns out to be necessary for our density-increment iteration. We say more about this point in § 6.
We would like to continue the density-increment iteration and show that ![]() $S':= T\cap S$, which also lacks L-shaped configurations, has a further density increment of at least the same size as the first on a subset
$S':= T\cap S$, which also lacks L-shaped configurations, has a further density increment of at least the same size as the first on a subset ![]() $T'$ of
$T'$ of ![]() $T$ of the same general form (11). Analogously to Shkredov's argument for corners, we can only hope to do this if
$T$ of the same general form (11). Analogously to Shkredov's argument for corners, we can only hope to do this if ![]() $A,B,C,D,$ and
$A,B,C,D,$ and ![]() $\Phi$ are sufficiently pseudorandom, for some appropriate notions of pseudorandomness. We will need to control the count of L-shaped configurations by the norms
$\Phi$ are sufficiently pseudorandom, for some appropriate notions of pseudorandomness. We will need to control the count of L-shaped configurations by the norms ![]() $\|\cdot \|_{\star _1}$,
$\|\cdot \|_{\star _1}$, ![]() $\|\cdot \|_{\star _2}$, and
$\|\cdot \|_{\star _2}$, and ![]() $\|\cdot \|_{\star _3}$ defined in (8), (9), and (10) with no loss of density factors, i.e. show that
$\|\cdot \|_{\star _3}$ defined in (8), (9), and (10) with no loss of density factors, i.e. show that
and
and also obtain a density increment with no loss of density factors when some localized norm ![]() $\|\cdot \|_{\star _i}$ of the balanced function of a set is large, i.e. show that if
$\|\cdot \|_{\star _i}$ of the balanced function of a set is large, i.e. show that if
where now ![]() $g_S:=S-\sigma T$, then there exists a subset
$g_S:=S-\sigma T$, then there exists a subset ![]() $T'\subset T$ of the same general form,
$T'\subset T$ of the same general form,
as ![]() $T$ on which
$T$ on which ![]() $S$ has a density increment
$S$ has a density increment
depending only on ![]() $\delta$. Such results are needed so that the density increment obtained at each step of the iteration is independent of the step. If one is not sufficiently careful, it is easy to end up with a density increment that gets smaller as the subset
$\delta$. Such results are needed so that the density increment obtained at each step of the iteration is independent of the step. If one is not sufficiently careful, it is easy to end up with a density increment that gets smaller as the subset ![]() $T$ of
$T$ of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ gets sparser, which is not enough to close the density increment iteration.
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ gets sparser, which is not enough to close the density increment iteration.
To carry out these arguments, we will need ![]() $A,B,C,$ and
$A,B,C,$ and ![]() $D$ to be pseudorandom with respect to the
$D$ to be pseudorandom with respect to the ![]() $U^{10}(\mathbb {F}_p^n)$-norm. The situation for
$U^{10}(\mathbb {F}_p^n)$-norm. The situation for ![]() $\Phi$ is more complicated, and deciding on a good measure of pseudorandomness for
$\Phi$ is more complicated, and deciding on a good measure of pseudorandomness for ![]() $\Phi$ that is amenable to a Shkredov-like pseudorandomization procedure and can also be used to analyze the various averages appearing throughout our argument is one of the challenges of the proof of Theorem 1.2. A suitable condition on
$\Phi$ that is amenable to a Shkredov-like pseudorandomization procedure and can also be used to analyze the various averages appearing throughout our argument is one of the challenges of the proof of Theorem 1.2. A suitable condition on ![]() $\Phi$ turns out to be that it is pseudorandom with respect to the
$\Phi$ turns out to be that it is pseudorandom with respect to the ![]() $U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norm. This condition is not, on its own, immediately useful in the arguments of §§ 5 and 6, since the various averages that appear are not controllable by the
$U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norm. This condition is not, on its own, immediately useful in the arguments of §§ 5 and 6, since the various averages that appear are not controllable by the ![]() $U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norm of
$U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norm of ![]() $\Phi$. It takes a bit of work to show that it implies a roughly equivalent statement about the typical codimensions of certain affine subspaces obtained from
$\Phi$. It takes a bit of work to show that it implies a roughly equivalent statement about the typical codimensions of certain affine subspaces obtained from ![]() $\Phi$. We prove this in § 4, deriving some new results on the combinatorics of approximate polynomials along the way.
$\Phi$. We prove this in § 4, deriving some new results on the combinatorics of approximate polynomials along the way.
The proof of the implications (13), (14), and (15) when ![]() $A,B,C,D,$ and
$A,B,C,D,$ and ![]() $\Phi$ are sufficiently pseudorandom consists of many careful applications of the Cauchy–Schwarz inequality, along with appeals to standard facts about the number of linear configurations of bounded Cauchy–Schwarz complexity in products of pseudorandom sets intersected with subspaces of bounded codimension. We carry out this argument in § 5.
$\Phi$ are sufficiently pseudorandom consists of many careful applications of the Cauchy–Schwarz inequality, along with appeals to standard facts about the number of linear configurations of bounded Cauchy–Schwarz complexity in products of pseudorandom sets intersected with subspaces of bounded codimension. We carry out this argument in § 5.
Obtaining a large enough density increment when ![]() $\|g_S\|_{\star _1}$ is large for
$\|g_S\|_{\star _1}$ is large for ![]() $S\subset T$ requires some new ideas and a significant amount of extra work beyond the proof of the non-localized case, in contrast to the situation for the box norm localized to product sets, where the argument is the same as the non-localized case. In order to get such a density increment that only depends on
$S\subset T$ requires some new ideas and a significant amount of extra work beyond the proof of the non-localized case, in contrast to the situation for the box norm localized to product sets, where the argument is the same as the non-localized case. In order to get such a density increment that only depends on ![]() $\delta$ and not on the densities of
$\delta$ and not on the densities of ![]() $A,B,C,D,$ or
$A,B,C,D,$ or ![]() $\Phi$, one of the key ingredients is a density-preserving inverse theorem for the
$\Phi$, one of the key ingredients is a density-preserving inverse theorem for the ![]() $U^2(\Phi (x,\cdot ))$-norms on pseudorandom sets derived from
$U^2(\Phi (x,\cdot ))$-norms on pseudorandom sets derived from ![]() $A,B,C,$ and
$A,B,C,$ and ![]() $D$, which we prove using a version of the transference principle. We carry out this argument in § 6.
$D$, which we prove using a version of the transference principle. We carry out this argument in § 6.
As was the case for corners, the sets ![]() $A',B',C',D',$ and
$A',B',C',D',$ and ![]() $\Phi '$ obtained in the previous paragraph are not guaranteed to be pseudorandom. We must also carry out a pseudorandomizing procedure to locate a product of large affine subspaces of the form
$\Phi '$ obtained in the previous paragraph are not guaranteed to be pseudorandom. We must also carry out a pseudorandomizing procedure to locate a product of large affine subspaces of the form ![]() $(u+V)\times (w+V)$ on which
$(u+V)\times (w+V)$ on which ![]() $A',B',C',D',$ and
$A',B',C',D',$ and ![]() $\Phi '$ are sufficiently pseudorandom and
$\Phi '$ are sufficiently pseudorandom and ![]() $S$ still has a large density increment on
$S$ still has a large density increment on ![]() $T'\cap [(u+V)\times (w+V)]$. Our pseudorandomization procedure is similar to Shkredov's, but with some new complications coming from our desire for
$T'\cap [(u+V)\times (w+V)]$. Our pseudorandomization procedure is similar to Shkredov's, but with some new complications coming from our desire for ![]() $A',B',C',$ and
$A',B',C',$ and ![]() $D'$ and
$D'$ and ![]() $\Phi '$ to be pseudorandom with respect to the
$\Phi '$ to be pseudorandom with respect to the ![]() $U^{10}(\mathbb {F}_p^n)$- and
$U^{10}(\mathbb {F}_p^n)$- and ![]() $U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norms, respectively, and from
$U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norms, respectively, and from ![]() $\Phi '$'s particular structure as a union of affine subspaces in the second factor of
$\Phi '$'s particular structure as a union of affine subspaces in the second factor of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$. To handle the first complication, we use a recent quantitative inverse theorem of Gowers and Milićević [Reference Gowers and MilićevićGM20] for the
$\mathbb {F}_p^n\times \mathbb {F}_p^n$. To handle the first complication, we use a recent quantitative inverse theorem of Gowers and Milićević [Reference Gowers and MilićevićGM20] for the ![]() $U^{s}$-norms on vector spaces over finite fields, combined with a result of Cohen and Tal [Reference Cohen and TalCT15] that allows us to partition
$U^{s}$-norms on vector spaces over finite fields, combined with a result of Cohen and Tal [Reference Cohen and TalCT15] that allows us to partition ![]() $\mathbb {F}_p^n$ into large affine subspaces on which any finite collection of bounded degree polynomials are all constant. The structure of
$\mathbb {F}_p^n$ into large affine subspaces on which any finite collection of bounded degree polynomials are all constant. The structure of ![]() $\Phi '$ has the potential to cause issues in a Shkredov-like pseudorandomization argument, since the intersection of
$\Phi '$ has the potential to cause issues in a Shkredov-like pseudorandomization argument, since the intersection of ![]() $\Phi '$ with a cell may no longer be the union of affine subspaces all having the same dimension. We will explain how this complication is dealt with in § 7, since it requires a bit of set up.
$\Phi '$ with a cell may no longer be the union of affine subspaces all having the same dimension. We will explain how this complication is dealt with in § 7, since it requires a bit of set up.
2.3 Key intermediate results
We finish this section by stating the key intermediate results needed to prove Theorem 1.2 that we just described in the outline. Recall that ![]() $g_S=S-\sigma$ denotes the balanced function of
$g_S=S-\sigma$ denotes the balanced function of ![]() $S$.
$S$.
Lemma 2.3 (Estimation of  $\Lambda (T,T,T,S)$)
$\Lambda (T,T,T,S)$)
There exist absolute constants ![]() $0< c_1<1< c_2$ such that the following holds. Let
$0< c_1<1< c_2$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Define
$d$. Define ![]() $T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11) and suppose that
$T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11) and suppose that ![]() $S\subset T$ has density
$S\subset T$ has density ![]() $\sigma$ in
$\sigma$ in ![]() $T$. Let
$T$. Let ![]() $\varepsilon \leq c_1(\sigma \alpha \beta \gamma \delta \rho )^{c_2}$ and assume that
$\varepsilon \leq c_1(\sigma \alpha \beta \gamma \delta \rho )^{c_2}$ and assume that
Then
As a consequence, we get that if ![]() $\varepsilon$ is small enough,
$\varepsilon$ is small enough, ![]() $n$ is large enough, and
$n$ is large enough, and ![]() $S\subset T$ has no nontrivial L-shaped configurations, then
$S\subset T$ has no nontrivial L-shaped configurations, then
Lemma 2.4 (Control by  $\|\cdot \|_{\star _i}$ norms)
$\|\cdot \|_{\star _i}$ norms)
Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Assume that
$d$. Assume that
Define ![]() $T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11) and suppose that
$T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11) and suppose that ![]() $f_0,f_1,f_2,f_3:\mathbb {F}_p^n\times \mathbb {F}_p^n\to \mathbb {C}$ are
$f_0,f_1,f_2,f_3:\mathbb {F}_p^n\times \mathbb {F}_p^n\to \mathbb {C}$ are ![]() $1$-bounded functions supported on
$1$-bounded functions supported on ![]() $T$. Then
$T$. Then
and
Thus, if ![]() $\varepsilon$ is small enough,
$\varepsilon$ is small enough, ![]() $n$ is large enough, and
$n$ is large enough, and ![]() $S\subset T$ has no nontrivial L-shaped configurations, then one of
$S\subset T$ has no nontrivial L-shaped configurations, then one of
is ![]() $\gg \sigma ^{O(1)}$.
$\gg \sigma ^{O(1)}$.
Theorem 2.5 ( $\|g_S\|_{\star _1}$,
$\|g_S\|_{\star _1}$,  $\|g_S\|_{\star _2}$, or
$\|g_S\|_{\star _2}$, or  $\|g_S\|_{\star _3}$ large implies a density increment)
$\|g_S\|_{\star _3}$ large implies a density increment)
There exist absolute constants ![]() $0< c_1<1< c_2,c_3$ such that the following holds. Let
$0< c_1<1< c_2,c_3$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\sigma,\tau >0$ and
$\sigma,\tau >0$ and
and assume that
Define ![]() $T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11) and assume that
$T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11) and assume that ![]() $S\subset T$ has density
$S\subset T$ has density ![]() $\sigma$ in
$\sigma$ in ![]() $T$. Suppose that
$T$. Suppose that
 \begin{gather*} \|g_S\|_{\star_1}\geq\tau\alpha^{1/4}\beta^{1/2}\gamma\delta\rho^{3/4},\\ \|g_S\|_{\star_2}\geq\tau\alpha^{1/2}\beta\gamma^{1/2}\delta\rho, \end{gather*}
\begin{gather*} \|g_S\|_{\star_1}\geq\tau\alpha^{1/4}\beta^{1/2}\gamma\delta\rho^{3/4},\\ \|g_S\|_{\star_2}\geq\tau\alpha^{1/2}\beta\gamma^{1/2}\delta\rho, \end{gather*}
or
Then, ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\tau ^{O(1)})$ on a subset
$\sigma +\Omega (\tau ^{O(1)})$ on a subset ![]() $T'\subset T$ of the form
$T'\subset T$ of the form
where the densities of ![]() $A',B',C',D'\subset \mathbb {F}_p^n$ are all
$A',B',C',D'\subset \mathbb {F}_p^n$ are all ![]() $\gg (\sigma \tau \alpha \beta \gamma \delta \rho )^{O(1)}$, and the set
$\gg (\sigma \tau \alpha \beta \gamma \delta \rho )^{O(1)}$, and the set ![]() $\Phi '\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi '\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x'$ is a subspace of
$V_x'$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d+1$.
$d+1$.
The first three lemmas combined tell us that if ![]() $S$ has density
$S$ has density ![]() $\sigma$ and contains no nontrivial L-shaped configurations, then one can find a subset
$\sigma$ and contains no nontrivial L-shaped configurations, then one can find a subset ![]() $T$ of
$T$ of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ of the form (11) on which
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ of the form (11) on which ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\sigma ^{O(1)})$. The next lemma tells us that, after restricting to a product of large affine subspaces, we can get this same conclusion with
$\sigma +\Omega (\sigma ^{O(1)})$. The next lemma tells us that, after restricting to a product of large affine subspaces, we can get this same conclusion with ![]() $A,B,C,D,$ and
$A,B,C,D,$ and ![]() $\Phi$ as pseudorandom as we need, which will allow us to continue the density-increment iteration.
$\Phi$ as pseudorandom as we need, which will allow us to continue the density-increment iteration.
Lemma 2.6 There exist absolute constants ![]() $0< c_1<1< c_2,c,c'$ such that the following holds. Let
$0< c_1<1< c_2,c,c'$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Let
$\rho :=p^{-d}$. Let ![]() $\varepsilon '>0$, and suppose that
$\varepsilon '>0$, and suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ and takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ and takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Define
$d$. Define ![]() $T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11), and assume that
$T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ by (11), and assume that ![]() $S\subset T$ has density
$S\subset T$ has density ![]() $\sigma +\tau$ in
$\sigma +\tau$ in ![]() $T$, as well as that
$T$, as well as that
Then there exists a subspace ![]() $V\leq \mathbb {F}_p^n$ of dimension
$V\leq \mathbb {F}_p^n$ of dimension
![]() $u,w\in \mathbb {F}_p^n$, and
$u,w\in \mathbb {F}_p^n$, and ![]() $0\leq i\leq d$ such that, on setting
$0\leq i\leq d$ such that, on setting ![]() $\mathcal {C}=(u+V)\times (w+V)$:
$\mathcal {C}=(u+V)\times (w+V)$:
–
 $B':= B\cap (w+V)$;
$B':= B\cap (w+V)$;–
 $C':=C\cap (u+w+V)$;
$C':=C\cap (u+w+V)$;–
 $D':= D\cap (2u+w+V)$;
$D':= D\cap (2u+w+V)$;–
 $\Psi ':=\Phi \cap \mathcal {C}$ and
$\Psi ':=\Phi \cap \mathcal {C}$ and  $\Phi ':=\{(x,y)\in \Psi ':\mathbb {E}_{z\in w+V}\Psi '(x,z)=p^{-i}\}$;
$\Phi ':=\{(x,y)\in \Psi ':\mathbb {E}_{z\in w+V}\Psi '(x,z)=p^{-i}\}$;–
 $A':=\{x\in u+V:\mathbb {E}_{z\in w+V}\Phi '(x,z)\neq 0\}$;
$A':=\{x\in u+V:\mathbb {E}_{z\in w+V}\Phi '(x,z)\neq 0\}$;–
 $\alpha '=\mu _{u+V}(A')$;
$\alpha '=\mu _{u+V}(A')$;–
 $\beta ':=\mu _{w+V}(B')$;
$\beta ':=\mu _{w+V}(B')$;–
 $\gamma ':=\mu _{u+w+V}(C')$;
$\gamma ':=\mu _{u+w+V}(C')$;–
 $\delta ':=\mu _{2u+w+V}(D')$;
$\delta ':=\mu _{2u+w+V}(D')$;–
 $\rho ':=p^{-i}$; and
$\rho ':=p^{-i}$; and–
 $T':=\{(x,y)\in \mathcal {C}:B'(y)C'(x+y)D'(2x+y)\Phi '(x,y)=1\}$;
$T':=\{(x,y)\in \mathcal {C}:B'(y)C'(x+y)D'(2x+y)\Phi '(x,y)=1\}$;
we have
 \begin{gather*} \|A'-\rho'\|_{U^{10}(u+V)},\quad \|B'-\beta'\|_{U^{10}(w+V)},\quad \|C'-\gamma'\|_{U^{10}(u+w+V)},\quad \|D'-\delta'\|_{U^{10}(2u+w+V)},\\ \|\Phi'-\alpha'\rho'\|_{U^{8}(\mathcal{C})}<2\varepsilon, \end{gather*}
\begin{gather*} \|A'-\rho'\|_{U^{10}(u+V)},\quad \|B'-\beta'\|_{U^{10}(w+V)},\quad \|C'-\gamma'\|_{U^{10}(u+w+V)},\quad \|D'-\delta'\|_{U^{10}(2u+w+V)},\\ \|\Phi'-\alpha'\rho'\|_{U^{8}(\mathcal{C})}<2\varepsilon, \end{gather*}
![]() $\alpha ',\beta ',\gamma ',\delta '\gg \tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/4$, and
$\alpha ',\beta ',\gamma ',\delta '\gg \tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/4$, and
By combining the previous four lemmas and using that L-shaped configurations are preserved by translation and invertible linear transformations of the form ![]() $(x,y)\mapsto (Ex,Ey)$, we thus deduce the following density-increment lemma, which we will iterate in § 8 to prove Theorem 1.2.
$(x,y)\mapsto (Ex,Ey)$, we thus deduce the following density-increment lemma, which we will iterate in § 8 to prove Theorem 1.2.
Lemma 2.7 There exist absolute constants ![]() $0< c_1<1< c_2,c_3,c_4,c,c'$ such that the following holds. Let
$0< c_1<1< c_2,c_3,c_4,c,c'$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Define
$d$. Define ![]() $T$ by (11) and let
$T$ by (11) and let ![]() $S\subset T$ have density
$S\subset T$ have density ![]() $\sigma$ in
$\sigma$ in ![]() $T$. Let
$T$. Let ![]() $\varepsilon \leq (\sigma \alpha \beta \gamma \delta \rho )^{c_2}\exp (-(64/\sigma )^{c_3})$, and assume that
$\varepsilon \leq (\sigma \alpha \beta \gamma \delta \rho )^{c_2}\exp (-(64/\sigma )^{c_3})$, and assume that
Let ![]() $\varepsilon '>0$, and suppose that
$\varepsilon '>0$, and suppose that ![]() $S$ has no nontrivial L-shaped configurations. Then either:
$S$ has no nontrivial L-shaped configurations. Then either:
(i)
 $n<\exp ^2( {c_4\exp ^c(c'/\varepsilon ')}/{(\sigma \alpha \beta \gamma \delta \rho )^{c_2}})$; or
$n<\exp ^2( {c_4\exp ^c(c'/\varepsilon ')}/{(\sigma \alpha \beta \gamma \delta \rho )^{c_2}})$; or(ii) there exists natural numbers
 $n'$ and
$n'$ and  $d'$ satisfying
and
$d'$ satisfying
and \[ n'\gg n^{c_1^{\exp^c(c'/\varepsilon')/(\sigma\alpha\beta\gamma\delta\rho)^{c_2}}} \]
\[ n'\gg n^{c_1^{\exp^c(c'/\varepsilon')/(\sigma\alpha\beta\gamma\delta\rho)^{c_2}}} \]
 $0\leq d'\leq d+1$, subsets
$0\leq d'\leq d+1$, subsets  $A',B',C',D'\subset \mathbb {F}_p^{n'}$ of densities
$A',B',C',D'\subset \mathbb {F}_p^{n'}$ of densities  $\alpha ',\beta ',\gamma ',\delta '$, respectively, a subset
$\alpha ',\beta ',\gamma ',\delta '$, respectively, a subset  $\Phi '\subset \mathbb {F}_p^{n'}\times \mathbb {F}_p^{n'}$ of the form
where each
$\Phi '\subset \mathbb {F}_p^{n'}\times \mathbb {F}_p^{n'}$ of the form
where each \[ \Phi'=\{(x,y)\in A'\times\mathbb{F}_p^{n'}:y\in u'+V_x'\}, \]
\[ \Phi'=\{(x,y)\in A'\times\mathbb{F}_p^{n'}:y\in u'+V_x'\}, \]
 $V_x'$ is a subspace of
$V_x'$ is a subspace of  $\mathbb {F}_p^{n'}$ of codimension
$\mathbb {F}_p^{n'}$ of codimension  $d'$ (so that
$d'$ (so that  $\Phi '$ has density
$\Phi '$ has density  $\alpha '\rho '$, where
$\alpha '\rho '$, where  $\rho ':=p^{-d'}$), and a subset
$\rho ':=p^{-d'}$), and a subset  $S'\subset T'$, where
of density at least
$S'\subset T'$, where
of density at least \[ T':=\{(x,y)\in\mathbb{F}_p^{n'}\times\mathbb{F}_p^{n'}:B'(y)C'(x+y)D'(2x+y)\Phi'(x,y)=1\}, \]
\[ T':=\{(x,y)\in\mathbb{F}_p^{n'}\times\mathbb{F}_p^{n'}:B'(y)C'(x+y)D'(2x+y)\Phi'(x,y)=1\}, \]
 $\sigma +\Omega (\sigma ^{O(1)})$ in
$\sigma +\Omega (\sigma ^{O(1)})$ in  $T'$, such that
$T'$, such that
 \begin{gather*} \|A'-\alpha'\|_{U^{10}(\mathbb{F}_p^{n'})},\quad \|B'-\beta'\|_{U^{10}(\mathbb{F}_p^{n'})},\quad \|C'-\gamma'\|_{U^{10}(\mathbb{F}_p^{n'})},\\ \|D'-\delta'\|_{U^{10}(\mathbb{F}_p^{n'})},\quad \|\Phi'-\alpha'\rho'\|_{U^8(\mathbb{F}_p^{n'}\times\mathbb{F}_p^{n'})}<\varepsilon', \end{gather*}
\begin{gather*} \|A'-\alpha'\|_{U^{10}(\mathbb{F}_p^{n'})},\quad \|B'-\beta'\|_{U^{10}(\mathbb{F}_p^{n'})},\quad \|C'-\gamma'\|_{U^{10}(\mathbb{F}_p^{n'})},\\ \|D'-\delta'\|_{U^{10}(\mathbb{F}_p^{n'})},\quad \|\Phi'-\alpha'\rho'\|_{U^8(\mathbb{F}_p^{n'}\times\mathbb{F}_p^{n'})}<\varepsilon', \end{gather*}
 $\alpha ',\beta ',\gamma ',\delta '\geq (\sigma \alpha \beta \gamma \delta \rho )^{c_2}$, and
$\alpha ',\beta ',\gamma ',\delta '\geq (\sigma \alpha \beta \gamma \delta \rho )^{c_2}$, and  $S'$ contains no nontrivial L-shaped configurations.
$S'$ contains no nontrivial L-shaped configurations.
3. Additional preliminaries
In this section, we present some more preliminaries that were not needed for the outline of the proof of Theorem 1.2, but will be convenient to have for the proof itself. We begin with the notion of Cauchy–Schwarz complexity, first defined by Green and Tao in [Reference Green and TaoGT10].
Definition 3.1 (Cauchy–Schwarz complexity)
Let ![]() $\psi _1,\ldots,\psi _d:(\mathbb {F}_p^n)^r\to \mathbb {F}_p^n$ be a collection of linear forms in
$\psi _1,\ldots,\psi _d:(\mathbb {F}_p^n)^r\to \mathbb {F}_p^n$ be a collection of linear forms in ![]() $r$ variables. We say that
$r$ variables. We say that ![]() $\psi _1,\ldots,\psi _d$ has Cauchy–Schwarz complexity at most
$\psi _1,\ldots,\psi _d$ has Cauchy–Schwarz complexity at most ![]() $s$ if, for every
$s$ if, for every ![]() $j\in [d]$, there exists a partition of
$j\in [d]$, there exists a partition of ![]() $\{\psi _1,\ldots,\psi _d\}\setminus \{\psi _j\}$ into at most
$\{\psi _1,\ldots,\psi _d\}\setminus \{\psi _j\}$ into at most ![]() $s+1$ subsets such that
$s+1$ subsets such that ![]() $\psi _j$ is not contained in the linear span of any of the subsets.
$\psi _j$ is not contained in the linear span of any of the subsets.
The smallest ![]() $s$ such that
$s$ such that ![]() $\{\psi _1,\ldots,\psi _d\}$ has Cauchy–Schwarz complexity at most
$\{\psi _1,\ldots,\psi _d\}$ has Cauchy–Schwarz complexity at most ![]() $s$ is called the Cauchy–Schwarz complexity of
$s$ is called the Cauchy–Schwarz complexity of ![]() $\{\psi _1,\ldots,\psi _d\}$.
$\{\psi _1,\ldots,\psi _d\}$.
For example, four term arithmetic progressions,
have Cauchy–Schwarz complexity ![]() $2$.
$2$.
Any system of linear forms of complexity at most ![]() $s$ can be shown to be controlled by the
$s$ can be shown to be controlled by the ![]() $U^{s+1}$-norm using repeated applications of the Cauchy–Schwarz inequality. In particular, carrying out the proof of the generalized von Neumann theorem of Green and Tao in [Reference Green and TaoGT10] in the finite field model setting (where the technical details are much simpler) produces the following useful result.
$U^{s+1}$-norm using repeated applications of the Cauchy–Schwarz inequality. In particular, carrying out the proof of the generalized von Neumann theorem of Green and Tao in [Reference Green and TaoGT10] in the finite field model setting (where the technical details are much simpler) produces the following useful result.
Theorem 3.2 Let ![]() $\psi _1,\ldots,\psi _d:(\mathbb {F}_p^n)^r\to \mathbb {F}_p^n$ be a collection of linear forms in
$\psi _1,\ldots,\psi _d:(\mathbb {F}_p^n)^r\to \mathbb {F}_p^n$ be a collection of linear forms in ![]() $r$ variables with Cauchy–Schwarz complexity at most
$r$ variables with Cauchy–Schwarz complexity at most ![]() $s$. For any
$s$. For any ![]() $1$-bounded functions
$1$-bounded functions ![]() $f_1,\ldots,f_d:\mathbb {F}_p^n\to \mathbb {C}$, we have
$f_1,\ldots,f_d:\mathbb {F}_p^n\to \mathbb {C}$, we have
 \[ \bigg|\mathbb{E}_{x_1,\ldots,x_r}\prod_{j=1}^df_j(\psi_j(x_1,\ldots,x_r))\bigg|\leq \min_{1\leq j\leq d}\|f_j\|_{U^{s+1}(\mathbb{F}_p^n)}. \]
\[ \bigg|\mathbb{E}_{x_1,\ldots,x_r}\prod_{j=1}^df_j(\psi_j(x_1,\ldots,x_r))\bigg|\leq \min_{1\leq j\leq d}\|f_j\|_{U^{s+1}(\mathbb{F}_p^n)}. \]
Further, if all of ![]() $f_1,\ldots,f_d$ are supported on a set
$f_1,\ldots,f_d$ are supported on a set ![]() $A\subset \mathbb {F}_p^n$ of density
$A\subset \mathbb {F}_p^n$ of density ![]() $\alpha$ that satisfies
$\alpha$ that satisfies ![]() $\|A-\alpha \|_{U^{s+1}(\mathbb {F}_p^n)}<\alpha \varepsilon$, then
$\|A-\alpha \|_{U^{s+1}(\mathbb {F}_p^n)}<\alpha \varepsilon$, then
 \[ \bigg|\mathbb{E}_{x_1,\ldots,x_r}\prod_{j=1}^df_j(\psi_j(x_1,\ldots,x_r))\bigg|\leq \alpha^{d-1}\min_{1\leq j\leq d}\|f_j\|_{U^{s+1}(\mathbb{F}_p^n)}+O_{d,s}(\varepsilon^{\Omega_{d,s}(1)}). \]
\[ \bigg|\mathbb{E}_{x_1,\ldots,x_r}\prod_{j=1}^df_j(\psi_j(x_1,\ldots,x_r))\bigg|\leq \alpha^{d-1}\min_{1\leq j\leq d}\|f_j\|_{U^{s+1}(\mathbb{F}_p^n)}+O_{d,s}(\varepsilon^{\Omega_{d,s}(1)}). \]
We will use the following immediate corollary of Theorem 3.2 numerous times throughout the proof of Theorem 1.2.
Corollary 3.3 Let ![]() $\psi _1,\ldots,\psi _d:(\mathbb {F}_p^n)^r\to \mathbb {F}_p^n$ be a collection of linear forms in
$\psi _1,\ldots,\psi _d:(\mathbb {F}_p^n)^r\to \mathbb {F}_p^n$ be a collection of linear forms in ![]() $r$ variables with Cauchy–Schwarz complexity at most
$r$ variables with Cauchy–Schwarz complexity at most ![]() $s$. Suppose that
$s$. Suppose that ![]() $f_1,\ldots,f_d:\mathbb {F}_p^n\to \mathbb {C}$ are
$f_1,\ldots,f_d:\mathbb {F}_p^n\to \mathbb {C}$ are ![]() $1$-bounded functions having average values
$1$-bounded functions having average values ![]() $\alpha _1,\ldots,\alpha _d$, respectively, and that
$\alpha _1,\ldots,\alpha _d$, respectively, and that
for all ![]() $1\leq j\leq d$. Then
$1\leq j\leq d$. Then
 \[ \bigg|\mathbb{E}_{x_1,\ldots,x_r}\prod_{j=1}^df_j(\psi_j(x_1,\ldots,x_r))-\prod_{j=1}^d\alpha_j\bigg|\leq d\max_{1\leq j\leq d}\varepsilon_j. \]
\[ \bigg|\mathbb{E}_{x_1,\ldots,x_r}\prod_{j=1}^df_j(\psi_j(x_1,\ldots,x_r))-\prod_{j=1}^d\alpha_j\bigg|\leq d\max_{1\leq j\leq d}\varepsilon_j. \]
We also need the Gowers–Cauchy–Schwarz inequality.
Lemma 3.4 (Gowers–Cauchy–Schwarz inequality)
Let ![]() $s$ be a natural number,
$s$ be a natural number, ![]() $H$ be an abelian group, and
$H$ be an abelian group, and ![]() $f_\omega :H\to \mathbb {C}$ for every
$f_\omega :H\to \mathbb {C}$ for every ![]() $\omega \in \{0,1\}^s$. We have
$\omega \in \{0,1\}^s$. We have
 \[ \bigg|\mathbb{E}_{x,h_1,\ldots,h_s\in H}\prod_{\omega\in\{0,1\}^s}f_\omega (x+\omega\cdot(h_1,\ldots,h_s))\bigg|\leq\prod_{\omega\in\{0,1\}^s}\|f_\omega\|_{U^s(H)}. \]
\[ \bigg|\mathbb{E}_{x,h_1,\ldots,h_s\in H}\prod_{\omega\in\{0,1\}^s}f_\omega (x+\omega\cdot(h_1,\ldots,h_s))\bigg|\leq\prod_{\omega\in\{0,1\}^s}\|f_\omega\|_{U^s(H)}. \]
Next, we record the basic fact that a function on ![]() $\mathbb {F}_p^n$ with small
$\mathbb {F}_p^n$ with small ![]() $U^2$-norm has small average on affine subspaces of small codimension.
$U^2$-norm has small average on affine subspaces of small codimension.
Lemma 3.5 Let ![]() $f:\mathbb {F}_p^n\to \mathbb {C}$ be a
$f:\mathbb {F}_p^n\to \mathbb {C}$ be a ![]() $1$-bounded function satisfying
$1$-bounded function satisfying ![]() $\|f\|_{U^2(\mathbb {F}_p^n)}<\varepsilon$ and
$\|f\|_{U^2(\mathbb {F}_p^n)}<\varepsilon$ and ![]() $w+V\subset \mathbb {F}_p^n$ be an affine subspace of codimension
$w+V\subset \mathbb {F}_p^n$ be an affine subspace of codimension ![]() $d$. Then
$d$. Then
Proof. The indicator function of ![]() $V$ can be written as
$V$ can be written as
 \[ \frac{1}{p^d}\sum_{\xi\in V^\perp}e_p(\xi\cdot x), \]
\[ \frac{1}{p^d}\sum_{\xi\in V^\perp}e_p(\xi\cdot x), \]
so we have that
 \[ |\mathbb{E}_{x}f(x-w)V(x)|\leq\frac{1}{p^d}\sum_{\xi\in V^\perp} |\mathbb{E}_{x}f(x)e_p(\xi\cdot x)|\leq \|f\|_{U^2(\mathbb{F}_p^n)}, \]
\[ |\mathbb{E}_{x}f(x-w)V(x)|\leq\frac{1}{p^d}\sum_{\xi\in V^\perp} |\mathbb{E}_{x}f(x)e_p(\xi\cdot x)|\leq \|f\|_{U^2(\mathbb{F}_p^n)}, \]
by the Gowers–Cauchy–Schwarz inequality. Since ![]() $|V|=|\mathbb {F}_p^n|/p^d$, the desired result follows.
$|V|=|\mathbb {F}_p^n|/p^d$, the desired result follows.
The last lemma of this section will be used to analyze the various averages appearing in the proofs of Lemmas 2.3, 2.4, and 2.5.
Lemma 3.6 Let ![]() $\psi _1,\ldots,\psi _d\in \mathbb {F}_p[x_1,\ldots,x_t,y]$ be a collection of linear forms such that the coefficient of
$\psi _1,\ldots,\psi _d\in \mathbb {F}_p[x_1,\ldots,x_t,y]$ be a collection of linear forms such that the coefficient of ![]() $y$ in each of
$y$ in each of ![]() $\psi _1,\ldots,\psi _d$ is nonzero, and
$\psi _1,\ldots,\psi _d$ is nonzero, and ![]() $F:(\mathbb {F}_p^n)^t\times \mathbb {F}_p^n\to [0,1]$ be a function of the form
$F:(\mathbb {F}_p^n)^t\times \mathbb {F}_p^n\to [0,1]$ be a function of the form
 \[ F(\mathbf{x},y)=\prod_{j=1}^df_j(\psi_j(\mathbf{x},y)) \]
\[ F(\mathbf{x},y)=\prod_{j=1}^df_j(\psi_j(\mathbf{x},y)) \]
for some ![]() $1$-bounded functions
$1$-bounded functions ![]() $f_j:\mathbb {F}_p^n\to \mathbb {C}$ with average value
$f_j:\mathbb {F}_p^n\to \mathbb {C}$ with average value ![]() $\beta _j$, each satisfying
$\beta _j$, each satisfying ![]() $\|f_j-\beta _j\|_{U^s(\mathbb {F}_p^n)}<\varepsilon$. If the Cauchy–Schwarz complexity of the set of linear forms
$\|f_j-\beta _j\|_{U^s(\mathbb {F}_p^n)}<\varepsilon$. If the Cauchy–Schwarz complexity of the set of linear forms
 \begin{equation} \bigcup_{j=1}^d\{\psi_j(\mathbf{x},y),\psi_j(\mathbf{x},y+h), \psi_j(\mathbf{x},y+k),\psi_j(\mathbf{x},y+h+k)\} \end{equation}
\begin{equation} \bigcup_{j=1}^d\{\psi_j(\mathbf{x},y),\psi_j(\mathbf{x},y+h), \psi_j(\mathbf{x},y+k),\psi_j(\mathbf{x},y+h+k)\} \end{equation}
in the variables ![]() $x_1,\ldots,x_t,y,h,k$, is at most
$x_1,\ldots,x_t,y,h,k$, is at most ![]() $s-1$, then
$s-1$, then
 \[ \mathbb{P}\bigg(\mathbf{x}\in (\mathbb{F}_p^n)^t:\bigg\|F(\mathbf{x},\cdot)-\prod_{j=1}^d\beta_j\bigg\|_{U^2(\mathbb{F}_p^n)} \geq\varepsilon^{1/8}\bigg)\ll_{d}\sqrt{\varepsilon}. \]
\[ \mathbb{P}\bigg(\mathbf{x}\in (\mathbb{F}_p^n)^t:\bigg\|F(\mathbf{x},\cdot)-\prod_{j=1}^d\beta_j\bigg\|_{U^2(\mathbb{F}_p^n)} \geq\varepsilon^{1/8}\bigg)\ll_{d}\sqrt{\varepsilon}. \]
Proof. Set ![]() $\beta :=\prod _{j=1}^d\beta _j$. Note that
$\beta :=\prod _{j=1}^d\beta _j$. Note that ![]() $\mathbb {E}_{\mathbf {x}\in (\mathbb {F}_p^n)^t}\|F(\mathbf {x},\cdot )-\beta \|_{U^2(\mathbb {F}_p^n)}^4$ equals
$\mathbb {E}_{\mathbf {x}\in (\mathbb {F}_p^n)^t}\|F(\mathbf {x},\cdot )-\beta \|_{U^2(\mathbb {F}_p^n)}^4$ equals
where
 \[ f_i^{\omega}(\mathbf{x},y)=\begin{cases} 1 & \omega_i=1 \\ F(\mathbf{x},y) & \omega_i=0 \end{cases} \]
\[ f_i^{\omega}(\mathbf{x},y)=\begin{cases} 1 & \omega_i=1 \\ F(\mathbf{x},y) & \omega_i=0 \end{cases} \]
for each ![]() $\omega \in \{0,1\}^4$ and
$\omega \in \{0,1\}^4$ and ![]() $1\leq i\leq 4$. Since (19) has Cauchy–Schwarz complexity at most
$1\leq i\leq 4$. Since (19) has Cauchy–Schwarz complexity at most ![]() $s-1$ by hypothesis, Corollary 3.3 implies that
$s-1$ by hypothesis, Corollary 3.3 implies that
for every ![]() $\omega \in \{0,1\}^4$. Thus,
$\omega \in \{0,1\}^4$. Thus,
Markov's inequality then gives
for every ![]() $r>0$. Taking
$r>0$. Taking ![]() $r=\varepsilon ^{1/8}$ gives the conclusion of the lemma.
$r=\varepsilon ^{1/8}$ gives the conclusion of the lemma.
4. Pseudorandomness of  $\Phi$
$\Phi$
The main purpose of this section is to show that if ![]() $\|\Phi -\alpha \rho \|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}$ is small and
$\|\Phi -\alpha \rho \|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}$ is small and ![]() $\Phi$ is a subset of the form
$\Phi$ is a subset of the form
where each ![]() $V_x\leq \mathbf {F}_p^n$ is a subspace of density
$V_x\leq \mathbf {F}_p^n$ is a subspace of density ![]() $\rho$ in
$\rho$ in ![]() $\mathbf {F}_p^n$ and
$\mathbf {F}_p^n$ and ![]() $A\subset \mathbf {F}_p^n$ has density
$A\subset \mathbf {F}_p^n$ has density ![]() $\alpha$ in
$\alpha$ in ![]() $\mathbf {F}_p^n$, then, whenever
$\mathbf {F}_p^n$, then, whenever ![]() $\psi _1,\ldots,\psi _r\in \mathbb {F}_p[x_1,\ldots,x_m]$ is a collection of linear forms of Cauchy–Schwarz complexity at most
$\psi _1,\ldots,\psi _r\in \mathbb {F}_p[x_1,\ldots,x_m]$ is a collection of linear forms of Cauchy–Schwarz complexity at most ![]() $s$ and
$s$ and ![]() $w_1,\ldots,w_r\in \mathbb {F}_p^n$, the affine subspaces
$w_1,\ldots,w_r\in \mathbb {F}_p^n$, the affine subspaces
 \[ \bigg\{y\in \mathbb{F}_p^n:\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)=1\bigg\} \]
\[ \bigg\{y\in \mathbb{F}_p^n:\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)=1\bigg\} \]
typically have maximum possible codimension. This allows us to transform the condition that ![]() $\Phi$ is
$\Phi$ is ![]() $U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-pseudorandom into a more useful property for evaluating the various averages that arise in the proof of Theorem 1.2.
$U^{8}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-pseudorandom into a more useful property for evaluating the various averages that arise in the proof of Theorem 1.2.
Lemma 4.1 For each nonnegative integer ![]() $s$ and positive integer
$s$ and positive integer ![]() $r$, there exist constants
$r$, there exist constants ![]() $C_{s,r},c_{s,r}>0$ such that the following holds. Let
$C_{s,r},c_{s,r}>0$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Let
$\rho :=p^{-d}$. Let ![]() $\delta >0$,
$\delta >0$, ![]() $A\subset \mathbb {F}_p^n$ have density
$A\subset \mathbb {F}_p^n$ have density ![]() $\alpha$, and
$\alpha$, and ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be a set of the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be a set of the form
where each ![]() $V_x\leq \mathbb {F}_p^n$ is a subspace of codimension
$V_x\leq \mathbb {F}_p^n$ is a subspace of codimension ![]() $d$. Assume that
$d$. Assume that
Let ![]() $\psi _1,\ldots,\psi _r\in \mathbb {F}_p[x_1,\ldots,x_m]$ be a collection of linear forms of Cauchy–Schwarz complexity at most
$\psi _1,\ldots,\psi _r\in \mathbb {F}_p[x_1,\ldots,x_m]$ be a collection of linear forms of Cauchy–Schwarz complexity at most ![]() $s$. Then, for all but at most a
$s$. Then, for all but at most a ![]() $\delta$-proportion of
$\delta$-proportion of ![]() $m$-tuples
$m$-tuples ![]() $\mathbf {x}\in (\mathbb {F}_p^{n})^m$ for which
$\mathbf {x}\in (\mathbb {F}_p^{n})^m$ for which ![]() $\psi _1(\mathbf {x}),\ldots,\psi _r(\mathbf {x})\in A$, we must have that
$\psi _1(\mathbf {x}),\ldots,\psi _r(\mathbf {x})\in A$, we must have that
 \[ \operatorname{codim}{\bigg\{y\in \mathbb{F}_p^n:\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)=1\bigg\}}= rd \]
\[ \operatorname{codim}{\bigg\{y\in \mathbb{F}_p^n:\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)=1\bigg\}}= rd \]
for all ![]() $w_1,\ldots,w_r\in \mathbb {F}_p^n$.
$w_1,\ldots,w_r\in \mathbb {F}_p^n$.
We begin by showing that if ![]() $\Phi$ is pseudorandom with respect to the
$\Phi$ is pseudorandom with respect to the ![]() $U^{s}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norm, then
$U^{s}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-norm, then ![]() $A$ is pseudorandom with respect to the
$A$ is pseudorandom with respect to the ![]() $U^{s}(\mathbb {F}_p^n)$-norm. This result will also be useful at a few other points in the proof of Theorem 1.2.
$U^{s}(\mathbb {F}_p^n)$-norm. This result will also be useful at a few other points in the proof of Theorem 1.2.
Lemma 4.2 Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Let
$\rho :=p^{-d}$. Let ![]() $A\subset \mathbb {F}_p^n$ have density
$A\subset \mathbb {F}_p^n$ have density ![]() $\alpha$ and
$\alpha$ and ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be of the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be of the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Then, for every natural number
$d$. Then, for every natural number ![]() $s$, we have
$s$, we have
Proof. We write
and then, for each ![]() $\omega \in \{0,1\}^s$, insert the identity
$\omega \in \{0,1\}^s$, insert the identity
to get that ![]() $\|A-\alpha \|_{U^s(\mathbb {F}_p^n)}^{2^s}$ equals
$\|A-\alpha \|_{U^s(\mathbb {F}_p^n)}^{2^s}$ equals
 \[ \frac{1}{\rho^{2^s}}\mathbb{E}_{x,h_1,\ldots,h_s}\mathbb{E}_{\substack{k_\omega\in\mathbb{F}_p^n \\ \omega\in\{0,1\}^s}}\prod_{\omega\in\{0,1\}^s}(\Phi-\alpha\rho)(x+\omega\cdot(h_1,\ldots,h_s),k_\omega). \]
\[ \frac{1}{\rho^{2^s}}\mathbb{E}_{x,h_1,\ldots,h_s}\mathbb{E}_{\substack{k_\omega\in\mathbb{F}_p^n \\ \omega\in\{0,1\}^s}}\prod_{\omega\in\{0,1\}^s}(\Phi-\alpha\rho)(x+\omega\cdot(h_1,\ldots,h_s),k_\omega). \]
We can average the above quantity over ![]() $y,\ell _1,\ldots,\ell _s$ and make the change of variables
$y,\ell _1,\ldots,\ell _s$ and make the change of variables ![]() $k_\omega \mapsto k_\omega +y+\omega \cdot (\ell _1,\ldots,\ell _s)$ to get that it equals
$k_\omega \mapsto k_\omega +y+\omega \cdot (\ell _1,\ldots,\ell _s)$ to get that it equals
 \begin{equation} \frac{1}{\rho^{2^s}}\mathbb{E}_{\substack{k_\omega\in\mathbb{F}_p^n \\ \omega\in\{0,1\}^s}}\mathbb{E}_{x,y,h_1,\ldots,h_s,\ell_1,\ldots,\ell_s} \prod_{\omega\in\{0,1\}^s}(\Phi-\alpha\rho)((x,k_\omega+y)+ \omega\cdot((h_1,\ell_1),\ldots,(h_s,\ell_s))). \end{equation}
\begin{equation} \frac{1}{\rho^{2^s}}\mathbb{E}_{\substack{k_\omega\in\mathbb{F}_p^n \\ \omega\in\{0,1\}^s}}\mathbb{E}_{x,y,h_1,\ldots,h_s,\ell_1,\ldots,\ell_s} \prod_{\omega\in\{0,1\}^s}(\Phi-\alpha\rho)((x,k_\omega+y)+ \omega\cdot((h_1,\ell_1),\ldots,(h_s,\ell_s))). \end{equation}Applying the Gowers–Cauchy–Schwarz inequality bounds (20) above by
 \[ \frac{1}{\rho^{2^s}}\mathbb{E}_{\substack{k_\omega\in\mathbb{F}_p^n \\ \omega\in\{0,1\}^s}}\prod_{\omega\in\{0,1\}^s}\|(\Phi-\alpha\rho) (\cdot,k_\omega+\cdot)\|_{U^{s}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}= \frac{1}{\rho^{2^s}}\|\Phi-\alpha\rho\|^{2^s}_{U^{s}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}, \]
\[ \frac{1}{\rho^{2^s}}\mathbb{E}_{\substack{k_\omega\in\mathbb{F}_p^n \\ \omega\in\{0,1\}^s}}\prod_{\omega\in\{0,1\}^s}\|(\Phi-\alpha\rho) (\cdot,k_\omega+\cdot)\|_{U^{s}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}= \frac{1}{\rho^{2^s}}\|\Phi-\alpha\rho\|^{2^s}_{U^{s}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}, \]
which gives us the conclusion of the lemma.
To prove Lemma 4.1, we will need the notion of an approximate polynomial of bounded degree, which we define using the additive discrete difference operator ![]() $\partial$. For
$\partial$. For ![]() $\phi :H\to H$ and
$\phi :H\to H$ and ![]() $h\in H$, define
$h\in H$, define ![]() $\partial _h\phi :H\to H$ by
$\partial _h\phi :H\to H$ by
and, for ![]() $h_1,\ldots,h_s\in H$, the
$h_1,\ldots,h_s\in H$, the ![]() $s$-fold additive difference operator
$s$-fold additive difference operator ![]() $\partial _{h_1,\ldots,h_s}$ by
$\partial _{h_1,\ldots,h_s}$ by
Definition 4.3 Let ![]() $H$ be an abelian group,
$H$ be an abelian group, ![]() $A\subset H$, and
$A\subset H$, and ![]() $\phi :A\to H$. We say that
$\phi :A\to H$. We say that ![]() $\phi$ is an
$\phi$ is an ![]() $\varepsilon$-approximate polynomial of degree at most
$\varepsilon$-approximate polynomial of degree at most ![]() $s-1$ on
$s-1$ on ![]() $A$ if
$A$ if
for at least an ![]() $\varepsilon$-proportion of
$\varepsilon$-proportion of ![]() $(s+1)$-tuples
$(s+1)$-tuples ![]() $(x,h_1,\ldots,h_s)\in H^{s+1}$ for which
$(x,h_1,\ldots,h_s)\in H^{s+1}$ for which ![]() $x+\omega \cdot (h_1,\ldots,h_s)\in A$ for all
$x+\omega \cdot (h_1,\ldots,h_s)\in A$ for all ![]() $\omega \in \{0,1\}^s$.
$\omega \in \{0,1\}^s$.
We will also need the following result, which is the key combinatorial input into the proof of Lemma 4.1.
Lemma 4.4 For each nonnegative integer ![]() $s$, there exist constants
$s$, there exist constants ![]() $C_s,c_s>0$ such that the following holds. Let
$C_s,c_s>0$ such that the following holds. Let ![]() $A\subset \mathbb {F}_p^n$ have density
$A\subset \mathbb {F}_p^n$ have density ![]() $\alpha$, with
$\alpha$, with
and ![]() $\phi : A\to \mathbb {F}_p^n$ be a
$\phi : A\to \mathbb {F}_p^n$ be a ![]() $\delta$-approximate polynomial of degree at most
$\delta$-approximate polynomial of degree at most ![]() $s$ on
$s$ on ![]() $A$. Then, for at least a
$A$. Then, for at least a ![]() $\Omega _s(\delta ^{O_s(1)})$-proportion of
$\Omega _s(\delta ^{O_s(1)})$-proportion of ![]() $(2s+2)$-dimensional parallelopipeds
$(2s+2)$-dimensional parallelopipeds
in ![]() $A^{2^{2s+2}}$, the derivative of
$A^{2^{2s+2}}$, the derivative of ![]() $\phi$ on the
$\phi$ on the ![]() $(2s+1)$-dimensional face
$(2s+1)$-dimensional face ![]() $(x+\omega \cdot (h_1,\ldots,h_{2s+2}))_{\substack {\omega \in \{0,1\}^{2s+2} \\ \omega _i=\epsilon }}$,
$(x+\omega \cdot (h_1,\ldots,h_{2s+2}))_{\substack {\omega \in \{0,1\}^{2s+2} \\ \omega _i=\epsilon }}$,
 \[ \sum_{\substack{\omega\in\{0,1\}^{2s+2} \\ \omega_{i}=\epsilon}}(-1)^{|\omega|}\phi(x+\omega\cdot(h_1,\ldots,h_{2s+2})), \]
\[ \sum_{\substack{\omega\in\{0,1\}^{2s+2} \\ \omega_{i}=\epsilon}}(-1)^{|\omega|}\phi(x+\omega\cdot(h_1,\ldots,h_{2s+2})), \]
vanishes for all ![]() $1\leq i\leq 2s+2$ and
$1\leq i\leq 2s+2$ and ![]() $\epsilon =0,1$.
$\epsilon =0,1$.
Proof. We proceed by induction on ![]() $s$, beginning with the case
$s$, beginning with the case ![]() $s=0$. If
$s=0$. If ![]() $\phi$ is a
$\phi$ is a ![]() $\delta$-approximate polynomial of degree at most
$\delta$-approximate polynomial of degree at most ![]() $0$ on
$0$ on ![]() $A$, then
$A$, then ![]() $\mathbb {E}_{x,y\in A}1_{\phi (x)=\phi (y)}\geq \delta$, so that, by the pigeonhole principle, there exists some
$\mathbb {E}_{x,y\in A}1_{\phi (x)=\phi (y)}\geq \delta$, so that, by the pigeonhole principle, there exists some ![]() $z\in \mathbb {F}_p^n$ for which
$z\in \mathbb {F}_p^n$ for which ![]() $\mu _{A}(\{x\in A:\phi (x)=z\})\geq \delta$. Set
$\mu _{A}(\{x\in A:\phi (x)=z\})\geq \delta$. Set ![]() $X:=\{x\in A:\phi (x)=z\}$, and consider the set of quadruples
$X:=\{x\in A:\phi (x)=z\}$, and consider the set of quadruples
Note that if ![]() $(x,x+h,x+k,x+h+k)\in X'$, then
$(x,x+h,x+k,x+h+k)\in X'$, then
so certainly the derivatives
of ![]() $\phi$ on each of the
$\phi$ on each of the ![]() $1$-dimensional faces of the parallelopiped
$1$-dimensional faces of the parallelopiped ![]() $(x,x+h,x+k,x+h+k)$ vanish. Since
$(x,x+h,x+k,x+h+k)$ vanish. Since
 \[ \alpha\delta\leq\|X\|_{U^1(\mathbb{F}_p^n)}\leq\|X\|_{U^2(\mathbb{F}_p^n)}=\bigg(\frac{|X'|}{p^{3n}}\bigg)^{1/4}, \]
\[ \alpha\delta\leq\|X\|_{U^1(\mathbb{F}_p^n)}\leq\|X\|_{U^2(\mathbb{F}_p^n)}=\bigg(\frac{|X'|}{p^{3n}}\bigg)^{1/4}, \]
we must have ![]() $|X'|\geq (\alpha \delta )^4p^{3n}$. Taking
$|X'|\geq (\alpha \delta )^4p^{3n}$. Taking ![]() $c_0=8$, the total number of quadruples
$c_0=8$, the total number of quadruples ![]() $(x,x+h,x+k,x+h+k)$ in
$(x,x+h,x+k,x+h+k)$ in ![]() $A^4$ is
$A^4$ is ![]() $(\alpha ^4+O(C_0\alpha ^8))p^{3n}$ by Corollary 3.3, which means that
$(\alpha ^4+O(C_0\alpha ^8))p^{3n}$ by Corollary 3.3, which means that ![]() $X'$ consists of at least a
$X'$ consists of at least a ![]() $\delta ^4/2$-proportion of parallelograms
$\delta ^4/2$-proportion of parallelograms ![]() $(x,x+h,x+k,x+h+k)$ in
$(x,x+h,x+k,x+h+k)$ in ![]() $A^4$ if
$A^4$ if ![]() $C_0$ is chosen small enough. Thus, for at least a
$C_0$ is chosen small enough. Thus, for at least a ![]() $\delta ^4/2$-proportion of parallelograms
$\delta ^4/2$-proportion of parallelograms ![]() $(x,x+h,x+k,x+h+k)$ in
$(x,x+h,x+k,x+h+k)$ in ![]() $A^4$, the derivative of
$A^4$, the derivative of ![]() $\phi$ on each
$\phi$ on each ![]() $1$-dimensional face vanishes, as desired.
$1$-dimensional face vanishes, as desired.
Now suppose that the result holds for a general degree ![]() $s-1\geq 0$, and let
$s-1\geq 0$, and let ![]() $\phi$ be a
$\phi$ be a ![]() $\delta$-approximate polynomial of degree at most
$\delta$-approximate polynomial of degree at most ![]() $s$ on
$s$ on ![]() $A$. By Corollary 3.3,
$A$. By Corollary 3.3,
so that, as long as ![]() $C_s$ is sufficiently small and
$C_s$ is sufficiently small and ![]() $c_s$ is sufficiently large, it follows from Markov's inequality that
$c_s$ is sufficiently large, it follows from Markov's inequality that
and, thus,
as well, for all but a ![]() $O(\delta ^2)$-proportion of
$O(\delta ^2)$-proportion of ![]() $h\in \mathbb {F}_p^n$. Thus, for at least a
$h\in \mathbb {F}_p^n$. Thus, for at least a ![]() $\Omega (\delta )$-proportion of
$\Omega (\delta )$-proportion of ![]() $h_{s+1}\in \mathbb {F}_p^n$, we have
$h_{s+1}\in \mathbb {F}_p^n$, we have ![]() $\|\Delta _{h_{s+1}}A-\alpha ^2\|_{U^{2s}(\mathbb {F}_p^n)}< C_{s-1}(\alpha \delta /2)^{2c_{s-1}}/2$,
$\|\Delta _{h_{s+1}}A-\alpha ^2\|_{U^{2s}(\mathbb {F}_p^n)}< C_{s-1}(\alpha \delta /2)^{2c_{s-1}}/2$, ![]() $|\mu _{\mathbb {F}_p^n}(A\cap (A-h_{s+1}))-\alpha ^2|< C_{s-1}(\alpha \delta /2)^{2c_{s-1}}/2$, and that the function
$|\mu _{\mathbb {F}_p^n}(A\cap (A-h_{s+1}))-\alpha ^2|< C_{s-1}(\alpha \delta /2)^{2c_{s-1}}/2$, and that the function ![]() $\partial _{h_{s+1}}\phi$ is a
$\partial _{h_{s+1}}\phi$ is a ![]() $O(\delta )$-approximate polynomial of degree at most
$O(\delta )$-approximate polynomial of degree at most ![]() $s-1$ on
$s-1$ on ![]() $A\cap (A-h_{s+1})$. Denoting the set of such
$A\cap (A-h_{s+1})$. Denoting the set of such ![]() $h_{s+1}$ by
$h_{s+1}$ by ![]() $H$, so that
$H$, so that ![]() $\mu _{\mathbb {F}_p^n}(H)\gg \delta$, the induction hypothesis then says that, for each
$\mu _{\mathbb {F}_p^n}(H)\gg \delta$, the induction hypothesis then says that, for each ![]() $h\in H$, there are at least a
$h\in H$, there are at least a ![]() $\Omega _{s}(\delta ^{O_{s}(1)})$-proportion of
$\Omega _{s}(\delta ^{O_{s}(1)})$-proportion of ![]() $2s$-dimensional parallelopipeds
$2s$-dimensional parallelopipeds ![]() $(x+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ in
$(x+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ in ![]() $(A\cap (A-h))^{2^{2s}}$ for which the derivative of
$(A\cap (A-h))^{2^{2s}}$ for which the derivative of ![]() $\partial _h\phi$ on each
$\partial _h\phi$ on each ![]() $(2s-1)$-dimensional face vanishes.
$(2s-1)$-dimensional face vanishes.
Summing over all ![]() $h\in H$, it follows that, for at least a
$h\in H$, it follows that, for at least a ![]() $\Omega _{s}(\delta ^{O_s(1)})$-proportion of
$\Omega _{s}(\delta ^{O_s(1)})$-proportion of ![]() $(2s+2)$-tuples
$(2s+2)$-tuples ![]() $(x,y,h_1,\ldots,h_{2s})$ for which
$(x,y,h_1,\ldots,h_{2s})$ for which ![]() $(x+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ and
$(x+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ and ![]() $(y+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ are both in
$(y+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ are both in ![]() $A^{2^{2s}}$, one has
$A^{2^{2s}}$, one has
for all ![]() $i=1,\ldots,2s$ and
$i=1,\ldots,2s$ and ![]() $\epsilon =0,1$. By Corollary 3.3,
$\epsilon =0,1$. By Corollary 3.3,
and so, by Markov's inequality,
 \begin{equation} \mu_{\mathbb{F}_p^n}\bigg(\bigcap_{\omega\in\{0,1\}^{2s}} [A-\omega\cdot(h_1,\ldots,h_{2s})]\bigg)=\alpha^{2^{2s}}+O([C_s(\alpha\delta)^{c_s}]^{\Omega(1)}) \end{equation}
\begin{equation} \mu_{\mathbb{F}_p^n}\bigg(\bigcap_{\omega\in\{0,1\}^{2s}} [A-\omega\cdot(h_1,\ldots,h_{2s})]\bigg)=\alpha^{2^{2s}}+O([C_s(\alpha\delta)^{c_s}]^{\Omega(1)}) \end{equation}
for all but a ![]() $O([C_s(\alpha \delta )^{c_{s}}]^{\Omega (1)})$-proportion of
$O([C_s(\alpha \delta )^{c_{s}}]^{\Omega (1)})$-proportion of ![]() $(h_1,\ldots,h_{2s})$ in
$(h_1,\ldots,h_{2s})$ in ![]() $(\mathbb {F}_p^n)^{2s}$. By taking
$(\mathbb {F}_p^n)^{2s}$. By taking ![]() $C_s$ small enough and
$C_s$ small enough and ![]() $c_s$ large enough, there are therefore at least a
$c_s$ large enough, there are therefore at least a ![]() $\Omega _{s}(\delta ^{O_s(1)})$-proportion of
$\Omega _{s}(\delta ^{O_s(1)})$-proportion of ![]() $2s$-tuples
$2s$-tuples ![]() $(h_1,\ldots,h_{2s})$ in
$(h_1,\ldots,h_{2s})$ in ![]() $(\mathbb {F}_p^n)^{2s}$ for which (21) holds and, for at least a
$(\mathbb {F}_p^n)^{2s}$ for which (21) holds and, for at least a ![]() $\Omega _{s}(\delta ^{O_s(1)})$-proportion of pairs
$\Omega _{s}(\delta ^{O_s(1)})$-proportion of pairs ![]() $(x,y)\in A^2$ such that
$(x,y)\in A^2$ such that ![]() $(x+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ and
$(x+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ and ![]() $(y+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ are both in
$(y+\omega \cdot (h_1,\ldots,h_{2s}))_{\omega \in \{0,1\}^{2s}}$ are both in ![]() $A^{2^{2s}}$, one also has
$A^{2^{2s}}$, one also has
for all ![]() $i=1,\ldots,2s$ and
$i=1,\ldots,2s$ and ![]() $\epsilon =0,1$. For each such
$\epsilon =0,1$. For each such ![]() $2s$-tuple
$2s$-tuple ![]() $\mathbf {h}$, it follows from the pigeonhole principle that there exists a
$\mathbf {h}$, it follows from the pigeonhole principle that there exists a ![]() $y_{\mathbf {h}}$ in the set
$y_{\mathbf {h}}$ in the set
such that, for at least a ![]() $\Omega _{s}(\delta ^{O_s(1)})$-proportion of
$\Omega _{s}(\delta ^{O_s(1)})$-proportion of ![]() $x\in A_{\mathbf {h}}$, one has
$x\in A_{\mathbf {h}}$, one has
for all ![]() $i=1,\ldots,2s$ and
$i=1,\ldots,2s$ and ![]() $\epsilon =0,1$.
$\epsilon =0,1$.
Now set ![]() $v_{i,\epsilon,\mathbf {h}}:=\partial _{h_1,\ldots,\widehat {h_i},\ldots,h_{2s}}\phi (y_{\mathbf {h}}+\epsilon h_i)$,
$v_{i,\epsilon,\mathbf {h}}:=\partial _{h_1,\ldots,\widehat {h_i},\ldots,h_{2s}}\phi (y_{\mathbf {h}}+\epsilon h_i)$,
so that ![]() $\mu _{A_{\mathbf {h}}}(X_{\mathbf {h}})\gg _s\delta ^{O_s(1)}$, and
$\mu _{A_{\mathbf {h}}}(X_{\mathbf {h}})\gg _s\delta ^{O_s(1)}$, and
Note that ![]() $(x,x+k,x+k',x+k+k')\in X'_{\mathbf {h}}$ if and only if
$(x,x+k,x+k',x+k+k')\in X'_{\mathbf {h}}$ if and only if
for all ![]() $i=1,\ldots,2s$,
$i=1,\ldots,2s$, ![]() $\epsilon =0,1$, and
$\epsilon =0,1$, and ![]() $\omega '\in \{0,1\}^2$. Thus, whenever
$\omega '\in \{0,1\}^2$. Thus, whenever ![]() $(x,x+k,x+k',x+k+k')\in X'_{\mathbf {h}}$, we have
$(x,x+k,x+k',x+k+k')\in X'_{\mathbf {h}}$, we have
 \begin{align*} \partial_{h_1,\ldots,h_{2s},k}\phi(x)=\partial_{h_1,\ldots,h_{2s},k'} \phi(x)=\partial_{h_1,\ldots,h_{2s},k}\phi(x+k')&=\partial_{h_1,\ldots,h_{2s},k'}\phi(x+k) \\ &=v_{1,0,\mathbf{h}}-v_{1,1,\mathbf{h}}-(v_{1,0,\mathbf{h}}-v_{1,1,\mathbf{h}}) \\ &=0 \end{align*}
\begin{align*} \partial_{h_1,\ldots,h_{2s},k}\phi(x)=\partial_{h_1,\ldots,h_{2s},k'} \phi(x)=\partial_{h_1,\ldots,h_{2s},k}\phi(x+k')&=\partial_{h_1,\ldots,h_{2s},k'}\phi(x+k) \\ &=v_{1,0,\mathbf{h}}-v_{1,1,\mathbf{h}}-(v_{1,0,\mathbf{h}}-v_{1,1,\mathbf{h}}) \\ &=0 \end{align*}
and
for all ![]() $i=1,\ldots,2s$ and
$i=1,\ldots,2s$ and ![]() $\epsilon =0,1$. That is, the derivative of
$\epsilon =0,1$. That is, the derivative of ![]() $\phi$ vanishes on all
$\phi$ vanishes on all ![]() $(2s+1)$-dimensional faces of the
$(2s+1)$-dimensional faces of the ![]() $(2s+2)$-dimensional parallelopiped
$(2s+2)$-dimensional parallelopiped ![]() $(x+\omega \cdot (h_1,\ldots,h_{2s},k,k'))_{\omega \in \{0,1\}^{2s+2}}$.
$(x+\omega \cdot (h_1,\ldots,h_{2s},k,k'))_{\omega \in \{0,1\}^{2s+2}}$.
As in the ![]() $s=0$ case,
$s=0$ case,
 \[ \delta^{O_s(1)}\mu_{\mathbb{F}_p^n}(A_{\mathbf{h}})\ll_s\|X_{\mathbf{h}}\|_{U^1(\mathbb{F}_p^n)}\leq \|X_{\mathbf{h}}\|_{U^2(\mathbb{F}_p^n)}=\bigg(\frac{\# X'_{\mathbf{h}}}{p^{3n}}\bigg)^{1/4}, \]
\[ \delta^{O_s(1)}\mu_{\mathbb{F}_p^n}(A_{\mathbf{h}})\ll_s\|X_{\mathbf{h}}\|_{U^1(\mathbb{F}_p^n)}\leq \|X_{\mathbf{h}}\|_{U^2(\mathbb{F}_p^n)}=\bigg(\frac{\# X'_{\mathbf{h}}}{p^{3n}}\bigg)^{1/4}, \]
so that
for at least a ![]() $\Omega _s(\delta ^{O_s(1)})$-proportion of
$\Omega _s(\delta ^{O_s(1)})$-proportion of ![]() $2s$-tuples
$2s$-tuples ![]() $\mathbf {h}$. Each ordered quadruple
$\mathbf {h}$. Each ordered quadruple ![]() $(x,\mathbf {h},k,k')$ for which
$(x,\mathbf {h},k,k')$ for which ![]() $(x,x+k,x+k',x+k+k')\in X_{\mathbf {h}}'$ corresponds to a unique
$(x,x+k,x+k',x+k+k')\in X_{\mathbf {h}}'$ corresponds to a unique ![]() $(2s+2)$-dimensional parallelopiped
$(2s+2)$-dimensional parallelopiped
in ![]() $A^{2s+2}$. Thus,
$A^{2s+2}$. Thus,
 \begin{align*}
&\#\{P(x,\mathbf{h},k,k'):\mathbf{h}\in(\mathbb{F}_p^n)^{2s}\text{ and } (x,x+k,x+k',x+k+k')\in X_{\mathbf{h}}'\} \\
&\quad \gg_s\delta^{O_s(1)}(\alpha^{2^{2s+2}}+O([C_s(\alpha\delta)^{c_s}]^{\Omega(1)}))p^{(2s+3)n}.
\end{align*}
\begin{align*}
&\#\{P(x,\mathbf{h},k,k'):\mathbf{h}\in(\mathbb{F}_p^n)^{2s}\text{ and } (x,x+k,x+k',x+k+k')\in X_{\mathbf{h}}'\} \\
&\quad \gg_s\delta^{O_s(1)}(\alpha^{2^{2s+2}}+O([C_s(\alpha\delta)^{c_s}]^{\Omega(1)}))p^{(2s+3)n}.
\end{align*}
In comparison, the number of ![]() $(2s+2)$-dimensional parallelopipeds in
$(2s+2)$-dimensional parallelopipeds in ![]() $A$ is
$A$ is
by Corollary 3.3. The conclusion of the lemma now follows as long as ![]() $C_s$ is sufficiently small and
$C_s$ is sufficiently small and ![]() $c_s$ is sufficiently large.
$c_s$ is sufficiently large.
With a bit more work, it is possible to prove a version of Lemma 4.4 with ![]() $(2s+2)$-dimensional parallelopipeds replaced by
$(2s+2)$-dimensional parallelopipeds replaced by ![]() $(s+2)$-dimensional parallelopipeds (which is optimal), and thus a version of Lemma 4.1 with the
$(s+2)$-dimensional parallelopipeds (which is optimal), and thus a version of Lemma 4.1 with the ![]() $U^{2s+2}$-norm replaced by the
$U^{2s+2}$-norm replaced by the ![]() $U^{s+2}$-norm, but this would make a negligible difference in Theorem 1.2.
$U^{s+2}$-norm, but this would make a negligible difference in Theorem 1.2.
Now we can prove Lemma 4.1.
Proof of Lemma 4.1 We proceed by induction on ![]() $r$ and
$r$ and ![]() $s$, beginning with the
$s$, beginning with the ![]() $r=1$,
$r=1$, ![]() $s=0$ caseFootnote 1. Since
$s=0$ caseFootnote 1. Since ![]() $\operatorname {codim}\{y\in \mathbb {F}_p^n:\Phi (x,y)=1\}=d$ for all
$\operatorname {codim}\{y\in \mathbb {F}_p^n:\Phi (x,y)=1\}=d$ for all ![]() $x\in A$, certainly
$x\in A$, certainly
for all ![]() $\mathbf {x}\in (\mathbb {F}_p^n)^m$ for which
$\mathbf {x}\in (\mathbb {F}_p^n)^m$ for which ![]() $\psi _1(\mathbf {x})\in A$, and this case follows trivially without even needing the assumption that
$\psi _1(\mathbf {x})\in A$, and this case follows trivially without even needing the assumption that ![]() $\|\Phi -\alpha \rho \|_{U^2(\mathbb {F}_p^n\times \mathbb {F}_p^n)}$ is small.
$\|\Phi -\alpha \rho \|_{U^2(\mathbb {F}_p^n\times \mathbb {F}_p^n)}$ is small.
Now let ![]() $r\geq 2$ or
$r\geq 2$ or ![]() $s\geq 1$, and assume that the result holds for all pairs of integers
$s\geq 1$, and assume that the result holds for all pairs of integers ![]() $(r',s')$ satisfying:
$(r',s')$ satisfying:
(i)
 $0\leq r'< r$ and
$0\leq r'< r$ and  $1\leq s'\leq s$; or
$1\leq s'\leq s$; or(ii)
 $1\leq s'< s$;
$1\leq s'< s$;
and let ![]() $C'$ be at most the minimum of
$C'$ be at most the minimum of ![]() $C_{r',s'}$ and
$C_{r',s'}$ and ![]() $c'$ be at least the maximum of
$c'$ be at least the maximum of ![]() $c_{r',s'}$ over all such pairs with
$c_{r',s'}$ over all such pairs with ![]() $r'<\max (r,2^{s+1})$. As long as
$r'<\max (r,2^{s+1})$. As long as ![]() $\|\Phi -\alpha \rho \|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}< C'(\alpha \delta \rho ^{2r}/2)^{c'2^r}$, it follows from the induction hypothesis that for all but a
$\|\Phi -\alpha \rho \|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}< C'(\alpha \delta \rho ^{2r}/2)^{c'2^r}$, it follows from the induction hypothesis that for all but a ![]() $O(\delta )$-proportion of
$O(\delta )$-proportion of ![]() $\mathbf {x}\in (\mathbb {F}_p^n)^m$ for which
$\mathbf {x}\in (\mathbb {F}_p^n)^m$ for which ![]() $\psi _1(\mathbf {x}),\ldots,\psi _r(\mathbf {x})\in A$, we must have
$\psi _1(\mathbf {x}),\ldots,\psi _r(\mathbf {x})\in A$, we must have
 \[ \mathbb{E}_{y}\prod_{i=1}^r(\Phi-\rho)(\psi_i(\mathbf{x}),y+w_i)= \mathbb{E}_{y}\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)-\rho^r \]
\[ \mathbb{E}_{y}\prod_{i=1}^r(\Phi-\rho)(\psi_i(\mathbf{x}),y+w_i)= \mathbb{E}_{y}\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)-\rho^r \]
for all ![]() $w_1,\ldots,w_r\in \mathbb {F}_p^n$. If the codimension of some
$w_1,\ldots,w_r\in \mathbb {F}_p^n$. If the codimension of some ![]() $\{y\in \mathbb {F}_p^n:\prod _{i=1}^{r}\Phi (\psi _i(\mathbf {x}),y+w_i)=1\}$ is not
$\{y\in \mathbb {F}_p^n:\prod _{i=1}^{r}\Phi (\psi _i(\mathbf {x}),y+w_i)=1\}$ is not ![]() $rd$ for one of these typical
$rd$ for one of these typical ![]() $\mathbf {x}$, then it is either
$\mathbf {x}$, then it is either ![]() $n$ or at most
$n$ or at most ![]() $rd-1$, which means that
$rd-1$, which means that
 \begin{equation} \bigg|\mathbb{E}_{y}\prod_{i=1}^r(\Phi-\rho)(\psi_i(\mathbf{x}),y+w_i)\bigg|\geq\frac{\rho^r}{2} \end{equation}
\begin{equation} \bigg|\mathbb{E}_{y}\prod_{i=1}^r(\Phi-\rho)(\psi_i(\mathbf{x}),y+w_i)\bigg|\geq\frac{\rho^r}{2} \end{equation}
in either case, since ![]() $p\geq 2$. Squaring both sides of (22), multiplying by
$p\geq 2$. Squaring both sides of (22), multiplying by ![]() $\prod _{i=1}^rA(\psi _i(\mathbf {x}))$, averaging over all
$\prod _{i=1}^rA(\psi _i(\mathbf {x}))$, averaging over all ![]() $\mathbf {x}\in (\mathbb {F}_p^n)^m$, swapping the order of summation, and applying Lemma 4.2 (to deduce the uniformity of
$\mathbf {x}\in (\mathbb {F}_p^n)^m$, swapping the order of summation, and applying Lemma 4.2 (to deduce the uniformity of ![]() $A$) and Theorem 3.2 yields
$A$) and Theorem 3.2 yields
By Hölder's inequality, we then have
It follows from this, the induction hypothesis, our assumption that ![]() $\|\Phi -\alpha \rho \|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}< C'(\alpha \delta \rho ^{2r}/2)^{c'2^r}$, and Lemma 4.2 that
$\|\Phi -\alpha \rho \|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}< C'(\alpha \delta \rho ^{2r}/2)^{c'2^r}$, and Lemma 4.2 that
since the Cauchy–Schwarz complexity of any proper subset of
is at most ![]() $s-1$.
$s-1$.
Thus, by taking ![]() $C'$ sufficiently small and
$C'$ sufficiently small and ![]() $c'$ sufficiently large, we get that
$c'$ sufficiently large, we get that
for at least an ![]() $\Omega _s((\delta \rho )^{O_s(1)})$-proportion of
$\Omega _s((\delta \rho )^{O_s(1)})$-proportion of ![]() $(s+2)$-tuples
$(s+2)$-tuples ![]() $(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which
$(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which ![]() $(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$. The condition (23) implies that, for each such
$(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$. The condition (23) implies that, for each such ![]() $(x,h_1,\ldots,h_{s+1})$, there exist vectors
$(x,h_1,\ldots,h_{s+1})$, there exist vectors ![]() $v_{x,\mathbf {h},\omega }\in V^{\perp }_{x+\omega \cdot \mathbf {h}}$,
$v_{x,\mathbf {h},\omega }\in V^{\perp }_{x+\omega \cdot \mathbf {h}}$, ![]() $\omega \in \{0,1\}^{s+1}$, not all of which are zero, such that
$\omega \in \{0,1\}^{s+1}$, not all of which are zero, such that
Fix a basis ![]() $\{\gamma _{z,1},\ldots,\gamma _{z,d}\}$ of
$\{\gamma _{z,1},\ldots,\gamma _{z,d}\}$ of ![]() $V_z^\perp$ for each
$V_z^\perp$ for each ![]() $z\in \mathbb {F}_p^n$. We can write every vector
$z\in \mathbb {F}_p^n$. We can write every vector ![]() $v_{x,\mathbf {h},\omega }$ in terms of this basis, giving us that
$v_{x,\mathbf {h},\omega }$ in terms of this basis, giving us that
 \begin{align*} \sum_{\omega\in\{0,1\}^{s+1}}\sum_{j=1}^db_{x,\mathbf{h},\omega,j}\gamma_{x+\omega\cdot\mathbf{h},j}=0 \end{align*}
\begin{align*} \sum_{\omega\in\{0,1\}^{s+1}}\sum_{j=1}^db_{x,\mathbf{h},\omega,j}\gamma_{x+\omega\cdot\mathbf{h},j}=0 \end{align*}
for some ![]() $2^{s+1}d$-tuple of constants
$2^{s+1}d$-tuple of constants ![]() $(b_{x,\mathbf {h},\omega,j})_{\omega \in \{0,1\}^{s+1},\ 1\leq j\leq d}$, not all of which are zero.
$(b_{x,\mathbf {h},\omega,j})_{\omega \in \{0,1\}^{s+1},\ 1\leq j\leq d}$, not all of which are zero.
We apply the pigeonhole principle to deduce that there is some ![]() $2^{s+1}d$-tuple of constants
$2^{s+1}d$-tuple of constants ![]() $(b_{\omega,j})_{\omega \in \{0,1\}^{s+1},\ 1\leq j\leq d}$, not all of which are zero, such that
$(b_{\omega,j})_{\omega \in \{0,1\}^{s+1},\ 1\leq j\leq d}$, not all of which are zero, such that
 \[ \sum_{\omega\in\{0,1\}^{s+1}}\sum_{j=1}^db_{\omega,j}\gamma_{x+\omega\cdot\mathbf{h},j}=0 \]
\[ \sum_{\omega\in\{0,1\}^{s+1}}\sum_{j=1}^db_{\omega,j}\gamma_{x+\omega\cdot\mathbf{h},j}=0 \]
for at least a ![]() $\Omega _s((\delta \rho )^{O_s(1)})$-proportion of
$\Omega _s((\delta \rho )^{O_s(1)})$-proportion of ![]() $(s+2)$-tuples
$(s+2)$-tuples ![]() $(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which
$(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which ![]() $(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$. Defining
$(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$. Defining
 \[ \phi_{\omega}(z):=\sum_{j=1}^db_{\omega,j}\gamma_{z,j} \]
\[ \phi_{\omega}(z):=\sum_{j=1}^db_{\omega,j}\gamma_{z,j} \]
for each ![]() $\omega \in \{0,1\}^{s+1}$, the above says that, for at least a
$\omega \in \{0,1\}^{s+1}$, the above says that, for at least a ![]() $\Omega _s((\delta \rho )^{O_s(1)})$-proportion of
$\Omega _s((\delta \rho )^{O_s(1)})$-proportion of ![]() $(s+2)$-tuples
$(s+2)$-tuples ![]() $(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which
$(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which ![]() $(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$, we must have
$(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$, we must have
where at least one of the functions ![]() $\phi _{\omega }:\mathbb {F}_p^n\to \mathbb {F}_p^n$ does not have the zero vector in its image (because
$\phi _{\omega }:\mathbb {F}_p^n\to \mathbb {F}_p^n$ does not have the zero vector in its image (because ![]() $\phi _\omega (z)$ is always a nontrivial linear combination of linearly independent vectors). Let
$\phi _\omega (z)$ is always a nontrivial linear combination of linearly independent vectors). Let ![]() $\phi$ be any such
$\phi$ be any such ![]() $\phi _\omega$. It then follows by applying Corollary 3.3 to the inside average of
$\phi _\omega$. It then follows by applying Corollary 3.3 to the inside average of
 \[ \mathbb{E}_{y}\mathbb{E}_{x,h_1,\ldots,h_{s+1}}e_p \bigg(y\cdot\sum_{\omega\in\{0,1\}^{s+1}} \phi_\omega(x+\omega\cdot \mathbf{h})\bigg)A(\phi_\omega(x+\omega\cdot \mathbf{h})) \]
\[ \mathbb{E}_{y}\mathbb{E}_{x,h_1,\ldots,h_{s+1}}e_p \bigg(y\cdot\sum_{\omega\in\{0,1\}^{s+1}} \phi_\omega(x+\omega\cdot \mathbf{h})\bigg)A(\phi_\omega(x+\omega\cdot \mathbf{h})) \]
that ![]() $\partial _{h_1,\ldots,h_{s+1}}\phi (x)=0$ for at least a
$\partial _{h_1,\ldots,h_{s+1}}\phi (x)=0$ for at least a ![]() $\Omega _s((\delta \rho )^{O_s(1)})$-proportion of
$\Omega _s((\delta \rho )^{O_s(1)})$-proportion of ![]() $(s+2)$-tuples
$(s+2)$-tuples ![]() $(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which
$(x,h_1,\ldots,h_{s+1})\in (\mathbb {F}_p^n)^{s+2}$ for which ![]() $(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$, again provided that
$(x+\omega \cdot (h_1,\ldots,h_{s+1}))_{\omega \in \{0,1\}^{s+1}}\in A^{2^{s+1}}$, again provided that ![]() $C'$ is sufficiently small and
$C'$ is sufficiently small and ![]() $c'$ is sufficiently large. That is,
$c'$ is sufficiently large. That is, ![]() $\phi$ is a
$\phi$ is a ![]() $\Omega _s((\delta \rho )^{O_s(1)})$-approximate polynomial of degree at most
$\Omega _s((\delta \rho )^{O_s(1)})$-approximate polynomial of degree at most ![]() $s$ on
$s$ on ![]() $A$.
$A$.
If ![]() $C'$ is small enough and
$C'$ is small enough and ![]() $c'$ is large enough, Lemmas 4.2 and 4.4, then imply that for at least a
$c'$ is large enough, Lemmas 4.2 and 4.4, then imply that for at least a ![]() $\Omega _{s}((\alpha \delta \rho )^{O_s(1)})$-proportion of
$\Omega _{s}((\alpha \delta \rho )^{O_s(1)})$-proportion of ![]() $(2s+2)$-dimensional parallelopipeds
$(2s+2)$-dimensional parallelopipeds ![]() $(x+\omega \cdot (h_1,\ldots,h_{2s+2}))_{\omega \in \{0,1\}^{2s+2}}$ in
$(x+\omega \cdot (h_1,\ldots,h_{2s+2}))_{\omega \in \{0,1\}^{2s+2}}$ in ![]() $A^{2^{2s+2}}$, the derivative of
$A^{2^{2s+2}}$, the derivative of ![]() $\phi$ on each
$\phi$ on each ![]() $(2s+1)$-dimensional face vanishes, i.e.
$(2s+1)$-dimensional face vanishes, i.e.
 \[ \sum_{\substack{\omega\in\{0,1\}^{2s+2} \\ \omega_i=\epsilon}}(-1)^{|\omega|}\phi(x+\omega\cdot(h_1,\ldots,h_{2s+2}))=0 \]
\[ \sum_{\substack{\omega\in\{0,1\}^{2s+2} \\ \omega_i=\epsilon}}(-1)^{|\omega|}\phi(x+\omega\cdot(h_1,\ldots,h_{2s+2}))=0 \]
for all ![]() $i=1,\ldots,2s+2$ and
$i=1,\ldots,2s+2$ and ![]() $\epsilon =0,1$. Call the set of
$\epsilon =0,1$. Call the set of ![]() $(2s+3)$-tuples
$(2s+3)$-tuples ![]() $(x,h_1,\ldots,h_{2s+2})$ corresponding to such
$(x,h_1,\ldots,h_{2s+2})$ corresponding to such ![]() $(2s+2)$-dimensional parallelopipeds
$(2s+2)$-dimensional parallelopipeds ![]() $X$. Consider
$X$. Consider ![]() $\|\Phi -\rho A\|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}^{2^{2s+2}}$, which, plugging in the expression
$\|\Phi -\rho A\|_{U^{2s+2}(\mathbb {F}_p^n\times \mathbb {F}_p^n)}^{2^{2s+2}}$, which, plugging in the expression
for ![]() $\Phi -\rho A$, equals
$\Phi -\rho A$, equals
 \[ \rho^{2^{2s+2}}\mathbb{E}_{x,h_1,\ldots,h_{2s+2}}\Delta_{h_1,\ldots,h_{2s+2}}A(x) \sum_{\substack{0\neq v_\omega\in V_{x+\omega\cdot\mathbf{h}}^\perp \\ \omega\in\{0,1\}^{2s+2}}}\prod_{\substack{1\leq i\leq 2s+2 \\ \epsilon=0,1}}1_{\mathbf{0}}\bigg(\sum_{\substack{\omega\in\{0,1\}^{2s+2} \\ \omega_i=\epsilon}}(-1)^{|\omega|}v_\omega\bigg). \]
\[ \rho^{2^{2s+2}}\mathbb{E}_{x,h_1,\ldots,h_{2s+2}}\Delta_{h_1,\ldots,h_{2s+2}}A(x) \sum_{\substack{0\neq v_\omega\in V_{x+\omega\cdot\mathbf{h}}^\perp \\ \omega\in\{0,1\}^{2s+2}}}\prod_{\substack{1\leq i\leq 2s+2 \\ \epsilon=0,1}}1_{\mathbf{0}}\bigg(\sum_{\substack{\omega\in\{0,1\}^{2s+2} \\ \omega_i=\epsilon}}(-1)^{|\omega|}v_\omega\bigg). \]
The above has size ![]() $\gg _s(p-1)(\alpha \rho )^{2^{2s+2}}(\alpha \delta \rho )^{O_s(1)}\gg _s(\alpha \delta \rho )^{O_s(1)}$, coming from the contribution of
$\gg _s(p-1)(\alpha \rho )^{2^{2s+2}}(\alpha \delta \rho )^{O_s(1)}\gg _s(\alpha \delta \rho )^{O_s(1)}$, coming from the contribution of ![]() $v_\omega =\lambda \phi (x+\omega \cdot (h_1,\ldots,h_{2s+2}))$ for each
$v_\omega =\lambda \phi (x+\omega \cdot (h_1,\ldots,h_{2s+2}))$ for each ![]() $\lambda \in \mathbb {F}_p^\times$ and
$\lambda \in \mathbb {F}_p^\times$ and ![]() $(x,h_1,\ldots,h_{2s+2})\in X$. On the other hand, we have
$(x,h_1,\ldots,h_{2s+2})\in X$. On the other hand, we have
 \begin{align*} \|\Phi-\rho A\|_{U^{2s+2}(\mathbb{F}_p^n\times\mathbb{F}_p^n)} &= \|\Phi-\rho\alpha+ \rho\alpha-\rho A\|_{U^{2s+2}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}\\ &\leq \|\Phi-\rho\alpha\|_{U^{2s+2}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}+\rho\|A-\alpha\|_{U^{2s+2}(\mathbb{F}_p^n)}, \end{align*}
\begin{align*} \|\Phi-\rho A\|_{U^{2s+2}(\mathbb{F}_p^n\times\mathbb{F}_p^n)} &= \|\Phi-\rho\alpha+ \rho\alpha-\rho A\|_{U^{2s+2}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}\\ &\leq \|\Phi-\rho\alpha\|_{U^{2s+2}(\mathbb{F}_p^n\times\mathbb{F}_p^n)}+\rho\|A-\alpha\|_{U^{2s+2}(\mathbb{F}_p^n)}, \end{align*}
so that
Taking ![]() $C_{s,r}$ sufficiently small and
$C_{s,r}$ sufficiently small and ![]() $c_{s,r}$ sufficiently large will thus yield a contradiction if
$c_{s,r}$ sufficiently large will thus yield a contradiction if
 \[ \operatorname{codim}\bigg\{y\in\mathbb{F}_p^n:\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)=1\bigg\}\neq rd \]
\[ \operatorname{codim}\bigg\{y\in\mathbb{F}_p^n:\prod_{i=1}^r\Phi(\psi_i(\mathbf{x}),y+w_i)=1\bigg\}\neq rd \]
for some ![]() $w_1,\ldots,w_r\in \mathbb {F}_p^n$ for a
$w_1,\ldots,w_r\in \mathbb {F}_p^n$ for a ![]() $\delta$-proportion of
$\delta$-proportion of ![]() $\mathbf {x}\in (\mathbb {F}_p^n)^m$ for which
$\mathbf {x}\in (\mathbb {F}_p^n)^m$ for which ![]() $\psi _1(\mathbf {x}),\ldots,\psi _r(\mathbf {x})\in A$.
$\psi _1(\mathbf {x}),\ldots,\psi _r(\mathbf {x})\in A$.
5. Control by directional uniformity norms
This section is devoted to proving Lemmas 2.3 and 2.4. Our arguments mostly consist of careful, repeated applications of the Cauchy–Schwarz inequality to ensure that there is no loss of density factors and using the results of §§ 3 and 4 to analyze the resulting averages. As a simple warm-up, we begin by showing that if ![]() $T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has the form (11) and
$T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has the form (11) and ![]() $B,C,$ and
$B,C,$ and ![]() $D$ are sufficiently pseudorandom, then
$D$ are sufficiently pseudorandom, then ![]() $T$ has density close to the product density
$T$ has density close to the product density ![]() $\alpha \beta \gamma \delta \rho$.
$\alpha \beta \gamma \delta \rho$.
Lemma 5.1 Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Let
$\rho :=p^{-d}$. Let ![]() $\varepsilon >0$ and assume that
$\varepsilon >0$ and assume that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,$ and
$\alpha,\beta,\gamma,$ and ![]() $\delta$, respectively, and satisfy
$\delta$, respectively, and satisfy
and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Then the set
$d$. Then the set ![]() $T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ defined by (11) has density
$T\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ defined by (11) has density
Proof. The density of ![]() $T$ in
$T$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ can be written as
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ can be written as
where ![]() $F(x,y):=B(y)C(x+y)D(2x+y)$. Set
$F(x,y):=B(y)C(x+y)D(2x+y)$. Set ![]() $L(x,y):=\{y,x+y,2x+y\}$. Lemma 3.6 says that
$L(x,y):=\{y,x+y,2x+y\}$. Lemma 3.6 says that
since
has Cauchy–Schwarz complexity at most ![]() $3$. Thus, Lemma 3.5 yields
$3$. Thus, Lemma 3.5 yields
for all but a ![]() $O(\sqrt {\varepsilon })$-proportion of
$O(\sqrt {\varepsilon })$-proportion of ![]() $x\in \mathbb {F}_p^n$, so that
$x\in \mathbb {F}_p^n$, so that
Now we can prove Lemma 2.3.
Proof of Lemma 2.3 The quantity of interest ![]() $\Lambda (T,T,T,S)$ is
$\Lambda (T,T,T,S)$ is
which, after a change of variables, can be written as
where ![]() $\mu (x,y)$ equals
$\mu (x,y)$ equals
We will show that ![]() $\mu (x,y)$ is very close to the constant value
$\mu (x,y)$ is very close to the constant value ![]() $\alpha \beta ^2\gamma ^2\delta ^2\rho ^2$ for almost every pair
$\alpha \beta ^2\gamma ^2\delta ^2\rho ^2$ for almost every pair ![]() $(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n$, from which it will then follow that
$(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n$, from which it will then follow that ![]() $\Lambda (T,T,T,S)$ is close to
$\Lambda (T,T,T,S)$ is close to ![]() $\sigma \alpha ^2\beta ^3\gamma ^3\delta ^3\rho ^3$.
$\sigma \alpha ^2\beta ^3\gamma ^3\delta ^3\rho ^3$.
The first moment ![]() $\mathbb {E}_{x,y}\mu (x,y)$ equals
$\mathbb {E}_{x,y}\mu (x,y)$ equals
Applying Lemma 3.6 yields
where
It therefore follows from Lemma 3.5 that
for all but a ![]() $O(\sqrt {\varepsilon })$-proportion of
$O(\sqrt {\varepsilon })$-proportion of ![]() $(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n$. Thus,
$(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n$. Thus,
By arguing as in the proof of Lemma 5.1, we have
and, thus, conclude that
The second moment ![]() $\mathbb {E}_{x,y}\mu (x,y)^2$ equals
$\mathbb {E}_{x,y}\mu (x,y)^2$ equals
Applying Lemma 3.6 again yields
where
and applying Lemma 4.1 yields
for all ![]() $y\in \mathbb {F}_p^n$. Thus, by Lemma 3.5,
$y\in \mathbb {F}_p^n$. Thus, by Lemma 3.5,
for all but a ![]() $O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$-proportion of
$O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$-proportion of ![]() $(x,x+h,y)\in A\times A\times \mathbb {F}_p^n$, so that
$(x,x+h,y)\in A\times A\times \mathbb {F}_p^n$, so that
By Lemmas 3.6 and 4.1 again, we have
and
where
so that
by Lemma 3.5. Using Corollary 3.3 to estimate ![]() $\mathbb {E}_{x,h}\Delta _{-h}A(x)$, we thus conclude that
$\mathbb {E}_{x,h}\Delta _{-h}A(x)$, we thus conclude that
Our estimates for the first and second moments of ![]() $\mu$ imply that
$\mu$ imply that ![]() $\mu$ has variance
$\mu$ has variance ![]() $\mathbb {E}_{x,y}|\mu (x,y)-\alpha \beta ^2\gamma ^2\delta ^2\rho |^2\ll \varepsilon ^{\Omega (1)}/\rho ^{O(1)}$. It follows that
$\mathbb {E}_{x,y}|\mu (x,y)-\alpha \beta ^2\gamma ^2\delta ^2\rho |^2\ll \varepsilon ^{\Omega (1)}/\rho ^{O(1)}$. It follows that
 \begin{align*} \mathbb{E}_{x,y}S(x,y)\mu(x,y) &= \sigma\alpha^2\beta^3\gamma^3\delta^3\rho^3+O (\mathbb{E}_{x,y}|\mu(x,y)-\alpha\beta^2\gamma^2\delta^2\rho^2|) \\ &= \sigma\alpha^2\beta^3\gamma^3\delta^3\rho^3+O ([\mathbb{E}_{x,y}|\mu(x,y)-\alpha\beta^2\gamma^2\delta^2\rho^2|^2]^{1/2}) \\ &= \sigma\alpha^2\beta^3\gamma^3\delta^3\rho^3+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg). \end{align*}
\begin{align*} \mathbb{E}_{x,y}S(x,y)\mu(x,y) &= \sigma\alpha^2\beta^3\gamma^3\delta^3\rho^3+O (\mathbb{E}_{x,y}|\mu(x,y)-\alpha\beta^2\gamma^2\delta^2\rho^2|) \\ &= \sigma\alpha^2\beta^3\gamma^3\delta^3\rho^3+O ([\mathbb{E}_{x,y}|\mu(x,y)-\alpha\beta^2\gamma^2\delta^2\rho^2|^2]^{1/2}) \\ &= \sigma\alpha^2\beta^3\gamma^3\delta^3\rho^3+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg). \end{align*}
When ![]() $c_1$ is sufficiently small and
$c_1$ is sufficiently small and ![]() $c_2$ is sufficiently large, this gives the desired lower bound for
$c_2$ is sufficiently large, this gives the desired lower bound for ![]() $\Lambda (T,T,T,S)$.
$\Lambda (T,T,T,S)$.
To finish this section, we prove Lemma 2.4.
Proof of Lemma 2.4 We prove (16), (17), and then (18), proceeding in decreasing order of the number of applications of Cauchy–Schwarz required. For (16), we make the change of variables ![]() $z\mapsto z-x-y$ to write
$z\mapsto z-x-y$ to write ![]() $\Lambda (f_0,f_1,f_2,f_3)$ as
$\Lambda (f_0,f_1,f_2,f_3)$ as
which, by applying the Cauchy–Schwarz inequality in the ![]() $x$ and
$x$ and ![]() $z$ variables, has modulus squared bounded by
$z$ variables, has modulus squared bounded by
The first factor equals ![]() $\alpha \beta \gamma \delta \rho +O(\varepsilon ^{1/8})$ by Lemma 5.1. Expanding the square and making a change of variables, the second factor equals
$\alpha \beta \gamma \delta \rho +O(\varepsilon ^{1/8})$ by Lemma 5.1. Expanding the square and making a change of variables, the second factor equals
By another application of the Cauchy–Schwarz inequality in the ![]() $y,z,$ and
$y,z,$ and ![]() $h_1$ variables, the modulus squared of this is at most
$h_1$ variables, the modulus squared of this is at most
times
 \begin{align*}
\mathbb{E}_{y,z,h_1} ( & C(z)\Delta_{(-h_1,h_1)}\Phi(z-y,y)|\mathbb{E}_{x}B(z-x)D(x+z)\\ & \Delta_{(0,h_1)}f_0(x,y)\Delta_{(0,-h_1)}f_2(x,2z-2x-y)|^2).
\end{align*}
\begin{align*}
\mathbb{E}_{y,z,h_1} ( & C(z)\Delta_{(-h_1,h_1)}\Phi(z-y,y)|\mathbb{E}_{x}B(z-x)D(x+z)\\ & \Delta_{(0,h_1)}f_0(x,y)\Delta_{(0,-h_1)}f_2(x,2z-2x-y)|^2).
\end{align*}
The first factor (24) can be estimated in the same manner as the averages appearing in the proof of Lemma 2.3, and equals ![]() $\alpha ^2\beta ^2\gamma \delta ^2\rho ^2+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Expanding the square and making a change of variables, we get that the second factor equals
$\alpha ^2\beta ^2\gamma \delta ^2\rho ^2+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Expanding the square and making a change of variables, we get that the second factor equals
A final application of the Cauchy–Schwarz inequality in the ![]() $x,y,h_1,$ and
$x,y,h_1,$ and ![]() $h_2$ variables bounds the modulus squared of this by
$h_2$ variables bounds the modulus squared of this by
times
 \begin{align*}
\mathbb{E}_{x,y,h_1,h_2}&\Delta_{-h_1,-2h_2}B(y)\Delta_{-h_1,-h_2}C(x+y)\Delta_{-h_1}D(2x+y)
\Delta_{(h_2,-2h_2)}\Phi(x,y)\\ &
\cdot|\mathbb{E}_{z}\Delta_{-h_2}B(y-z)C(x+y-z)\Delta_{h_2}D(2x+y-z)\Delta_{(-h_1,h_1)}\Phi(x+z,y-2z)\\
&\Delta_{(0,h_1),(h_2,0)}f_0(x,y-2z)|^2
\end{align*}
\begin{align*}
\mathbb{E}_{x,y,h_1,h_2}&\Delta_{-h_1,-2h_2}B(y)\Delta_{-h_1,-h_2}C(x+y)\Delta_{-h_1}D(2x+y)
\Delta_{(h_2,-2h_2)}\Phi(x,y)\\ &
\cdot|\mathbb{E}_{z}\Delta_{-h_2}B(y-z)C(x+y-z)\Delta_{h_2}D(2x+y-z)\Delta_{(-h_1,h_1)}\Phi(x+z,y-2z)\\
&\Delta_{(0,h_1),(h_2,0)}f_0(x,y-2z)|^2
\end{align*}
By Lemmas 3.6 and 4.1, we have
 \begin{gather*} \mathbb{P}((x,y,h_2)\in\mathbb{F}_p^n\times\mathbb{F}_p^n\times\mathbb{F}_p^n:\|F(x,y,h_2,\cdot)-\beta^2\gamma^2 \delta\|_{U^2(\mathbb{F}_p^n)}>\varepsilon^{1/8})\ll\sqrt{\varepsilon},\\ \mathbb{P}((x,h_2)\in\mathbb{F}_p^n\times\mathbb{F}_p^n:\|G(x,h_2,\cdot)-\beta^2\gamma^2\delta\|_{U^2(\mathbb{F}_p^n)}>\varepsilon^{1/8}) \ll\sqrt{\varepsilon},\\ \mathbb{P}((x,x+h_2)\in A\times A:\operatorname{codim} \{h_1\in\mathbb{F}_p^n:\Delta_{(h_2,-2h_2)}\Phi(x,y-h_1)=1\}\neq 2d) \ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}} \end{gather*}
\begin{gather*} \mathbb{P}((x,y,h_2)\in\mathbb{F}_p^n\times\mathbb{F}_p^n\times\mathbb{F}_p^n:\|F(x,y,h_2,\cdot)-\beta^2\gamma^2 \delta\|_{U^2(\mathbb{F}_p^n)}>\varepsilon^{1/8})\ll\sqrt{\varepsilon},\\ \mathbb{P}((x,h_2)\in\mathbb{F}_p^n\times\mathbb{F}_p^n:\|G(x,h_2,\cdot)-\beta^2\gamma^2\delta\|_{U^2(\mathbb{F}_p^n)}>\varepsilon^{1/8}) \ll\sqrt{\varepsilon},\\ \mathbb{P}((x,x+h_2)\in A\times A:\operatorname{codim} \{h_1\in\mathbb{F}_p^n:\Delta_{(h_2,-2h_2)}\Phi(x,y-h_1)=1\}\neq 2d) \ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}} \end{gather*}
for all ![]() $y\in \mathbb {F}_p^n$, and
$y\in \mathbb {F}_p^n$, and
where
and
It then follows from Lemma 3.5 that (25) equals
which equals
It remains to relate
 \begin{align*}
\mathbb{E}_{x,y,h_1,h_2}&\Delta_{-h_1,-2h_2}B(y)\Delta_{-h_1,-h_2}C(x+y)
\Delta_{-h_1}D(2x+y)\Delta_{(h_2,-2h_2)}\Phi(x,y)\\ &
\cdot|\mathbb{E}_{z}\Delta_{-h_2}B(y-z)C(x+y-z)\Delta_{h_2}D(2x+y-z)\Delta_{(-h_1,h_1)}\Phi(x+z,y-2z)\\
&\Delta_{(0,h_1),(h_2,0)}f_0(x,y-2z)|^2
\end{align*}
\begin{align*}
\mathbb{E}_{x,y,h_1,h_2}&\Delta_{-h_1,-2h_2}B(y)\Delta_{-h_1,-h_2}C(x+y)
\Delta_{-h_1}D(2x+y)\Delta_{(h_2,-2h_2)}\Phi(x,y)\\ &
\cdot|\mathbb{E}_{z}\Delta_{-h_2}B(y-z)C(x+y-z)\Delta_{h_2}D(2x+y-z)\Delta_{(-h_1,h_1)}\Phi(x+z,y-2z)\\
&\Delta_{(0,h_1),(h_2,0)}f_0(x,y-2z)|^2
\end{align*}
to ![]() $\|f_0\|_{\star _1}$. Expanding the square and making a change of variables yields
$\|f_0\|_{\star _1}$. Expanding the square and making a change of variables yields
 \begin{align*} \mathbb{E}_{x,y,z,h_1,h_2,h_3}(&\Delta_{-h_1,-2h_2}B(y+2z)\Delta_{-h_2,-h_3}B(y+z) \\ &\Delta_{-h_1,-h_2}C(x+y+2z)\Delta_{-h_3}C(x+y+z) \\ &\Delta_{-h_1}D(2x+y+2z)\Delta_{h_2,-h_3}D(2x+y+z)\\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y) \\ &\Delta_{(0,h_1),(h_2,0),(0,-2h_3)}f_0(x,y)), \end{align*}
\begin{align*} \mathbb{E}_{x,y,z,h_1,h_2,h_3}(&\Delta_{-h_1,-2h_2}B(y+2z)\Delta_{-h_2,-h_3}B(y+z) \\ &\Delta_{-h_1,-h_2}C(x+y+2z)\Delta_{-h_3}C(x+y+z) \\ &\Delta_{-h_1}D(2x+y+2z)\Delta_{h_2,-h_3}D(2x+y+z)\\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y) \\ &\Delta_{(0,h_1),(h_2,0),(0,-2h_3)}f_0(x,y)), \end{align*}
which can be written as
where
 \begin{align*} \mu(x,y,h_1,h_2,h_3) := \mathbb{E}_{z}(&\Delta_{-h_1,-2h_2}B(y+2z)\Delta_{-h_2,-h_3}B(y+z) \\ &\Delta_{-h_1,-h_2}C(x+y+2z)\Delta_{-h_3}C(x+y+z) \\ &\Delta_{-h_1}D(2x+y+2z)\Delta_{h_2,-h_3}D(2x+y+z)\\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y)). \end{align*}
\begin{align*} \mu(x,y,h_1,h_2,h_3) := \mathbb{E}_{z}(&\Delta_{-h_1,-2h_2}B(y+2z)\Delta_{-h_2,-h_3}B(y+z) \\ &\Delta_{-h_1,-h_2}C(x+y+2z)\Delta_{-h_3}C(x+y+z) \\ &\Delta_{-h_1}D(2x+y+2z)\Delta_{h_2,-h_3}D(2x+y+z)\\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y)). \end{align*}
We will show that, for almost every ![]() $5$-tuple
$5$-tuple ![]() $(x,y,h_1,h_2,h_3)\in (\mathbb {F}_p^n)^5$ for which
$(x,y,h_1,h_2,h_3)\in (\mathbb {F}_p^n)^5$ for which ![]() $x,x+h_2\in A$,
$x,x+h_2\in A$, ![]() $\mu (x,y,h_1,h_2,h_3)$ is very close to the constant value
$\mu (x,y,h_1,h_2,h_3)$ is very close to the constant value ![]() $\alpha ^4\beta ^8\gamma ^6\delta ^6\rho ^{6}$. Indeed, the first moment
$\alpha ^4\beta ^8\gamma ^6\delta ^6\rho ^{6}$. Indeed, the first moment ![]() $\mathbb {E}_{\substack {x,y,h_1,h_2,h_3\\ x,x+h_2\in A}}\mu (x,y,h_1,h_2,h_3)$ is
$\mathbb {E}_{\substack {x,y,h_1,h_2,h_3\\ x,x+h_2\in A}}\mu (x,y,h_1,h_2,h_3)$ is
 \begin{align*} \frac{1}{\alpha^2+O(\varepsilon)}\mathbb{E}_{x,y,z,h_1,h_2,h_3}(&\Delta_{-h_1,-2h_2}B(y+2z)\Delta_{-h_2,-h_3}B(y+z) \\ &\Delta_{-h_1,-h_2}C(x+y+2z)\Delta_{-h_3}C(x+y+z) \\ &\Delta_{-h_1}D(2x+y+2z)\Delta_{h_2,-h_3}D(2x+y+z)\\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y)). \end{align*}
\begin{align*} \frac{1}{\alpha^2+O(\varepsilon)}\mathbb{E}_{x,y,z,h_1,h_2,h_3}(&\Delta_{-h_1,-2h_2}B(y+2z)\Delta_{-h_2,-h_3}B(y+z) \\ &\Delta_{-h_1,-h_2}C(x+y+2z)\Delta_{-h_3}C(x+y+z) \\ &\Delta_{-h_1}D(2x+y+2z)\Delta_{h_2,-h_3}D(2x+y+z)\\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y)). \end{align*}
Lemmas 3.6 and 4.1 tell us that
and
 \begin{align*} \mathbb{P}(&(x,x+h_2,x+z,x+z-h_1,x+z+h_3,x+z-h_1+h_3)\in A^6\\ &:\operatorname{codim}\{y\in\mathbb{F}_p^n:\Delta_{(h_2,-2h_2)}\Phi(x,y+2z) \Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y)=1\}\neq 6d)\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}, \end{align*}
\begin{align*} \mathbb{P}(&(x,x+h_2,x+z,x+z-h_1,x+z+h_3,x+z-h_1+h_3)\in A^6\\ &:\operatorname{codim}\{y\in\mathbb{F}_p^n:\Delta_{(h_2,-2h_2)}\Phi(x,y+2z) \Delta_{(-h_1,h_1),(h_3,-2h_3)}\Phi(x+z,y)=1\}\neq 6d)\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}, \end{align*}
where
so it follows from Lemma 3.5 that the first moment equals
which equals
by Corollary 3.3. The second moment ![]() $\mathbb {E}_{\substack {x,y,h_1,h_2,h_3 \\ x,x+h_2\in A}}\mu (x,y,h_1,h_2,h_3)^2$ is
$\mathbb {E}_{\substack {x,y,h_1,h_2,h_3 \\ x,x+h_2\in A}}\mu (x,y,h_1,h_2,h_3)^2$ is
 \begin{align*} \frac{1}{\alpha^2+O(\varepsilon)}\mathbb{E}_{x,y,z,h_1,h_2,h_3,k} (&\Delta_{-h_1,-2h_2,2k}B(y+2z)\Delta_{-h_2,-h_3,k}B(y+z)\\ &\Delta_{-h_1,-h_2,2k}C(x+y+2z)\Delta_{-h_3,k}C(x+y+z)\\ &\Delta_{-h_1,2k}D(2x+y+2z)\Delta_{h_2,-h_3,k}D(2x+y+z) \\ &\Delta_{(h_2,-2h_2),(0,2k)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3),(k,0)}\Phi(x+z,y)), \end{align*}
\begin{align*} \frac{1}{\alpha^2+O(\varepsilon)}\mathbb{E}_{x,y,z,h_1,h_2,h_3,k} (&\Delta_{-h_1,-2h_2,2k}B(y+2z)\Delta_{-h_2,-h_3,k}B(y+z)\\ &\Delta_{-h_1,-h_2,2k}C(x+y+2z)\Delta_{-h_3,k}C(x+y+z)\\ &\Delta_{-h_1,2k}D(2x+y+2z)\Delta_{h_2,-h_3,k}D(2x+y+z) \\ &\Delta_{(h_2,-2h_2),(0,2k)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3),(k,0)}\Phi(x+z,y)), \end{align*}
which, noting that
we can write as
 \begin{align*} \mathbb{E}_{x,y,z,h_1,h_2,h_3,k}(&\Delta_{-h_1,-2h_2,2k}B(y+2z)\Delta_{-h_2,-h_3,k}B(y+z)\\ &\Delta_{-h_1,-h_2,2k}C(x+y+2z)\Delta_{-h_3,k}C(x+y+z)\\ &\Delta_{-h_1,2k}D(2x+y+2z)\Delta_{h_2,-h_3,k}D(2x+y+z) \\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3),(k,0)}\Phi(x+z,y) \\ &\Delta_{(h_2,-2h_2)}\Phi(x,2k-u)), \end{align*}
\begin{align*} \mathbb{E}_{x,y,z,h_1,h_2,h_3,k}(&\Delta_{-h_1,-2h_2,2k}B(y+2z)\Delta_{-h_2,-h_3,k}B(y+z)\\ &\Delta_{-h_1,-h_2,2k}C(x+y+2z)\Delta_{-h_3,k}C(x+y+z)\\ &\Delta_{-h_1,2k}D(2x+y+2z)\Delta_{h_2,-h_3,k}D(2x+y+z) \\ &\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1),(h_3,-2h_3),(k,0)}\Phi(x+z,y) \\ &\Delta_{(h_2,-2h_2)}\Phi(x,2k-u)), \end{align*}
Lemmas 3.6 and 4.1, analogously to the case of the first moment, tell us that
and
 \begin{align*} \mathbb{P}\bigg(&x\in A\cap (A-h_2)\text{ and }x+z\in \bigcap_{\omega\in\{0,1\}^8}(A-\omega\cdot(-h_1,h_3,k))\\ &:\operatorname{codim}\{y\in\mathbb{F}_p^n:\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1), (h_3,-2h_3),(k,0)}\Phi(x+z,y)=1\}\neq 10d\bigg)\\ &\quad \ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}, \end{align*}
\begin{align*} \mathbb{P}\bigg(&x\in A\cap (A-h_2)\text{ and }x+z\in \bigcap_{\omega\in\{0,1\}^8}(A-\omega\cdot(-h_1,h_3,k))\\ &:\operatorname{codim}\{y\in\mathbb{F}_p^n:\Delta_{(h_2,-2h_2)}\Phi(x,y+2z)\Delta_{(-h_1,h_1), (h_3,-2h_3),(k,0)}\Phi(x+z,y)=1\}\neq 10d\bigg)\\ &\quad \ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}, \end{align*}
where
 \begin{align*} I(x,z,h_1,h_2,h_3,k,y) := (&\Delta_{-h_1,-2h_2,2k}B(y+2z)\Delta_{-h_2,-h_3,k}B(y+z)\\ &\Delta_{-h_1,-h_2,2k}C(x+y+2z)\Delta_{-h_3,k}C(x+y+z)\\ &\Delta_{-h_1,2k}D(2x+y+2z)\Delta_{h_2,-h_3,k}D(2x+y+z)), \end{align*}
\begin{align*} I(x,z,h_1,h_2,h_3,k,y) := (&\Delta_{-h_1,-2h_2,2k}B(y+2z)\Delta_{-h_2,-h_3,k}B(y+z)\\ &\Delta_{-h_1,-h_2,2k}C(x+y+2z)\Delta_{-h_3,k}C(x+y+z)\\ &\Delta_{-h_1,2k}D(2x+y+2z)\Delta_{h_2,-h_3,k}D(2x+y+z)), \end{align*}
so it follows from Lemma 3.5 that the second moment equals ![]() $(\alpha ^2+O(\varepsilon ))^{-1}$ times
$(\alpha ^2+O(\varepsilon ))^{-1}$ times
To estimate the main term of (26), we note that
and apply Lemmas 3.6 and 4.1 again to get that
and
where
Thus, by Lemma 3.5, we have that
equals
which equals
by Corollary 3.3. It therefore follows that the second moment is
Thus,
and we conclude that
Putting everything together gives
as desired.
For (17), we make a change of variables and apply the Cauchy–Schwarz inequality to bound ![]() $|\Lambda (T,f_1,f_2,f_3)|^2$ by
$|\Lambda (T,f_1,f_2,f_3)|^2$ by
 \begin{align*}
\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(T)\cdot\mathbb{E}_{x,y} & B(y)C(x+y) \Phi(x,y)\\ & \cdot |\mathbb{E}_zC(x+y-2z)D(2x+y-2z)f_1(x,y-z)f_3(x+z,y-2z)|^2.
\end{align*}
\begin{align*}
\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(T)\cdot\mathbb{E}_{x,y} & B(y)C(x+y) \Phi(x,y)\\ & \cdot |\mathbb{E}_zC(x+y-2z)D(2x+y-2z)f_1(x,y-z)f_3(x+z,y-2z)|^2.
\end{align*}
Expanding the square in the second quantity and making a change of variables yields
By applying the Cauchy–Schwarz inequality again in the ![]() $x,y,$ and
$x,y,$ and ![]() $h_1$ variables, the modulus squared of this is bounded above by
$h_1$ variables, the modulus squared of this is bounded above by
times
 \begin{align*} \mathbb{E}_{x,y,h_1}(&\Delta_{-2h_1}B(y)D(2x+y)\Delta_{(h_1,-2h_1)}\Phi(x,y)\\ &|\mathbb{E}_{z}[B(y+2z)C(x+y+z)\Delta_{-2h_1}C(x+y-z)\Delta_{-2h_1}D(2x+y-2z)\Phi(x-z,y+2z)\\ &\ \ \ \ \ \Delta_{(0,-h_1)}f_1(x-z,y+z)]|^2). \end{align*}
\begin{align*} \mathbb{E}_{x,y,h_1}(&\Delta_{-2h_1}B(y)D(2x+y)\Delta_{(h_1,-2h_1)}\Phi(x,y)\\ &|\mathbb{E}_{z}[B(y+2z)C(x+y+z)\Delta_{-2h_1}C(x+y-z)\Delta_{-2h_1}D(2x+y-2z)\Phi(x-z,y+2z)\\ &\ \ \ \ \ \Delta_{(0,-h_1)}f_1(x-z,y+z)]|^2). \end{align*}
Expanding the square and making a change of variables, the second factor equals
 \begin{align*} \mathbb{E}_{x,y,z,h_1,h_2}&\Delta_{2h_2}B(y+z)\Delta_{-2h_1}B(y-z) \Delta_{-2h_1,-h_2}C(x+y-z)\Delta_{h_2}C(x+y+z)\\ &\Delta_{-2h_1,-2h_2}D(2x+y-z)D(2x+y+z)\Delta_{(-h_2,h_2)} \Phi(x,y+z)\Delta_{(h_1,-2h_1)}\Phi(x+z,y-z) \\ &\Delta_{(0,-h_1),(-h_2,h_2)}f_1(x,y), \end{align*}
\begin{align*} \mathbb{E}_{x,y,z,h_1,h_2}&\Delta_{2h_2}B(y+z)\Delta_{-2h_1}B(y-z) \Delta_{-2h_1,-h_2}C(x+y-z)\Delta_{h_2}C(x+y+z)\\ &\Delta_{-2h_1,-2h_2}D(2x+y-z)D(2x+y+z)\Delta_{(-h_2,h_2)} \Phi(x,y+z)\Delta_{(h_1,-2h_1)}\Phi(x+z,y-z) \\ &\Delta_{(0,-h_1),(-h_2,h_2)}f_1(x,y), \end{align*}
which we can write as
where
 \begin{align*} \mu'(x,y,h_1,h_2) := \mathbb{E}_{z}&\Delta_{2h_2}B(y+z)\Delta_{-2h_1}B(y-z) \Delta_{-2h_1,-h_2}C(x+y-z)\Delta_{h_2}C(x+y+z)\\ &\Delta_{-2h_1,-2h_2}D(2x+y-z)D(2x+y+z)\Delta_{(-h_2,h_2)}\Phi(x,y+z)\\ &\Delta_{(h_1,-2h_1)}\Phi(x+z,y-z). \end{align*}
\begin{align*} \mu'(x,y,h_1,h_2) := \mathbb{E}_{z}&\Delta_{2h_2}B(y+z)\Delta_{-2h_1}B(y-z) \Delta_{-2h_1,-h_2}C(x+y-z)\Delta_{h_2}C(x+y+z)\\ &\Delta_{-2h_1,-2h_2}D(2x+y-z)D(2x+y+z)\Delta_{(-h_2,h_2)}\Phi(x,y+z)\\ &\Delta_{(h_1,-2h_1)}\Phi(x+z,y-z). \end{align*}
The quantity (27) and the weight ![]() $\mu '$ can be analyzed in the same manner as the corresponding quantity and weight in the proof of (16), so that
$\mu '$ can be analyzed in the same manner as the corresponding quantity and weight in the proof of (16), so that
Finally, for (18), we make a change of variables and apply the Cauchy–Schwarz inequality to bound ![]() $|\Lambda (T,T,f_2,f_3)|^2$ by
$|\Lambda (T,T,f_2,f_3)|^2$ by ![]() $\mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)$ times
$\mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)$ times
 \begin{align*} \mathbb{E}_{x,y}B(y)C(x+y)\Phi(x,y)|\mathbb{E}_z &B(y+z)C(x+y-z)D(2x+y-2z)D(2x+y-z)\\ &\Phi(x-z,y+z)f_2(x-z,y+2z)|^2. \end{align*}
\begin{align*} \mathbb{E}_{x,y}B(y)C(x+y)\Phi(x,y)|\mathbb{E}_z &B(y+z)C(x+y-z)D(2x+y-2z)D(2x+y-z)\\ &\Phi(x-z,y+z)f_2(x-z,y+2z)|^2. \end{align*}
Expanding the square in the second quantity and making a change of variables yields
which can be written as
where
 \begin{align*} \mu''(x,y,h_1):=\mathbb{E}_{z}&B(y)C(x+y-z)\Phi(x+z,y-2z)\Delta_{h_1}B(y-z)\Delta_{-h_1}C(x+y-2z)\\ &\Delta_{-2h_1}D(2x+y-2z)\Delta_{-h_1}D(2x+y-z)\Delta_{(-h_1,h_1)}\Phi(x,y-z). \end{align*}
\begin{align*} \mu''(x,y,h_1):=\mathbb{E}_{z}&B(y)C(x+y-z)\Phi(x+z,y-2z)\Delta_{h_1}B(y-z)\Delta_{-h_1}C(x+y-2z)\\ &\Delta_{-2h_1}D(2x+y-2z)\Delta_{-h_1}D(2x+y-z)\Delta_{(-h_1,h_1)}\Phi(x,y-z). \end{align*}
This weight can again be analyzed in the same manner as the weights appearing in the proof of (16), giving
and completing the proof of the lemma.
6. Obtaining a density increment
As was mentioned in § 2, one ingredient in the proof of Theorem 2.5 is an inverse theorem for the ![]() $U^2(\Phi (x,\cdot ))$-norm localized to pseudorandom sets. Applying the standard, nonlocalized inverse theorem for the
$U^2(\Phi (x,\cdot ))$-norm localized to pseudorandom sets. Applying the standard, nonlocalized inverse theorem for the ![]() $U^2(\Phi (x,\cdot ))$-norm would yield a density increment that gets weaker as
$U^2(\Phi (x,\cdot ))$-norm would yield a density increment that gets weaker as ![]() $T$ becomes sparser, which is inadequate to close the density-increment iteration. To get a strong enough localized version of this inverse theorem, we will need to use the transference principle. The particular instance of it required is an immediate consequence of the dense model lemma from [Reference ZhaoZha14], which appears as Lemma 3.3 in that paper.
$T$ becomes sparser, which is inadequate to close the density-increment iteration. To get a strong enough localized version of this inverse theorem, we will need to use the transference principle. The particular instance of it required is an immediate consequence of the dense model lemma from [Reference ZhaoZha14], which appears as Lemma 3.3 in that paper.
Lemma 6.1 (Dense model lemma for the  $U^s$-norm on subspaces)
$U^s$-norm on subspaces)
For every natural number ![]() $s$, there exists a constant
$s$, there exists a constant ![]() $c_s>0$ such that the following holds. Let
$c_s>0$ such that the following holds. Let ![]() $\varepsilon >0$,
$\varepsilon >0$, ![]() $V\leq \mathbb {F}_p^n$ be a subspace, and
$V\leq \mathbb {F}_p^n$ be a subspace, and ![]() $f,\nu :V\to [0,\infty )$ be functions satisfying:
$f,\nu :V\to [0,\infty )$ be functions satisfying:
(i)
 $0\leq f\leq \nu$;
$0\leq f\leq \nu$;(ii)
 $\mathbb {E}_{x\in V}f(x)\leq 1$; and
$\mathbb {E}_{x\in V}f(x)\leq 1$; and(iii)
 $\|\nu -1\|_{U^s(V)}\leq \exp (-\varepsilon ^{-c_s})$.
$\|\nu -1\|_{U^s(V)}\leq \exp (-\varepsilon ^{-c_s})$.
Then there exists a ![]() $\tilde {f}:V\to [0,1]$ such that
$\tilde {f}:V\to [0,1]$ such that ![]() $\mathbb {E}_{x\in V}f(x)=\mathbb {E}_{x\in V}\tilde {f}(x)$ and
$\mathbb {E}_{x\in V}f(x)=\mathbb {E}_{x\in V}\tilde {f}(x)$ and ![]() $\|f-\tilde {f}\|_{U^s(V)}\leq \varepsilon$.
$\|f-\tilde {f}\|_{U^s(V)}\leq \varepsilon$.
One can see that this lemma is a consequence of Zhao's lemma by using the Gowers–Cauchy–Schwarz inequality to translate between his ![]() $(s,\varepsilon )$-discrepancy pair condition and our
$(s,\varepsilon )$-discrepancy pair condition and our ![]() $U^s$-uniformity condition.
$U^s$-uniformity condition.
In the course of the proof of Theorem 2.5, we will encounter various averages of linear forms that turn out to be controlled by certain degree ![]() $1$ and
$1$ and ![]() $2$ directional uniformity norms. Because of this, we will also need to obtain a density increment when these norms of the balanced function
$2$ directional uniformity norms. Because of this, we will also need to obtain a density increment when these norms of the balanced function ![]() $g_S=S-\sigma$ are large. The first two subsections of this section are devoted to proving that this is possible.
$g_S=S-\sigma$ are large. The first two subsections of this section are devoted to proving that this is possible.
6.1 Results on degree  $1$ norms
$1$ norms
We first show that the relevant fibers of any set of the form (11) typically have close to their average density, provided that ![]() $A,B,C,D,$ and
$A,B,C,D,$ and ![]() $\Phi$ are sufficiently pseudorandom.
$\Phi$ are sufficiently pseudorandom.
Lemma 6.2 Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has density
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has density ![]() $\alpha \rho$ in
$\alpha \rho$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ and takes the form
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ and takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\varepsilon >0$ and assume that
$\varepsilon >0$ and assume that
Define ![]() $T$ by (11). Then
$T$ by (11). Then
 \begin{align*} \mathbb{P}(x\in
A:|\mu_{\mathbb{F}_p^n}(T(x,\cdot))-\beta\gamma\delta\rho|>\varepsilon')&\ll\frac{\varepsilon^{1/8}}{(\varepsilon')^2\alpha},\\
\mathbb{P}(y\in
B:|\mu_{\mathbb{F}_p^n}(T(\cdot,y))-\alpha\gamma\delta\rho|>\varepsilon')&\ll\frac{\varepsilon^{1/8}}{(\varepsilon')^2\beta},\\
\mathbb{P}(z\in
C:|\mu_{\mathbb{F}_p^n}(T(\cdot,z-\cdot))-\alpha\beta\delta\rho|>\varepsilon')&\ll\frac{\varepsilon^{1/8}}{(\varepsilon')^2\gamma},
\end{align*}
\begin{align*} \mathbb{P}(x\in
A:|\mu_{\mathbb{F}_p^n}(T(x,\cdot))-\beta\gamma\delta\rho|>\varepsilon')&\ll\frac{\varepsilon^{1/8}}{(\varepsilon')^2\alpha},\\
\mathbb{P}(y\in
B:|\mu_{\mathbb{F}_p^n}(T(\cdot,y))-\alpha\gamma\delta\rho|>\varepsilon')&\ll\frac{\varepsilon^{1/8}}{(\varepsilon')^2\beta},\\
\mathbb{P}(z\in
C:|\mu_{\mathbb{F}_p^n}(T(\cdot,z-\cdot))-\alpha\beta\delta\rho|>\varepsilon')&\ll\frac{\varepsilon^{1/8}}{(\varepsilon')^2\gamma},
\end{align*}
and
for any ![]() $\varepsilon '>0$.
$\varepsilon '>0$.
Proof. From Lemma 5.1, we have ![]() $\mathbb {E}_{x\in A}\mu _{\mathbb {F}_p^n}(T(x,\cdot ))=\beta \gamma \delta \rho +O(\varepsilon ^{1/8}/\alpha )$. For the second moment, we argue as in § 5 to estimate
$\mathbb {E}_{x\in A}\mu _{\mathbb {F}_p^n}(T(x,\cdot ))=\beta \gamma \delta \rho +O(\varepsilon ^{1/8}/\alpha )$. For the second moment, we argue as in § 5 to estimate
using Lemmas 3.5 and 3.6, giving ![]() $\mathbb {E}_{x\in A}\mu _{\mathbb {F}_p^n}(T(x,\cdot ))^2=\beta ^2\gamma ^2\delta ^2\rho ^2+O(\varepsilon ^{1/8}/\alpha )$. It now follows from Markov's inequality that
$\mathbb {E}_{x\in A}\mu _{\mathbb {F}_p^n}(T(x,\cdot ))^2=\beta ^2\gamma ^2\delta ^2\rho ^2+O(\varepsilon ^{1/8}/\alpha )$. It now follows from Markov's inequality that
for all ![]() $\varepsilon '>0$. The three other estimates are proved analogously.
$\varepsilon '>0$. The three other estimates are proved analogously.
Now we can obtain a density increment when the degree ![]() $1$ uniformity norms controlled by
$1$ uniformity norms controlled by ![]() $\|\cdot \|_{\star _1}$ and
$\|\cdot \|_{\star _1}$ and ![]() $\|\cdot \|_{\star _2}$ are large. The proof is essentially an averaging argument, like the proof of the analogous Lemma 3.1 in [Reference GreenGre05a]. The most substantial new feature, which will arise many times in this section, is that we must now verify that the set on which we claim to have found a density increment actually has close to the correct density in
$\|\cdot \|_{\star _2}$ are large. The proof is essentially an averaging argument, like the proof of the analogous Lemma 3.1 in [Reference GreenGre05a]. The most substantial new feature, which will arise many times in this section, is that we must now verify that the set on which we claim to have found a density increment actually has close to the correct density in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$. In the case of corners, any product set
$\mathbb {F}_p^n\times \mathbb {F}_p^n$. In the case of corners, any product set ![]() $A\times B$ trivially has density equal to the product of the densities of
$A\times B$ trivially has density equal to the product of the densities of ![]() $A$ and
$A$ and ![]() $B$. This is not, in general, the case for sets of the form (11) unless further assumptions are made about
$B$. This is not, in general, the case for sets of the form (11) unless further assumptions are made about ![]() $A,B,C,D,$ and
$A,B,C,D,$ and ![]() $\Phi$.
$\Phi$.
Lemma 6.3 There exist absolute constants ![]() $0< c_1<1< c_2$ such that the following holds. Let
$0< c_1<1< c_2$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\tau >0$ and
$\tau >0$ and ![]() $\varepsilon \leq c_1(\tau \alpha \beta \gamma \delta \rho )^{c_2}$, and assume that
$\varepsilon \leq c_1(\tau \alpha \beta \gamma \delta \rho )^{c_2}$, and assume that
Define ![]() $T$ by (11), and let
$T$ by (11), and let ![]() $S\subset T$ have density
$S\subset T$ have density ![]() $\sigma$ in
$\sigma$ in ![]() $T$. Suppose that
$T$. Suppose that
or
Then ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\tau ^{O(1)})$ on some subset
$\sigma +\Omega (\tau ^{O(1)})$ on some subset ![]() $T'$ of
$T'$ of ![]() $T$ of the form
$T$ of the form
where the densities of ![]() $A',B',C'\subset \mathbb {F}_p^n$ are
$A',B',C'\subset \mathbb {F}_p^n$ are ![]() $\Omega (\tau ^{O(1)}\alpha )$,
$\Omega (\tau ^{O(1)}\alpha )$, ![]() $\Omega (\tau ^{O(1)}\beta )$, and
$\Omega (\tau ^{O(1)}\beta )$, and ![]() $\Omega (\tau ^{O(1)}\gamma )$, respectively.
$\Omega (\tau ^{O(1)}\gamma )$, respectively.
Proof. The assumption (28) can be written as
Since ![]() $\mu _{\mathbb {F}_p^n}(T(x,\cdot ))>2\beta \gamma \delta \rho$ for at most a
$\mu _{\mathbb {F}_p^n}(T(x,\cdot ))>2\beta \gamma \delta \rho$ for at most a ![]() $O(\varepsilon ^{1/8}/\alpha ^3\beta ^2\gamma ^2\delta ^2\rho ^2)$-proportion of
$O(\varepsilon ^{1/8}/\alpha ^3\beta ^2\gamma ^2\delta ^2\rho ^2)$-proportion of ![]() $x\in A$ by Lemma 6.2, it follows that, as long as
$x\in A$ by Lemma 6.2, it follows that, as long as ![]() $c_2$ is sufficiently large, there exists a subset
$c_2$ is sufficiently large, there exists a subset ![]() $A_0\subset A$ of relative density at least
$A_0\subset A$ of relative density at least ![]() $\tau /4$ for which
$\tau /4$ for which
for all ![]() $x\in A_0$, provided that
$x\in A_0$, provided that ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough. Note that
$c_2$ is large enough. Note that ![]() $\mathbb {E}_{y}g_S(x,y)$ is a real number, and thus is either positive or negative. There must therefore exist a subset
$\mathbb {E}_{y}g_S(x,y)$ is a real number, and thus is either positive or negative. There must therefore exist a subset ![]() $A_1\subset A_0$ of density at least
$A_1\subset A_0$ of density at least ![]() $1/2$ in
$1/2$ in ![]() $A_0$ such that either
$A_0$ such that either
for every ![]() $x\in A_1$ or
$x\in A_1$ or
for every ![]() $x\in A_1$.
$x\in A_1$.
In the first case, setting ![]() $A'=A_1$ and
$A'=A_1$ and ![]() $\alpha '=\mu _{\mathbb {F}_p^n}(A')$, we have
$\alpha '=\mu _{\mathbb {F}_p^n}(A')$, we have
by Lemma 6.2 whenever ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough, so that
$c_2$ is large enough, so that
Since ![]() $\mathbb {E}_{x,y}A'(x)B(y)C(x+y)D(2x+y)\Phi (x,y)=\alpha '\beta \gamma \delta \rho +O(\varepsilon ^{1/16}/\alpha )$ by Lemma 6.2, the conclusion of the lemma follows when
$\mathbb {E}_{x,y}A'(x)B(y)C(x+y)D(2x+y)\Phi (x,y)=\alpha '\beta \gamma \delta \rho +O(\varepsilon ^{1/16}/\alpha )$ by Lemma 6.2, the conclusion of the lemma follows when ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough by taking
$c_2$ is large enough by taking ![]() $B'=B$.
$B'=B$.
In the second case, setting ![]() $A'=A\setminus A_1$ and
$A'=A\setminus A_1$ and ![]() $\alpha '=\mu _{\mathbb {F}_p^n}(A')$, we use the fact that
$\alpha '=\mu _{\mathbb {F}_p^n}(A')$, we use the fact that ![]() $\mathbb {E}_{x,y}g_S(x,y)=0$ to deduce that
$\mathbb {E}_{x,y}g_S(x,y)=0$ to deduce that
whenever ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough. Note that
$c_2$ is large enough. Note that ![]() $\mathbb {E}_{x,y}A'(x)B(y)C(x+y)D(2x+y)\Phi (x,y)=\alpha '\beta \gamma \delta \rho +O(\varepsilon ^{1/16}/\alpha )$ in this case as well by Lemma 6.2, so the conclusion of the lemma will follow as long as
$\mathbb {E}_{x,y}A'(x)B(y)C(x+y)D(2x+y)\Phi (x,y)=\alpha '\beta \gamma \delta \rho +O(\varepsilon ^{1/16}/\alpha )$ in this case as well by Lemma 6.2, so the conclusion of the lemma will follow as long as ![]() $\alpha '=\Omega (\tau ^{O(1)}\alpha )$. But this also follows from Lemma 6.2, for we have
$\alpha '=\Omega (\tau ^{O(1)}\alpha )$. But this also follows from Lemma 6.2, for we have
The proof of the lemma starting from the assumptions (29) and (30) is essentially identical, but using the second and third probability estimates from Lemma 6.2, respectively.
6.2 Results on degree  $2$ norms
$2$ norms
To obtain a density increment when the relevant degree ![]() $2$ directional uniformity norms of
$2$ directional uniformity norms of ![]() $g_S$ are large, we first need to show that certain degree
$g_S$ are large, we first need to show that certain degree ![]() $2$ ‘inner products’ are controlled by the degree
$2$ ‘inner products’ are controlled by the degree ![]() $1$ directional uniformity norms studied in the previous subsection.
$1$ directional uniformity norms studied in the previous subsection.
Lemma 6.4 Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\varepsilon >0$ and assume that
$\varepsilon >0$ and assume that
Define ![]() $T$ by (11), and let
$T$ by (11), and let ![]() $S\subset T$ and
$S\subset T$ and ![]() $\tau >0$.
$\tau >0$.
If
 \begin{equation} \bigg|\mathbb{E}_{x,y,h,k}\prod_{\omega\in\{0,1\}^2}g_\omega((x,y)+\omega\cdot((0,h),(0,k)))\bigg|\geq \tau\alpha\beta^4\gamma^4\delta^4\rho^3, \end{equation}
\begin{equation} \bigg|\mathbb{E}_{x,y,h,k}\prod_{\omega\in\{0,1\}^2}g_\omega((x,y)+\omega\cdot((0,h),(0,k)))\bigg|\geq \tau\alpha\beta^4\gamma^4\delta^4\rho^3, \end{equation}
where ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$ or
$T$ or ![]() $g_S$ for all
$g_S$ for all ![]() $\omega \in \{0,1\}^2$, at least one
$\omega \in \{0,1\}^2$, at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $g_S$, and at least one
$g_S$, and at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$, then
$T$, then
If
 \begin{equation} \bigg|\mathbb{E}_{x,y,h,k}\prod_{\omega\in\{0,1\}^2}g_\omega((x,y)+ \omega\cdot((h,0),(0,k)))\bigg|\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4, \end{equation}
\begin{equation} \bigg|\mathbb{E}_{x,y,h,k}\prod_{\omega\in\{0,1\}^2}g_\omega((x,y)+ \omega\cdot((h,0),(0,k)))\bigg|\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4, \end{equation}
where ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$ or
$T$ or ![]() $g_S$ for all
$g_S$ for all ![]() $\omega \in \{0,1\}^2$, at least one
$\omega \in \{0,1\}^2$, at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $g_S$, and at least one
$g_S$, and at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$, then
$T$, then
or
If
 \begin{equation} \bigg|\mathbb{E}_{x,y,h,k}\prod_{\omega\in\{0,1\}^2}g_\omega((x,y)+\omega\cdot((0,h),(-k,k)))\bigg|\geq \tau\alpha^2\beta^4\gamma^2\delta^4\rho^4, \end{equation}
\begin{equation} \bigg|\mathbb{E}_{x,y,h,k}\prod_{\omega\in\{0,1\}^2}g_\omega((x,y)+\omega\cdot((0,h),(-k,k)))\bigg|\geq \tau\alpha^2\beta^4\gamma^2\delta^4\rho^4, \end{equation}
where ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$ or
$T$ or ![]() $g_S$ for all
$g_S$ for all ![]() $\omega \in \{0,1\}^2$, at least one
$\omega \in \{0,1\}^2$, at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $g_S$, and at least one
$g_S$, and at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$, then
$T$, then
or
Proof. We rewrite the various assumptions that (31), (32), and (33) hold when at least two of the ![]() $g_\omega$ equal
$g_\omega$ equal ![]() $T$ as
$T$ as
 \begin{align*}
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_1(x,y,h)|&\geq\tau\alpha\beta^4\gamma^4\delta^4\rho^3,\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_2(x,y)|&\geq\tau\alpha\beta^4\gamma^4\delta^4\rho^3,\\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x,y+k)\mu_3(x,y,k)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y)\mu_4(x,y,h)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_5(x,y)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_6(x,y,h)|&\geq\tau\alpha^2\beta^4\gamma^2\delta^4\rho^4,\\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x-k,y+k)\mu_7(x,y,k)|&\geq\tau\alpha^2\beta^4\gamma^2\delta^4\rho^4,
\end{align*}
\begin{align*}
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_1(x,y,h)|&\geq\tau\alpha\beta^4\gamma^4\delta^4\rho^3,\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_2(x,y)|&\geq\tau\alpha\beta^4\gamma^4\delta^4\rho^3,\\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x,y+k)\mu_3(x,y,k)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y)\mu_4(x,y,h)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_5(x,y)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_6(x,y,h)|&\geq\tau\alpha^2\beta^4\gamma^2\delta^4\rho^4,\\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x-k,y+k)\mu_7(x,y,k)|&\geq\tau\alpha^2\beta^4\gamma^2\delta^4\rho^4,
\end{align*}
and
where
 \begin{align*}
\mu_1(x,y,h)&=\mathbb{E}_{k}T(x,y+k)T(x,y+h+k),\\
\mu_2(x,y)&=\mathbb{E}_{h,k}T(x,y+h)T(x,y+k)T(x,y+h+k),\\
\mu_3(x,y,k)&=\mathbb{E}_{h}T(x+h,y)T(x+h,y+k),\\
\mu_4(x,y,h)&=\mathbb{E}_{k}T(x,y+k)T(x+h,y+k),\\
\mu_5(x,y)&=\mathbb{E}_{h,k}T(x+h,y)T(x,y+k)T(x+h,y+k),\\
\mu_6(x,y,h)&=\mathbb{E}_{k}T(x-k,y+k)T(x-k,y+h+k),\\
\mu_7(x,y,k)&=\mathbb{E}_{h}T(x,y+h)T(x-k,y+h+k),
\end{align*}
\begin{align*}
\mu_1(x,y,h)&=\mathbb{E}_{k}T(x,y+k)T(x,y+h+k),\\
\mu_2(x,y)&=\mathbb{E}_{h,k}T(x,y+h)T(x,y+k)T(x,y+h+k),\\
\mu_3(x,y,k)&=\mathbb{E}_{h}T(x+h,y)T(x+h,y+k),\\
\mu_4(x,y,h)&=\mathbb{E}_{k}T(x,y+k)T(x+h,y+k),\\
\mu_5(x,y)&=\mathbb{E}_{h,k}T(x+h,y)T(x,y+k)T(x+h,y+k),\\
\mu_6(x,y,h)&=\mathbb{E}_{k}T(x-k,y+k)T(x-k,y+h+k),\\
\mu_7(x,y,k)&=\mathbb{E}_{h}T(x,y+h)T(x-k,y+h+k),
\end{align*}
and
Using the definition (11) of ![]() $T$ and arguing as in § 5 using Lemmas 3.5, 3.6, and 4.1 gives that each of
$T$ and arguing as in § 5 using Lemmas 3.5, 3.6, and 4.1 gives that each of ![]() $\mu _1,\ldots,\mu _8$ is typically very close to its average value on its support. Precisely, we have the estimates
$\mu _1,\ldots,\mu _8$ is typically very close to its average value on its support. Precisely, we have the estimates
 \begin{align*}
\mathbb{E}_{x,y,h}A(x)\Phi(x,h-u)|\mu_1(x,y,h)-\beta^2\gamma^2\delta^2\rho|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y}A(x)\Phi(x,y)|\mu_2(x,y)-\beta^3\gamma^3\delta^3\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,k}B(y)B(y+k)|\mu_3(x,y,k)-\alpha\gamma^2\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,h}A(x)A(x+h)|\mu_4(x,y,h)-\beta\gamma^2\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y}A(x)B(y)|\mu_5(x,y)-\beta^2\gamma^3\delta^3\rho^3|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,h}C(x+y)C(x+y+h)|\mu_6(x,y,h)-\alpha\beta^2\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,k}A(x)A(x-k)|\mu_7(x,y,k)-\beta^2\gamma\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},
\end{align*}
\begin{align*}
\mathbb{E}_{x,y,h}A(x)\Phi(x,h-u)|\mu_1(x,y,h)-\beta^2\gamma^2\delta^2\rho|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y}A(x)\Phi(x,y)|\mu_2(x,y)-\beta^3\gamma^3\delta^3\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,k}B(y)B(y+k)|\mu_3(x,y,k)-\alpha\gamma^2\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,h}A(x)A(x+h)|\mu_4(x,y,h)-\beta\gamma^2\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y}A(x)B(y)|\mu_5(x,y)-\beta^2\gamma^3\delta^3\rho^3|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,h}C(x+y)C(x+y+h)|\mu_6(x,y,h)-\alpha\beta^2\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\
\mathbb{E}_{x,y,k}A(x)A(x-k)|\mu_7(x,y,k)-\beta^2\gamma\delta^2\rho^2|^2&\ll\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},
\end{align*}
and
which imply that
 \begin{align*}
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_1(x,y,h)|&=\beta^2\gamma^2\delta^2\rho
\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_2(x,y)|&=\beta^3\gamma^3\delta^3\rho^2
|\mathbb{E}_{x,y}g_S(x,y)|+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg), \\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x,y+k)\mu_3(x,y,k)|&=\alpha\gamma^2\delta^2
\rho^2\mathbb{E}_{x,y,k}g_S(x,y)g_S(x,y+k)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y)\mu_4(x,y,h)|&=\beta\gamma^2\delta^2\rho^2
\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_5(x,y)|&=\beta^2\gamma^3\delta^3\rho^3
|\mathbb{E}_{x,y}g_S(x,y)|+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_6(x,y,h)|&=\alpha\beta^2\delta^2
\rho^2\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x-k,y+k)\mu_7(x,y,k)|&=\beta^2\gamma\delta^2\rho^2
\mathbb{E}_{x,y,k}g_S(x,y)g_S(x-k,y+k)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),
\end{align*}
\begin{align*}
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_1(x,y,h)|&=\beta^2\gamma^2\delta^2\rho
\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_2(x,y)|&=\beta^3\gamma^3\delta^3\rho^2
|\mathbb{E}_{x,y}g_S(x,y)|+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg), \\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x,y+k)\mu_3(x,y,k)|&=\alpha\gamma^2\delta^2
\rho^2\mathbb{E}_{x,y,k}g_S(x,y)g_S(x,y+k)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y)\mu_4(x,y,h)|&=\beta\gamma^2\delta^2\rho^2
\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y}g_S(x,y)\mu_5(x,y)|&=\beta^2\gamma^3\delta^3\rho^3
|\mathbb{E}_{x,y}g_S(x,y)|+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)\mu_6(x,y,h)|&=\alpha\beta^2\delta^2
\rho^2\mathbb{E}_{x,y,h}g_S(x,y)g_S(x,y+h)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\
|\mathbb{E}_{x,y,k}g_S(x,y)g_S(x-k,y+k)\mu_7(x,y,k)|&=\beta^2\gamma\delta^2\rho^2
\mathbb{E}_{x,y,k}g_S(x,y)g_S(x-k,y+k)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),
\end{align*}
and
Since ![]() $|\mathbb {E}_{x,y}g_S(x,y)|^2\leq \alpha \mathbb {E}_{x,y,h}g_S(x,y)g_S(x,y+h)$ by an application of the Cauchy–Schwarz inequality, the conclusion of the lemma easily follows starting from any one of the assumptions (31), (32), or (33) when at least two of the
$|\mathbb {E}_{x,y}g_S(x,y)|^2\leq \alpha \mathbb {E}_{x,y,h}g_S(x,y)g_S(x,y+h)$ by an application of the Cauchy–Schwarz inequality, the conclusion of the lemma easily follows starting from any one of the assumptions (31), (32), or (33) when at least two of the ![]() $g_\omega$ equal
$g_\omega$ equal ![]() $T$.
$T$.
To prove the lemma when only one ![]() $g_\omega$ in (31), (32), or (33) equals
$g_\omega$ in (31), (32), or (33) equals ![]() $T$, we will apply the Cauchy–Schwarz inequality once, and then argue analogously. By making a change of variables, we may start from the assumption that
$T$, we will apply the Cauchy–Schwarz inequality once, and then argue analogously. By making a change of variables, we may start from the assumption that
 \begin{align*}
|\mathbb{E}_{x,y,h,k}g_S(x,y)g_S(x,y+h)g_S(x,y+k)T(x,y+h+k)|&\geq\tau\alpha\beta^4\gamma^4\delta^4\rho^3,\\
|\mathbb{E}_{x,y,h,k}g_S(x,y)g_S(x+h,y)g_S(x,y+k)T(x+h,y+k)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,
\end{align*}
\begin{align*}
|\mathbb{E}_{x,y,h,k}g_S(x,y)g_S(x,y+h)g_S(x,y+k)T(x,y+h+k)|&\geq\tau\alpha\beta^4\gamma^4\delta^4\rho^3,\\
|\mathbb{E}_{x,y,h,k}g_S(x,y)g_S(x+h,y)g_S(x,y+k)T(x+h,y+k)|&\geq\tau\alpha^2\beta^2\gamma^4\delta^4\rho^4,
\end{align*}
or
We apply the Cauchy–Schwarz inequality in each of these three cases to get that
times ![]() $\mathbb {E}_{x,y,h}\Delta _{(0,h)}T(x,y)$ is at least
$\mathbb {E}_{x,y,h}\Delta _{(0,h)}T(x,y)$ is at least ![]() $\tau ^2\alpha ^2\beta ^8\gamma ^8\delta ^8\rho ^6$,
$\tau ^2\alpha ^2\beta ^8\gamma ^8\delta ^8\rho ^6$,
times ![]() $\mathbb {E}_{x,y,h}\Delta _{(h,0)}T(x,y)$ is at least
$\mathbb {E}_{x,y,h}\Delta _{(h,0)}T(x,y)$ is at least ![]() $\tau ^2\alpha ^4\beta ^4\gamma ^8\delta ^8\rho ^8$, or
$\tau ^2\alpha ^4\beta ^4\gamma ^8\delta ^8\rho ^8$, or
times ![]() $\mathbb {E}_{x,y,h}\Delta _{(0,h)}T(x,y)$ is at least
$\mathbb {E}_{x,y,h}\Delta _{(0,h)}T(x,y)$ is at least ![]() $\tau ^2\alpha ^4\beta ^8\gamma ^4\delta ^8\rho ^8$.
$\tau ^2\alpha ^4\beta ^8\gamma ^4\delta ^8\rho ^8$.
We have
and
by Lemmas 3.5, 3.6, and 4.1. Expanding the square and making a change of variables, (34) equals
where
(35) equals
where
and (36) equals
where
Analogously to the weights ![]() $\mu _1,\ldots,\mu _8$, Lemmas 3.5, 3.6, and 4.1 give the estimates
$\mu _1,\ldots,\mu _8$, Lemmas 3.5, 3.6, and 4.1 give the estimates
 \begin{gather*} \mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}\Phi(x,y)|\mu_9(x,y,\ell)-\beta^4\gamma^4\delta^4\rho^2|^2\ll \frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\ \mathbb{E}_{x,y,\ell}A(x)\Delta_{\ell}B(y)|\mu_{10}(x,y,\ell)-\alpha\beta\gamma^4\delta^4\rho^4|^2\ll \frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}, \end{gather*}
\begin{gather*} \mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}\Phi(x,y)|\mu_9(x,y,\ell)-\beta^4\gamma^4\delta^4\rho^2|^2\ll \frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}},\\ \mathbb{E}_{x,y,\ell}A(x)\Delta_{\ell}B(y)|\mu_{10}(x,y,\ell)-\alpha\beta\gamma^4\delta^4\rho^4|^2\ll \frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}, \end{gather*}
and
from which it follows that
 \begin{gather*} |\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)\mu_9(x,y,\ell)|= \beta^4\gamma^4\delta^4\rho^2\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)+O \bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\ |\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)\mu_{10}(x,y,\ell)|= \alpha\beta\gamma^4\delta^4\rho^4\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)+ O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg), \end{gather*}
\begin{gather*} |\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)\mu_9(x,y,\ell)|= \beta^4\gamma^4\delta^4\rho^2\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)+O \bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg),\\ |\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)\mu_{10}(x,y,\ell)|= \alpha\beta\gamma^4\delta^4\rho^4\mathbb{E}_{x,y,\ell}\Delta_{(0,\ell)}g_S(x,y)+ O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg), \end{gather*}
and
This completes the proof of the lemma.
Now we are almost ready to prove our desired density-increment result for the localized degree ![]() $2$ directional uniformity norms controlled by
$2$ directional uniformity norms controlled by ![]() $\|\cdot \|_{\star _1}$.
$\|\cdot \|_{\star _1}$.
Lemma 6.5 There exist absolute constants ![]() $0< c_1<1< c_2,c_3$ such that the following holds. Let
$0< c_1<1< c_2,c_3$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\tau >0$ and
$\tau >0$ and
and assume that
Define ![]() $T$ by (11), and let
$T$ by (11), and let ![]() $S\subset T$ have density
$S\subset T$ have density ![]() $\sigma$ in
$\sigma$ in ![]() $T$. Suppose that
$T$. Suppose that
or
Then ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\tau ^{O(1)})$ on some subset
$\sigma +\Omega (\tau ^{O(1)})$ on some subset ![]() $T'$ of
$T'$ of ![]() $T$ of the form
$T$ of the form
where the densities of ![]() $A',B'\subset \mathbb {F}_p^n$ are both
$A',B'\subset \mathbb {F}_p^n$ are both ![]() $\Omega ((\sigma \tau \alpha \beta \gamma \delta \rho )^{O(1)})$, and
$\Omega ((\sigma \tau \alpha \beta \gamma \delta \rho )^{O(1)})$, and ![]() $\Phi '$ is of the form
$\Phi '$ is of the form
where each ![]() $V_x'$ is a subspace of
$V_x'$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d+1$.
$d+1$.
To prove this lemma starting from the assumption (37), we will apply a localized ![]() $U^2(\Phi (x,\cdot ))$-norm inverse theorem for many fixed
$U^2(\Phi (x,\cdot ))$-norm inverse theorem for many fixed ![]() $x$, which will produce a density increment on a set of the form
$x$, which will produce a density increment on a set of the form
where
This is not yet what the conclusion of the lemma promises, since ![]() $u'_x$ varies with
$u'_x$ varies with ![]() $x$. To show that we can select a fixed
$x$. To show that we can select a fixed ![]() $u'$ (at the cost of shrinking the size of
$u'$ (at the cost of shrinking the size of ![]() $A'$ a bit) we will need Lemma 6.6.
$A'$ a bit) we will need Lemma 6.6.
The reader may wonder why we cannot just run the density-increment argument on sets of the form (39) and skip having to prove Lemma 6.6. The issue with this hypothetical proof is that ![]() $U^s(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-uniformity of a set of the form
$U^s(\mathbb {F}_p^n\times \mathbb {F}_p^n)$-uniformity of a set of the form ![]() $\Psi$ is not strong enough to guarantee that the analogue of Lemma 4.1 is true, regardless of how large
$\Psi$ is not strong enough to guarantee that the analogue of Lemma 4.1 is true, regardless of how large ![]() $s$ is taken to be. Thus, such sets are not as amenable to a Shkredov-like pseudorandomization procedure.
$s$ is taken to be. Thus, such sets are not as amenable to a Shkredov-like pseudorandomization procedure.
Lemma 6.6 There exist absolute constants ![]() $0< c_1<1< c_2$ such that the following holds. Let
$0< c_1<1< c_2$ such that the following holds. Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Let
$\rho :=p^{-d}$. Let ![]() $A\subset \mathbb {F}_p^n$ have density
$A\subset \mathbb {F}_p^n$ have density ![]() $\alpha$,
$\alpha$, ![]() $\Psi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ take the form
$\Psi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ take the form
where ![]() $u_{x}\in \mathbb {F}_p^n$ and each
$u_{x}\in \mathbb {F}_p^n$ and each ![]() $V_{x}$ is a subspace of
$V_{x}$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$, and
$d$, and ![]() $K\subset A\times \mathbb {F}_p^n$ satisfy
$K\subset A\times \mathbb {F}_p^n$ satisfy
for every ![]() $x\in A$ and every affine subspace
$x\in A$ and every affine subspace ![]() $H$ of
$H$ of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\tau >0$, assume that
$\tau >0$, assume that ![]() $\varepsilon \leq c_1(\tau \alpha \beta \gamma \delta \rho )^{c_2}$, and suppose that
$\varepsilon \leq c_1(\tau \alpha \beta \gamma \delta \rho )^{c_2}$, and suppose that ![]() $S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has density at least
$S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has density at least ![]() $\sigma +\tau$ in
$\sigma +\tau$ in ![]() $K\cap \Psi$, where
$K\cap \Psi$, where ![]() $\sigma >0$. Then there exists a
$\sigma >0$. Then there exists a ![]() $u\in \mathbb {F}_p^n$ and a subset
$u\in \mathbb {F}_p^n$ and a subset ![]() $A'\subset A$ such that
$A'\subset A$ such that ![]() $S\cap T'$ has density at least
$S\cap T'$ has density at least ![]() $\sigma +\tau /4$ in
$\sigma +\tau /4$ in ![]() $T'$, where
$T'$, where
 \begin{gather*} T':=A'\times\mathbb{F}_p^n\cap K\cap\Phi',\\ \Phi':=\{(x,y)\in A'\times\mathbb{F}_p^n:y\in u+V_{x}\}, \end{gather*}
\begin{gather*} T':=A'\times\mathbb{F}_p^n\cap K\cap\Phi',\\ \Phi':=\{(x,y)\in A'\times\mathbb{F}_p^n:y\in u+V_{x}\}, \end{gather*}
and ![]() $\mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(A')\geq \alpha \rho \tau /2$.
$\mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(A')\geq \alpha \rho \tau /2$.
Proof. Define
and
for every ![]() $u\in \mathbb {F}_p^n$, and set
$u\in \mathbb {F}_p^n$, and set ![]() $\alpha _{u}:=\mu _{\mathbb {F}_p^n}(A_{u})$, so that
$\alpha _{u}:=\mu _{\mathbb {F}_p^n}(A_{u})$, so that ![]() $\mathbb {E}_u\alpha _u=\alpha \rho$. By our assumption on
$\mathbb {E}_u\alpha _u=\alpha \rho$. By our assumption on ![]() $K$, we have
$K$, we have
and
for all ![]() $u\in \mathbb {F}_p^n$.
$u\in \mathbb {F}_p^n$.
Note that
and set
 \[ G(u):=\frac{\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(S\cap K\cap\Psi_{u})}{\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(K\cap\Psi_{u})} \]
\[ G(u):=\frac{\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(S\cap K\cap\Psi_{u})}{\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(K\cap\Psi_{u})} \]
for each ![]() $u\in \mathbb {F}_p^n$. Then we have
$u\in \mathbb {F}_p^n$. Then we have
 \begin{align*} (\sigma+\tau)\alpha\kappa\rho^2+O(\varepsilon)&\leq\kappa\rho\mathbb{E}_{u}\alpha_{u}G(u) \\ &<\frac{\kappa\rho}{p^n}\bigg(\bigg(\sigma+\frac{\tau}{4}\bigg)\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)<\sigma+\tau/4}}\alpha_{u}+\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)\geq\sigma+\tau/4}}\alpha_u\bigg) \\ &<\kappa\rho\bigg(\bigg(\sigma+\frac{\tau}{4}\bigg)(\alpha\rho-\eta)+\eta\bigg), \end{align*}
\begin{align*} (\sigma+\tau)\alpha\kappa\rho^2+O(\varepsilon)&\leq\kappa\rho\mathbb{E}_{u}\alpha_{u}G(u) \\ &<\frac{\kappa\rho}{p^n}\bigg(\bigg(\sigma+\frac{\tau}{4}\bigg)\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)<\sigma+\tau/4}}\alpha_{u}+\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)\geq\sigma+\tau/4}}\alpha_u\bigg) \\ &<\kappa\rho\bigg(\bigg(\sigma+\frac{\tau}{4}\bigg)(\alpha\rho-\eta)+\eta\bigg), \end{align*}
where
 \[ \eta:=\frac{1}{p^n}\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)\geq\sigma+\tau/4}}\alpha_u, \]
\[ \eta:=\frac{1}{p^n}\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)\geq\sigma+\tau/4}}\alpha_u, \]
so that
when ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough. The contribution to
$c_2$ is large enough. The contribution to ![]() $\eta$ coming from
$\eta$ coming from ![]() $u$ for which
$u$ for which ![]() $\alpha _u<\tau \alpha \rho /2$ is obviously at most
$\alpha _u<\tau \alpha \rho /2$ is obviously at most ![]() $\tau \alpha \rho /2$, which implies that
$\tau \alpha \rho /2$, which implies that
 \[ \frac{1}{p^n}\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)\geq\sigma+\tau/4 \\ \alpha_u\geq\tau\alpha\rho/2}}\alpha_u>\frac{\tau\alpha\rho}{8}, \]
\[ \frac{1}{p^n}\sum_{\substack{ u\in\mathbb{F}_p^n \\ G(u)\geq\sigma+\tau/4 \\ \alpha_u\geq\tau\alpha\rho/2}}\alpha_u>\frac{\tau\alpha\rho}{8}, \]
which is clearly positive. We thus conclude that there must exist a ![]() $u\in \mathbb {F}_p^n$ for which
$u\in \mathbb {F}_p^n$ for which ![]() $\alpha _u=\mu _{\mathbb {F}_p^n}(A_{u})\geq \tau \alpha \rho /2$ and
$\alpha _u=\mu _{\mathbb {F}_p^n}(A_{u})\geq \tau \alpha \rho /2$ and
The conclusion of the lemma now follows by taking ![]() $A'=A_{u}$ and
$A'=A_{u}$ and ![]() $\Phi '=\Psi _{u}\cap (A'\times \mathbb {F}_p^n)$.
$\Phi '=\Psi _{u}\cap (A'\times \mathbb {F}_p^n)$.
Now we can prove Lemma 6.5.
Proof of Lemma 6.5 First assume that (37) holds. By writing ![]() $S=g_S+\sigma T$, we see that
$S=g_S+\sigma T$, we see that ![]() $\mathbb {E}_{x,y,h,k}\Delta _{(0,h),(0,k)}S(x,y)$ equals
$\mathbb {E}_{x,y,h,k}\Delta _{(0,h),(0,k)}S(x,y)$ equals
plus ![]() $14$ terms of the form
$14$ terms of the form
where at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $g_S$ and at least one other equals
$g_S$ and at least one other equals ![]() $\sigma T$, and
$\sigma T$, and
If one of the terms (40) has absolute value larger than ![]() $\tau \alpha \beta ^4\gamma ^4\delta ^4\rho ^3/32$, then combining Lemmas 6.4 and 6.3 produces the desired density increment. Thus, we may proceed under the assumption that all have size at most
$\tau \alpha \beta ^4\gamma ^4\delta ^4\rho ^3/32$, then combining Lemmas 6.4 and 6.3 produces the desired density increment. Thus, we may proceed under the assumption that all have size at most ![]() $\tau \alpha \beta ^4\gamma ^4\delta ^4\rho ^3/32$, so that
$\tau \alpha \beta ^4\gamma ^4\delta ^4\rho ^3/32$, so that
For each ![]() $x\in \mathbb {F}_p^n$, set
$x\in \mathbb {F}_p^n$, set ![]() $\Phi _x(y):=\Phi (x,y)$,
$\Phi _x(y):=\Phi (x,y)$, ![]() $T_x(y):=T(x,y)$, and
$T_x(y):=T(x,y)$, and ![]() $S_x(y)=S(x,y)$. Lemmas 3.5, 3.6, and 4.1 tell us that
$S_x(y)=S(x,y)$. Lemmas 3.5, 3.6, and 4.1 tell us that
 \begin{gather*} \mathbb{E}_xA(x)|\mathbb{E}_{y,h,k}\Delta_{h,k}T_x(y)-\beta^4\gamma^4\delta^4\rho^3|\ll\varepsilon^{\Omega(1)},\\ \mathbb{E}_{x}A(x)\|T_x-\beta\gamma\delta\|_{U^2(\Phi_x)}^4\ll\varepsilon^{\Omega(1)}, \end{gather*}
\begin{gather*} \mathbb{E}_xA(x)|\mathbb{E}_{y,h,k}\Delta_{h,k}T_x(y)-\beta^4\gamma^4\delta^4\rho^3|\ll\varepsilon^{\Omega(1)},\\ \mathbb{E}_{x}A(x)\|T_x-\beta\gamma\delta\|_{U^2(\Phi_x)}^4\ll\varepsilon^{\Omega(1)}, \end{gather*}
and that
or else Lemma 6.3 will again give the desired density increment. It follows that there exists a subset ![]() $A_0\subset A$ of density
$A_0\subset A$ of density ![]() $\gg \tau$ in
$\gg \tau$ in ![]() $A$ such that
$A$ such that
and
for every ![]() $x\in A_0$. Setting
$x\in A_0$. Setting
for all ![]() $x\in A_0$ we then have
$x\in A_0$ we then have ![]() $\|f_x\|^4_{U^2(\Phi _x)}\geq \sigma ^4+\tau /4$,
$\|f_x\|^4_{U^2(\Phi _x)}\geq \sigma ^4+\tau /4$, ![]() $0\leq f_x\leq \nu _x$,
$0\leq f_x\leq \nu _x$, ![]() $\mathbb {E}_{y}f_x(y)\leq 1$, and
$\mathbb {E}_{y}f_x(y)\leq 1$, and
provided that ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough. Thus, as long as
$c_2$ is large enough. Thus, as long as ![]() $c_3$ is sufficiently large, Lemma 6.1 tells us that there exists a function
$c_3$ is sufficiently large, Lemma 6.1 tells us that there exists a function ![]() $\tilde {f}_x:\Phi _x\to [0,1]$ such that
$\tilde {f}_x:\Phi _x\to [0,1]$ such that ![]() $\mathbb {E}_{y\in \Phi _x}f_x(y)=\mathbb {E}_{y\in \Phi _x}\tilde {f}_x(y)$ and
$\mathbb {E}_{y\in \Phi _x}f_x(y)=\mathbb {E}_{y\in \Phi _x}\tilde {f}_x(y)$ and ![]() $\|f_x-\tilde {f}_x\|_{U^2(\Phi _x)}^4\leq \tau /32$. As a consequence, since
$\|f_x-\tilde {f}_x\|_{U^2(\Phi _x)}^4\leq \tau /32$. As a consequence, since ![]() $\|f_x\|^4_{U^2(\Phi _x)}\geq \sigma ^4+ {\tau }/{4}$, we must have
$\|f_x\|^4_{U^2(\Phi _x)}\geq \sigma ^4+ {\tau }/{4}$, we must have
as well. Set ![]() $\tilde {\sigma }_x:=\mathbb {E}_{y}f_x(y)=\mathbb {E}_{y}\tilde {f}_x(y)$ and let
$\tilde {\sigma }_x:=\mathbb {E}_{y}f_x(y)=\mathbb {E}_{y}\tilde {f}_x(y)$ and let ![]() $v_x\in \Phi _x$, so that
$v_x\in \Phi _x$, so that
 \[ \|\tilde{f}_x\|_{U^2(\Phi_x)}^4=\tilde{\sigma}_x^4+ \sum_{0\neq\xi\in\widehat{\Phi_x-v_x}}|(\widehat{\tilde{f}_x-\tilde{\sigma}})(\xi)|^4. \]
\[ \|\tilde{f}_x\|_{U^2(\Phi_x)}^4=\tilde{\sigma}_x^4+ \sum_{0\neq\xi\in\widehat{\Phi_x-v_x}}|(\widehat{\tilde{f}_x-\tilde{\sigma}})(\xi)|^4. \]
Since ![]() $|\tilde {\sigma }_x-\sigma |<\tau /64$, it follows that there exists a nonzero
$|\tilde {\sigma }_x-\sigma |<\tau /64$, it follows that there exists a nonzero ![]() $\xi _x\in \widehat {\Phi _x-v_x}$ such that
$\xi _x\in \widehat {\Phi _x-v_x}$ such that
where we have crucially used that ![]() $\tilde {f}_x$ is
$\tilde {f}_x$ is ![]() $1$-bounded. As
$1$-bounded. As ![]() $\|f_x-\tilde {f}_x\|_{U^2(\Phi _x)}^4\leq \tau /32$, it therefore follows that
$\|f_x-\tilde {f}_x\|_{U^2(\Phi _x)}^4\leq \tau /32$, it therefore follows that
for every ![]() $x\in A_0$.
$x\in A_0$.
Extend ![]() $x\mapsto \xi _x$ from
$x\mapsto \xi _x$ from ![]() $A_0$ to
$A_0$ to ![]() $A$ by picking a nonzero
$A$ by picking a nonzero ![]() $\xi _x\in \widehat {\Phi _x-v_x}$ arbitrarily for all
$\xi _x\in \widehat {\Phi _x-v_x}$ arbitrarily for all ![]() $x\in A\setminus A_0$. We now split the average over
$x\in A\setminus A_0$. We now split the average over ![]() $y\in \Phi _x$ above into an average of averages over cosets of
$y\in \Phi _x$ above into an average of averages over cosets of ![]() $\langle \xi _x\rangle ^\perp$ in
$\langle \xi _x\rangle ^\perp$ in ![]() $\Phi _x$ and average over all of
$\Phi _x$ and average over all of ![]() $A$ to get that
$A$ to get that
and use the fact that
to deduce that
By applying the pigeonhole principle in the ![]() $x$ and
$x$ and ![]() $t$ variables, it follows that there exists a subset
$t$ variables, it follows that there exists a subset ![]() $A_1\subset A$ of density
$A_1\subset A$ of density ![]() $\gg \tau$ in
$\gg \tau$ in ![]() $A$ and, for each
$A$ and, for each ![]() $x\in A_1$, an element
$x\in A_1$, an element ![]() $t_x\in \mathbb {F}_p$ for which
$t_x\in \mathbb {F}_p$ for which
Thus, recalling the definition of ![]() $f_x$, we have
$f_x$, we have
Define ![]() $\phi :\mathbb {F}_p^n\to \mathbb {F}_p^n$ by taking
$\phi :\mathbb {F}_p^n\to \mathbb {F}_p^n$ by taking ![]() $\phi (x)=\xi _x$ for all
$\phi (x)=\xi _x$ for all ![]() $x\in A$ and
$x\in A$ and ![]() $\phi (x)$ to be an arbitrary element of
$\phi (x)$ to be an arbitrary element of ![]() $(\Phi _x-v_x)^\perp \setminus \{0\}$ for all
$(\Phi _x-v_x)^\perp \setminus \{0\}$ for all ![]() $x\in \mathbb {F}_p^n\setminus A$, and similarly extend
$x\in \mathbb {F}_p^n\setminus A$, and similarly extend ![]() $x\mapsto t_x$ from
$x\mapsto t_x$ from ![]() $A_1$ to
$A_1$ to ![]() $A$ by taking
$A$ by taking ![]() $t_x$ to be an arbitrary element of
$t_x$ to be an arbitrary element of ![]() $\mathbb {F}_p$ for which
$\mathbb {F}_p$ for which
for all ![]() $x\in A\setminus A_1$. Such an element must exist by the pigeonhole principle. Set
$x\in A\setminus A_1$. Such an element must exist by the pigeonhole principle. Set
so that ![]() $\operatorname {codim}\{y\in \mathbb {F}_p^n:\Psi (x,y)=1\}=d+1$ for every
$\operatorname {codim}\{y\in \mathbb {F}_p^n:\Psi (x,y)=1\}=d+1$ for every ![]() $x\in A$, and
$x\in A$, and ![]() $\alpha _1:=|A_1|/p^n$. Then (41) can be rewritten as
$\alpha _1:=|A_1|/p^n$. Then (41) can be rewritten as
It remains to check that the density ![]() $\mathbb {E}_{x,y}A_1(x)B(y)C(x+y)D(2x+y)\Psi (x,y)$ is close to
$\mathbb {E}_{x,y}A_1(x)B(y)C(x+y)D(2x+y)\Psi (x,y)$ is close to ![]() $\alpha _1\beta \gamma \delta \rho /p$, so that we indeed have the desired density increment. But by Lemmas 3.5 and 3.6, we have
$\alpha _1\beta \gamma \delta \rho /p$, so that we indeed have the desired density increment. But by Lemmas 3.5 and 3.6, we have
for all but a ![]() $O(\sqrt {\varepsilon })$-proportion of
$O(\sqrt {\varepsilon })$-proportion of ![]() $x\in A$, from which it follows that
$x\in A$, from which it follows that
Thus, ![]() $S$ has density at least
$S$ has density at least ![]() $\sigma +\Omega (\tau )$ on
$\sigma +\Omega (\tau )$ on
provided that ![]() $c_2$ is large enough. The conclusion of the lemma now follows from Lemma 6.6
$c_2$ is large enough. The conclusion of the lemma now follows from Lemma 6.6
Now suppose that (38) holds. By writing ![]() $S=g_S+\sigma T$ and arguing as in the first case, we may proceed under the assumption that
$S=g_S+\sigma T$ and arguing as in the first case, we may proceed under the assumption that
We will first show that either
for almost every pair ![]() $(x',y')\in S$, or else we can deduce the desired density increment using Lemma 6.3.
$(x',y')\in S$, or else we can deduce the desired density increment using Lemma 6.3.
Consider the average
Using that ![]() $S=g_S+\sigma T$, the above can be written as
$S=g_S+\sigma T$, the above can be written as
plus seven other terms of the form
where ![]() $g_0,g_1,$ and
$g_0,g_1,$ and ![]() $g_2$ all equal
$g_2$ all equal ![]() $g_S$ or
$g_S$ or ![]() $\sigma T$ and at least one
$\sigma T$ and at least one ![]() $g_i$ equals
$g_i$ equals ![]() $g_S$. By Lemmas 3.5, 3.6, and 4.1, the quantity (42) equals
$g_S$. By Lemmas 3.5, 3.6, and 4.1, the quantity (42) equals ![]() $\sigma ^3\alpha ^2\beta ^2\gamma ^4\delta ^4\rho ^4+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Suppose that
$\sigma ^3\alpha ^2\beta ^2\gamma ^4\delta ^4\rho ^4+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Suppose that ![]() $k$ of the functions
$k$ of the functions ![]() $g_0,g_1,$ and
$g_0,g_1,$ and ![]() $g_2$ in (43) equal
$g_2$ in (43) equal ![]() $\sigma T$. By a similar argument to those used to prove Lemma 6.4, if any term of the form (43) has size at least
$\sigma T$. By a similar argument to those used to prove Lemma 6.4, if any term of the form (43) has size at least ![]() $\tau ^4\sigma ^k\alpha ^2\beta ^2\gamma ^4\delta ^4\rho ^4$, then
$\tau ^4\sigma ^k\alpha ^2\beta ^2\gamma ^4\delta ^4\rho ^4$, then
or
so that the desired density increment follows from Lemma 6.3. Thus, we may proceed under the assumption that
Now consider the average
Using that ![]() $S=g_S+\sigma T$, the above can be written as
$S=g_S+\sigma T$, the above can be written as
plus 31 other terms of the form
where ![]() $g_0,g_1,g_2,g_3,$ and
$g_0,g_1,g_2,g_3,$ and ![]() $g_4$ all equal
$g_4$ all equal ![]() $g_S$ or
$g_S$ or ![]() $\sigma T$ and at least one
$\sigma T$ and at least one ![]() $g_i$ equals
$g_i$ equals ![]() $g_S$.
$g_S$.
By Lemmas 3.5, 3.6, and 4.1, the quantity (44) equals ![]() $\sigma ^5\alpha ^3\beta ^3\gamma ^7\delta ^7\rho ^7+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Suppose that
$\sigma ^5\alpha ^3\beta ^3\gamma ^7\delta ^7\rho ^7+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Suppose that ![]() $k$ of the functions
$k$ of the functions ![]() $g_0,\ldots,g_4$ in (45) equal
$g_0,\ldots,g_4$ in (45) equal ![]() $\sigma T$. Analogously to the situation for the first moment, if any of the terms of the form (45) has size at least
$\sigma T$. Analogously to the situation for the first moment, if any of the terms of the form (45) has size at least ![]() $\tau ^8\sigma ^k\alpha ^3\beta ^3\gamma ^7\delta ^7\rho ^7$, then we will be able to deduce the desired density increment. The most involved case is when
$\tau ^8\sigma ^k\alpha ^3\beta ^3\gamma ^7\delta ^7\rho ^7$, then we will be able to deduce the desired density increment. The most involved case is when ![]() $g_0=\cdots =g_4=g_S$. All other cases can be handled using a simpler version of the argument we are about to carry out.
$g_0=\cdots =g_4=g_S$. All other cases can be handled using a simpler version of the argument we are about to carry out.
Thus, consider this most involved case, i.e. that
has size at least ![]() $\tau ^8\alpha ^3\beta ^3\gamma ^7\delta ^7\rho ^7$. Applying the Cauchy–Schwarz inequality in the variables
$\tau ^8\alpha ^3\beta ^3\gamma ^7\delta ^7\rho ^7$. Applying the Cauchy–Schwarz inequality in the variables ![]() $x',y',y,$ and
$x',y',y,$ and ![]() $w$ gives that
$w$ gives that
times
 \begin{align*} \mathbb{E}_{x',y',y,w}(&|\mathbb{E}_{x,z}g_S(x,y')g_S(z,y')C(x+y)C(z+w)D(2x+w)D(2z+w)\Phi(x,y)\Phi(z,w)|^2 \\ &\cdot B(y)B(w)C(x'+y')C(x'+y)C(x'+w) \\ &\cdot D(2x'+y')D(2x'+y)D(2x'+w)\Phi(x',y')\Phi(x',y)\Phi(x',w)) \end{align*}
\begin{align*} \mathbb{E}_{x',y',y,w}(&|\mathbb{E}_{x,z}g_S(x,y')g_S(z,y')C(x+y)C(z+w)D(2x+w)D(2z+w)\Phi(x,y)\Phi(z,w)|^2 \\ &\cdot B(y)B(w)C(x'+y')C(x'+y)C(x'+w) \\ &\cdot D(2x'+y')D(2x'+y)D(2x'+w)\Phi(x',y')\Phi(x',y)\Phi(x',w)) \end{align*}
is at least ![]() $\tau ^8\alpha ^{6}\beta ^{6}\gamma ^{14}\delta ^{14}\rho ^{14}$. By Lemmas 3.5, 3.6, and 4.1,
$\tau ^8\alpha ^{6}\beta ^{6}\gamma ^{14}\delta ^{14}\rho ^{14}$. By Lemmas 3.5, 3.6, and 4.1, ![]() $\mathbb {E}_{x',y',y,w}T(x',y')T(x',y)T(x',w)=\alpha \beta ^3\gamma ^3\delta ^3\rho ^3+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Expanding the square in the average above, this means that
$\mathbb {E}_{x',y',y,w}T(x',y')T(x',y)T(x',w)=\alpha \beta ^3\gamma ^3\delta ^3\rho ^3+O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$. Expanding the square in the average above, this means that
 \begin{align*} \mathbb{E}_{x',y',y,w,x,z,u,v}(&g_S(x,y')g_S(z,y')g_S(u,y')g_S(v,y') \\ &B(y)B(w)C(x'+y')C(x'+y)C(x'+w) \\ &C(x+y)C(z+w)C(u+y)C(v+w) \\ &D(2x+w)D(2z+w)D(2u+w)D(2v+w) \\ &D(2x'+y')D(2x'+y)D(2x'+w) \\ &\Phi(x,y)\Phi(z,w)\Phi(u,y)\Phi(v,w)\Phi(x',y')\Phi(x',y)\Phi(x',w)) \end{align*}
\begin{align*} \mathbb{E}_{x',y',y,w,x,z,u,v}(&g_S(x,y')g_S(z,y')g_S(u,y')g_S(v,y') \\ &B(y)B(w)C(x'+y')C(x'+y)C(x'+w) \\ &C(x+y)C(z+w)C(u+y)C(v+w) \\ &D(2x+w)D(2z+w)D(2u+w)D(2v+w) \\ &D(2x'+y')D(2x'+y)D(2x'+w) \\ &\Phi(x,y)\Phi(z,w)\Phi(u,y)\Phi(v,w)\Phi(x',y')\Phi(x',y)\Phi(x',w)) \end{align*}
is ![]() $\gg \tau ^8\alpha ^5\beta ^3\gamma ^{11}\delta ^{11}\rho ^{11}$, provided that
$\gg \tau ^8\alpha ^5\beta ^3\gamma ^{11}\delta ^{11}\rho ^{11}$, provided that ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough. We can write the above as
$c_2$ is large enough. We can write the above as
where
 \begin{align*} \mu(y',x,z,u,v):=\mathbb{E}_{x',y,w}(&B(y)B(w)C(x'+y')C(x'+y)C(x'+w) \\ &C(x+y)C(z+w)C(u+y)C(v+w) \\ &D(2x+w)D(2z+w)D(2u+w)D(2v+w) \\ &D(2x'+y')D(2x'+y)D(2x'+w) \\ &\Phi(x,y)\Phi(z,w)\Phi(u,y)\Phi(v,w)\Phi(x',y')\Phi(x',y)\Phi(x',w)). \end{align*}
\begin{align*} \mu(y',x,z,u,v):=\mathbb{E}_{x',y,w}(&B(y)B(w)C(x'+y')C(x'+y)C(x'+w) \\ &C(x+y)C(z+w)C(u+y)C(v+w) \\ &D(2x+w)D(2z+w)D(2u+w)D(2v+w) \\ &D(2x'+y')D(2x'+y)D(2x'+w) \\ &\Phi(x,y)\Phi(z,w)\Phi(u,y)\Phi(v,w)\Phi(x',y')\Phi(x',y)\Phi(x',w)). \end{align*}
Yet more applications of Lemmas 3.5, 3.6, and 4.1 give the estimate
so that
It follows from one more application of the Cauchy–Schwarz inequality in the variables ![]() $y',z,u,$ and
$y',z,u,$ and ![]() $v$ and a similar analysis to above that
$v$ and a similar analysis to above that
which, combined with Lemma 6.3, gives the desired density increment.
Thus, we may also proceed under the assumption that
By Markov's inequality, we therefore have
for all but a ![]() $O(\tau ^2)$-proportion of
$O(\tau ^2)$-proportion of ![]() $(x',y')\in S$. As a consequence, there exists a pair
$(x',y')\in S$. As a consequence, there exists a pair ![]() $(x',y')\in S$ for which both (46) holds and
$(x',y')\in S$ for which both (46) holds and
which together imply that
when we take ![]() $A'(x)=S(x,y')$,
$A'(x)=S(x,y')$, ![]() $B'(y)=S(x',y)$,
$B'(y)=S(x',y)$, ![]() $C'=C$,
$C'=C$, ![]() $D'=D$, and
$D'=D$, and ![]() $\Phi '=\Phi$ in the definition of
$\Phi '=\Phi$ in the definition of ![]() $T'$.
$T'$.
6.3 More preliminaries for  $\|\cdot \|_{\star _1}$
$\|\cdot \|_{\star _1}$
We will similarly need that certain ![]() $\|\cdot \|_{\star _1}$-inner products are controlled by the degree
$\|\cdot \|_{\star _1}$-inner products are controlled by the degree ![]() $1$ and
$1$ and ![]() $2$ directional uniformity norms appearing in the previous subsections. The proof of the lemma below is similar to the proof of Lemma 6.4, but with an extra application of the Cauchy–Schwarz inequality in some cases.
$2$ directional uniformity norms appearing in the previous subsections. The proof of the lemma below is similar to the proof of Lemma 6.4, but with an extra application of the Cauchy–Schwarz inequality in some cases.
Lemma 6.7 Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\varepsilon >0$, and assume that
$\varepsilon >0$, and assume that
Define ![]() $T$ by (11), and let
$T$ by (11), and let ![]() $S\subset T$ and
$S\subset T$ and ![]() $\tau >0$. If
$\tau >0$. If
 \[ \bigg|\mathbb{E}_{x,y,h_1,h_2,h_3}\prod_{\omega\in\{0,1\}^3}g_\omega((x,y)+\omega \cdot((0,h_1),(0,h_2),(h_3,0)))\bigg|\geq\tau\alpha^2\beta^4\gamma^8\delta^8\rho^6, \]
\[ \bigg|\mathbb{E}_{x,y,h_1,h_2,h_3}\prod_{\omega\in\{0,1\}^3}g_\omega((x,y)+\omega \cdot((0,h_1),(0,h_2),(h_3,0)))\bigg|\geq\tau\alpha^2\beta^4\gamma^8\delta^8\rho^6, \]
where at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $T$ and another equals
$T$ and another equals ![]() $g_S$, then
$g_S$, then
 \begin{align*}
\mathbb{E}_{x,y,h}\Delta_{(0,h)}g_S(x,y)&\geq\tau^8\alpha\beta^2\gamma^2\delta^2
\rho^2+O\bigg(\frac{\varepsilon^{\Omega(1)}}{(\alpha\beta\gamma\delta\rho)^{O(1)}}\bigg),\\
\mathbb{E}_{x,y,h}\Delta_{(h,0)}g_S(x,y)&\geq\tau^8\alpha^2\beta\gamma^2
\delta^2\rho^2+O\bigg(\frac{\varepsilon^{\Omega(1)}}{(\alpha\beta\gamma\delta\rho)^{O(1)}}\bigg),\\
\mathbb{E}_{x,y,h,k}\Delta_{(0,h),(0,k)}g_S(x,y)&\geq\tau^8\alpha\beta^4\gamma^4\delta^4
\rho^3+O\bigg(\frac{\varepsilon^{\Omega(1)}}{(\alpha\beta\gamma\delta\rho)^{O(1)}}\bigg),
\end{align*}
\begin{align*}
\mathbb{E}_{x,y,h}\Delta_{(0,h)}g_S(x,y)&\geq\tau^8\alpha\beta^2\gamma^2\delta^2
\rho^2+O\bigg(\frac{\varepsilon^{\Omega(1)}}{(\alpha\beta\gamma\delta\rho)^{O(1)}}\bigg),\\
\mathbb{E}_{x,y,h}\Delta_{(h,0)}g_S(x,y)&\geq\tau^8\alpha^2\beta\gamma^2
\delta^2\rho^2+O\bigg(\frac{\varepsilon^{\Omega(1)}}{(\alpha\beta\gamma\delta\rho)^{O(1)}}\bigg),\\
\mathbb{E}_{x,y,h,k}\Delta_{(0,h),(0,k)}g_S(x,y)&\geq\tau^8\alpha\beta^4\gamma^4\delta^4
\rho^3+O\bigg(\frac{\varepsilon^{\Omega(1)}}{(\alpha\beta\gamma\delta\rho)^{O(1)}}\bigg),
\end{align*}
or
Our final preliminary lemma says that, for almost every ![]() $(x,x+h_3)\in A^2$, the function
$(x,x+h_3)\in A^2$, the function ![]() $\Delta _{(h_3,0)}S(x,\cdot )$ is supported on a Fourier uniform subset of the affine subspace
$\Delta _{(h_3,0)}S(x,\cdot )$ is supported on a Fourier uniform subset of the affine subspace ![]() $\{y\in \mathbb {F}_p^n:\Delta _{(h_3,0)}\Phi (x,y)=1\}$.
$\{y\in \mathbb {F}_p^n:\Delta _{(h_3,0)}\Phi (x,y)=1\}$.
Lemma 6.8 Let ![]() $d$ be a nonnegative integer, and set
$d$ be a nonnegative integer, and set ![]() $\rho :=p^{-d}$. Suppose that
$\rho :=p^{-d}$. Suppose that ![]() $A,B,C,D\subset \mathbb {F}_p^n$ have densities
$A,B,C,D\subset \mathbb {F}_p^n$ have densities ![]() $\alpha,\beta,\gamma,\delta$, respectively, and that
$\alpha,\beta,\gamma,\delta$, respectively, and that ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ takes the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension
$\mathbb {F}_p^n$ of codimension ![]() $d$. Let
$d$. Let ![]() $\varepsilon >0$, and assume that
$\varepsilon >0$, and assume that
Setting
and
then the probability
is ![]() $\ll \varepsilon ^{\Omega (1)}/\rho ^{O(1)}$.
$\ll \varepsilon ^{\Omega (1)}/\rho ^{O(1)}$.
Proof. By Lemmas 3.6 and 4.1, we have that ![]() $\|R_{x,y}-\beta \gamma ^2\delta ^2\|_{U^2(\mathbb {F}_p^n)}\geq \varepsilon ^{1/8}$ or
$\|R_{x,y}-\beta \gamma ^2\delta ^2\|_{U^2(\mathbb {F}_p^n)}\geq \varepsilon ^{1/8}$ or ![]() $\operatorname {codim}\{y\in \mathbb {F}_p^n:\Phi _{x,h}(y)=1\}\neq 2d$ for at most a
$\operatorname {codim}\{y\in \mathbb {F}_p^n:\Phi _{x,h}(y)=1\}\neq 2d$ for at most a ![]() $O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$-proportion of pairs
$O(\varepsilon ^{\Omega (1)}/\rho ^{O(1)})$-proportion of pairs ![]() $(x,x+h)\in A^2$. For all of these typical pairs
$(x,x+h)\in A^2$. For all of these typical pairs ![]() $(x,h)$, we have
$(x,h)$, we have
which is at most
 \begin{align*} \sum_{\xi,\eta,\nu\in(\Phi_{x,h}-u)^\perp} |\mathbb{E}_{y,k,\ell}&[R_{x,h}-\beta\gamma^2\delta^2](y)e_p(\xi\cdot y) [R_{x,h}-\beta\gamma^2\delta^2](y+k)e_p(\eta\cdot (y+k)) \\ & [R_{x,h}-\beta\gamma^2\delta^2](y+\ell)e_p(\nu\cdot (y+\ell)) [R_{x,h}-\beta\gamma^2\delta^2](y+k+\ell)| \end{align*}
\begin{align*} \sum_{\xi,\eta,\nu\in(\Phi_{x,h}-u)^\perp} |\mathbb{E}_{y,k,\ell}&[R_{x,h}-\beta\gamma^2\delta^2](y)e_p(\xi\cdot y) [R_{x,h}-\beta\gamma^2\delta^2](y+k)e_p(\eta\cdot (y+k)) \\ & [R_{x,h}-\beta\gamma^2\delta^2](y+\ell)e_p(\nu\cdot (y+\ell)) [R_{x,h}-\beta\gamma^2\delta^2](y+k+\ell)| \end{align*}
by inserting the identity
 \[ \Phi_{x,h}(z)=\frac{1}{p^{2d}}\sum_{\xi\in(\Phi_{x,h}-u)^\perp}e_p(\xi\cdot[z-u]) \]
\[ \Phi_{x,h}(z)=\frac{1}{p^{2d}}\sum_{\xi\in(\Phi_{x,h}-u)^\perp}e_p(\xi\cdot[z-u]) \]
for every ![]() $z\in \mathbb {F}_p^n$. For each fixed triple
$z\in \mathbb {F}_p^n$. For each fixed triple ![]() $(\xi,\eta,\nu )$, the interior average above is bounded by
$(\xi,\eta,\nu )$, the interior average above is bounded by ![]() $\|R_{x,h}-\beta \gamma ^2\delta ^2\|_{U^2(\mathbb {F}_p^n)}$ by the Gowers–Cauchy–Schwarz inequality. Since there are
$\|R_{x,h}-\beta \gamma ^2\delta ^2\|_{U^2(\mathbb {F}_p^n)}$ by the Gowers–Cauchy–Schwarz inequality. Since there are ![]() $\rho ^{-6}$ possible triples to sum over, we must have
$\rho ^{-6}$ possible triples to sum over, we must have
from which the conclusion of the lemma follows.
6.4 Proof of Theorem 2.5
Now we can finally finish the proof of Theorem 2.5.
Proof of Theorem 2.5 First assume that
Analogously to the proof of Lemma 6.5, by writing ![]() $S=g_S+\sigma T$, we see that
$S=g_S+\sigma T$, we see that ![]() $\|S\|_{\star _1}^8$ equals
$\|S\|_{\star _1}^8$ equals
plus 62 terms of the form
where at least one ![]() $g_\omega$ equals
$g_\omega$ equals ![]() $\sigma T$ and at least one other equals
$\sigma T$ and at least one other equals ![]() $g_S$. Note that
$g_S$. Note that
by Lemmas 3.5, 3.6, and 4.1. If any of the terms (47) have absolute value at least ![]() $\frac {1}{128}\tau ^8\alpha ^2\beta ^4\gamma ^8\delta ^8\rho ^6$, then combining Lemma 6.7 with Lemma 6.3 or Lemma 6.5 produces the desired density increment. We may thus proceed under the assumption that these terms are all small, so that
$\frac {1}{128}\tau ^8\alpha ^2\beta ^4\gamma ^8\delta ^8\rho ^6$, then combining Lemma 6.7 with Lemma 6.3 or Lemma 6.5 produces the desired density increment. We may thus proceed under the assumption that these terms are all small, so that
For each pair ![]() $(x,x+h)\in A^2$, let
$(x,x+h)\in A^2$, let ![]() $R_{x,h}$ and
$R_{x,h}$ and ![]() $\Phi _{x,h}$ be as in Lemma 6.8, and set
$\Phi _{x,h}$ be as in Lemma 6.8, and set ![]() $S_{x,h}(y):=\Delta _{(h,0)}S(x,y)$. By Markov's inequality, either
$S_{x,h}(y):=\Delta _{(h,0)}S(x,y)$. By Markov's inequality, either
or else ![]() $\mathbb {E}_{x,x+h\in A}|\mathbb {E}_{y}S_{x,h}(y)-\sigma ^2\beta \gamma ^2\delta ^2\rho ^2|^2$ is
$\mathbb {E}_{x,x+h\in A}|\mathbb {E}_{y}S_{x,h}(y)-\sigma ^2\beta \gamma ^2\delta ^2\rho ^2|^2$ is ![]() $\gg \tau ^{16}\beta ^2\gamma ^4\delta ^4\rho ^4$, in which case a combination of Lemmas 6.3, 6.4, and 6.5 will produce the desired density increment. We may thus proceed under the assumption that (48) holds.
$\gg \tau ^{16}\beta ^2\gamma ^4\delta ^4\rho ^4$, in which case a combination of Lemmas 6.3, 6.4, and 6.5 will produce the desired density increment. We may thus proceed under the assumption that (48) holds.
By (48) and Lemma 6.8, there exists a subset ![]() $A_0\subset \{(x,h)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:x,x+h\in A\}$ of density
$A_0\subset \{(x,h)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:x,x+h\in A\}$ of density ![]() $\gg \tau ^{O(1)}\alpha ^2$ in
$\gg \tau ^{O(1)}\alpha ^2$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ such that
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ such that
 \begin{gather*} \|S_{x,h}\|_{U^2(\Phi_{x,h})}^4\geq \bigg(\sigma^8+\frac{\tau^8}{4}\bigg)\beta^4\gamma^8\delta^8,\\ |\mathbb{E}_{y}S_{x,h}(y)-\sigma^2\beta\gamma^2\delta^2\rho^2|< \frac{\tau^8}{64}\beta\gamma^2\delta^2\rho^2,\\ \|R_{x,h}\Phi_{x,h}-\beta\gamma^2\delta^2\|_{U^2(\Phi_{x,h})}<\frac{\varepsilon^{1/32}}{\rho^{3/2}}, \end{gather*}
\begin{gather*} \|S_{x,h}\|_{U^2(\Phi_{x,h})}^4\geq \bigg(\sigma^8+\frac{\tau^8}{4}\bigg)\beta^4\gamma^8\delta^8,\\ |\mathbb{E}_{y}S_{x,h}(y)-\sigma^2\beta\gamma^2\delta^2\rho^2|< \frac{\tau^8}{64}\beta\gamma^2\delta^2\rho^2,\\ \|R_{x,h}\Phi_{x,h}-\beta\gamma^2\delta^2\|_{U^2(\Phi_{x,h})}<\frac{\varepsilon^{1/32}}{\rho^{3/2}}, \end{gather*}
and ![]() $\operatorname {codim}\{y\in \mathbb {F}_p^n:\Phi _{x,h}(y)=1\}=2d$ for all
$\operatorname {codim}\{y\in \mathbb {F}_p^n:\Phi _{x,h}(y)=1\}=2d$ for all ![]() $(x,h)\in A_0$. Note that
$(x,h)\in A_0$. Note that ![]() $S_{x,h}$ is supported on
$S_{x,h}$ is supported on ![]() $R_{x,h}\Phi _{x,h}$, and, setting
$R_{x,h}\Phi _{x,h}$, and, setting
we have ![]() $\|f_{x,h}\|^4_{U^2(\Phi _{x,h})}\geq \sigma ^8+\tau ^8/4$,
$\|f_{x,h}\|^4_{U^2(\Phi _{x,h})}\geq \sigma ^8+\tau ^8/4$, ![]() $0\leq f_{x,h}\leq \nu _{x,h}$,
$0\leq f_{x,h}\leq \nu _{x,h}$, ![]() $\mathbb {E} f_{x,h}\leq 1$,
$\mathbb {E} f_{x,h}\leq 1$, ![]() $|\mathbb {E} f_{x,h}-\sigma ^2|<\tau ^8/64$, and
$|\mathbb {E} f_{x,h}-\sigma ^2|<\tau ^8/64$, and ![]() $\|\nu _{x,h}-1\|_{U^2(\Phi _{x,h})}<\varepsilon ^{1/32}/\beta \gamma ^2\delta ^2\rho ^{3/2}<\exp (-(64/\tau )^{c_3})$, provided that
$\|\nu _{x,h}-1\|_{U^2(\Phi _{x,h})}<\varepsilon ^{1/32}/\beta \gamma ^2\delta ^2\rho ^{3/2}<\exp (-(64/\tau )^{c_3})$, provided that ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough. Applying Lemma 6.1 on the affine subspace
$c_2$ is large enough. Applying Lemma 6.1 on the affine subspace ![]() $\Phi _{x,h}$ yields a function
$\Phi _{x,h}$ yields a function ![]() $\tilde {f}_{x,h}:\Phi _{x,h}\to [0,1]$ such that
$\tilde {f}_{x,h}:\Phi _{x,h}\to [0,1]$ such that
provided that ![]() $c_3$ is large enough. We must then also have
$c_3$ is large enough. We must then also have
Arguing as in the proof of the first part of Lemma 6.5, it follows that, for every pair ![]() $(x,h)\in A_0$, there exists a nonzero
$(x,h)\in A_0$, there exists a nonzero ![]() $\xi _{x,h}\in \widehat {\Phi _{x,h}-u}$ such that
$\xi _{x,h}\in \widehat {\Phi _{x,h}-u}$ such that
so that
as well.
Extend ![]() $(x,h)\mapsto \xi _{x,h}$ from
$(x,h)\mapsto \xi _{x,h}$ from ![]() $A_0$ to the set
$A_0$ to the set ![]() $\{(x,h)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:x,x+h\in A\}$ by picking a nonzero
$\{(x,h)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:x,x+h\in A\}$ by picking a nonzero ![]() $\xi _{x,h}\in \widehat {\Phi _{x,h}-u}$ arbitrarily for all pairs outside of
$\xi _{x,h}\in \widehat {\Phi _{x,h}-u}$ arbitrarily for all pairs outside of ![]() $A_0$. We split the average over
$A_0$. We split the average over ![]() $y\in \Phi _{x,h}$ up into an average of averages over cosets of
$y\in \Phi _{x,h}$ up into an average of averages over cosets of ![]() $\langle \xi _{x,h}\rangle ^\perp$ and average over all pairs
$\langle \xi _{x,h}\rangle ^\perp$ and average over all pairs ![]() $(x,h)$ such that
$(x,h)$ such that ![]() $x,x+h\in A$ to get that
$x,x+h\in A$ to get that
for some absolute constant ![]() $c>0$. Note that
$c>0$. Note that
 \begin{align*} \mathbb{E}_{x,x+h\in A}\mathbb{E}_{t\in\mathbb{F}_p}\mathbb{E}_{\substack{y\in\Phi_{x,h} \\ \xi_{x,h}\cdot y=t}}(f_{x,h}-\sigma^2)(y) &= \frac{1}{\alpha^2\beta\gamma^2\delta^2\rho^2} \mathbb{E}_{x,y,h}S(x,y)S(x+h,y)-\sigma^2 \\ &= \frac{1}{\alpha^2\beta\gamma^2\delta^2\rho^2}\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y), \end{align*}
\begin{align*} \mathbb{E}_{x,x+h\in A}\mathbb{E}_{t\in\mathbb{F}_p}\mathbb{E}_{\substack{y\in\Phi_{x,h} \\ \xi_{x,h}\cdot y=t}}(f_{x,h}-\sigma^2)(y) &= \frac{1}{\alpha^2\beta\gamma^2\delta^2\rho^2} \mathbb{E}_{x,y,h}S(x,y)S(x+h,y)-\sigma^2 \\ &= \frac{1}{\alpha^2\beta\gamma^2\delta^2\rho^2}\mathbb{E}_{x,y,h}g_S(x,y)g_S(x+h,y), \end{align*}
so that, if it were the case that
then we would be able to deduce the desired density increment from Lemma 6.3. Thus, we may proceed under the assumption
which we can combine with (49), a change of variables, and an application of the pigeonhole principle in the ![]() $t$ variable to deduce that
$t$ variable to deduce that
for some fixed ![]() $t\in \mathbb {F}_p$. Set
$t\in \mathbb {F}_p$. Set
To deduce the desired density increment by applying the pigeonhole principle to (50), we will have to show that almost every set of the form
has close to the ‘correct’ density. Most of the remainder of our argument for ![]() $\|\cdot \|_{\star _1}$ is devoted to this task.
$\|\cdot \|_{\star _1}$ is devoted to this task.
Set ![]() $Q_{x,h}(y):=S(h,y)C(x+y)D(2x+y)$. We start by showing that either
$Q_{x,h}(y):=S(h,y)C(x+y)D(2x+y)$. We start by showing that either ![]() $\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}$ is small for almost every pair
$\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}$ is small for almost every pair ![]() $(x,h)\in A\times A$, or else we can deduce a density increment from Lemmas 6.3 and 6.5. Note first that
$(x,h)\in A\times A$, or else we can deduce a density increment from Lemmas 6.3 and 6.5. Note first that
where ![]() $\mu (y):=\mathbb {E}_{x}A(x)C(x+y)D(2x+y)\Phi (x,y)$. By Lemmas 3.5, 3.6, and 4.1, we have
$\mu (y):=\mathbb {E}_{x}A(x)C(x+y)D(2x+y)\Phi (x,y)$. By Lemmas 3.5, 3.6, and 4.1, we have
so that ![]() $|\mathbb {E}_{x,h,y}A(x)A(h)\Phi _{x,h-x}(y)Q_{x,h}(y)-\sigma \alpha ^2\beta \gamma ^2\delta ^2\rho ^2|<\varepsilon ^{\Omega (1)}/\rho ^{O(1)}$. Similarly, the average
$|\mathbb {E}_{x,h,y}A(x)A(h)\Phi _{x,h-x}(y)Q_{x,h}(y)-\sigma \alpha ^2\beta \gamma ^2\delta ^2\rho ^2|<\varepsilon ^{\Omega (1)}/\rho ^{O(1)}$. Similarly, the average ![]() $\mathbb {E}_{x,h}A(x)A(h)|\mathbb {E}_yQ_{x,h}(y)\Phi _{x,h-x}(y)-\sigma \beta \gamma ^2\delta ^2\rho ^2|^2$ equals
$\mathbb {E}_{x,h}A(x)A(h)|\mathbb {E}_yQ_{x,h}(y)\Phi _{x,h-x}(y)-\sigma \beta \gamma ^2\delta ^2\rho ^2|^2$ equals
and ![]() $\mathbb {E}_{x,y,h,k}A(x)A(h)\Phi _{x,h-x}(y)\Phi _{x,h-x}(y+k)Q_{x,h}(y)Q_{x,h}(y+k)$ equals
$\mathbb {E}_{x,y,h,k}A(x)A(h)\Phi _{x,h-x}(y)\Phi _{x,h-x}(y+k)Q_{x,h}(y)Q_{x,h}(y+k)$ equals
where
By Lemmas 3.5, 3.6, and 4.1, we have
so that
equals
Thus, if
for some ![]() $c'>0$ (to be chosen later), and
$c'>0$ (to be chosen later), and ![]() $c_1$ is small enough and
$c_1$ is small enough and ![]() $c_2$ is large enough, then
$c_2$ is large enough, then
in which case the desired density increment follows from Lemma 6.3. We may thus proceed under the assumption that
so that, by Markov's inequality, we have
It follows that ![]() $\mathbb {E}_{x,h}A(x)A(h)\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}^4$ equals
$\mathbb {E}_{x,h}A(x)A(h)\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}^4$ equals
 \[ \mathbb{E}_{\substack{x,h\in\mathbb{F}_p^n \\ y,y+k,y+\ell\in\Phi_{x,h-x}}}A(x)A(h) \Delta_{k,\ell}Q_{x,h}(y)=\frac{\alpha\gamma^4\delta^4}{\rho^3}\mathbb{E}_{x,y,k,\ell} \Delta_{(0,k),(0,\ell)}S(x,y)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg). \]
\[ \mathbb{E}_{\substack{x,h\in\mathbb{F}_p^n \\ y,y+k,y+\ell\in\Phi_{x,h-x}}}A(x)A(h) \Delta_{k,\ell}Q_{x,h}(y)=\frac{\alpha\gamma^4\delta^4}{\rho^3}\mathbb{E}_{x,y,k,\ell} \Delta_{(0,k),(0,\ell)}S(x,y)+O\bigg(\frac{\varepsilon^{\Omega(1)}}{\rho^{O(1)}}\bigg). \]
If
then we could deduce the desired density increment from Lemma 6.5. Thus, we may proceed under the assumption that this inequality does not hold, which implies that ![]() $\mathbb {E}_{x,h}A(x)A(h)\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}^4 \ll \tau ^{4c'}\alpha ^2\beta ^4\gamma ^8\delta ^8$. It then follows from Markov's inequality that
$\mathbb {E}_{x,h}A(x)A(h)\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}^4 \ll \tau ^{4c'}\alpha ^2\beta ^4\gamma ^8\delta ^8$. It then follows from Markov's inequality that
Next, we will show that, for typical ![]() $(x,h)\in A\times A$, the average size of
$(x,h)\in A\times A$, the average size of ![]() $S(x,y)S(h,y)\Psi _{h}(x,y)$ is not very large. Certainly,
$S(x,y)S(h,y)\Psi _{h}(x,y)$ is not very large. Certainly,
for every ![]() $(x,h)\in A\times A$. Setting
$(x,h)\in A\times A$. Setting
Lemma 3.6 says that
Thus, by Lemma 3.5, as long as ![]() $c_2$ is large enough, we have
$c_2$ is large enough, we have
say.
Now, setting ![]() $c'=8c$, the contribution to the left-hand side of (50) coming from pairs
$c'=8c$, the contribution to the left-hand side of (50) coming from pairs ![]() $(x,h)\in A\times A$ for which
$(x,h)\in A\times A$ for which ![]() $\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}\gg \tau ^{16c}\beta \gamma ^2\delta ^2$ or
$\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}\gg \tau ^{16c}\beta \gamma ^2\delta ^2$ or ![]() $|\mathbb {E}_y S(x,y)S(h,y)\Psi _h(x,y)|>100\beta \gamma ^2\delta ^2\rho ^2/p$ is
$|\mathbb {E}_y S(x,y)S(h,y)\Psi _h(x,y)|>100\beta \gamma ^2\delta ^2\rho ^2/p$ is ![]() $\ll \tau ^{16c}$. Thus, by the pigeonhole principle, there exists an
$\ll \tau ^{16c}$. Thus, by the pigeonhole principle, there exists an ![]() $h\in A$ and a subset
$h\in A$ and a subset ![]() $A'\subset A$ of density
$A'\subset A$ of density ![]() $\alpha '\gg \tau ^{O(1)}\alpha$ in
$\alpha '\gg \tau ^{O(1)}\alpha$ in ![]() $\mathbb {F}_p^n$ such that
$\mathbb {F}_p^n$ such that
and ![]() $\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}\ll \tau ^{16c}\beta \gamma ^2\delta ^2$ for every
$\|Q_{x,h}-\sigma \beta \gamma ^2\delta ^2\|_{U^2(\Phi _{x,h-x})}\ll \tau ^{16c}\beta \gamma ^2\delta ^2$ for every ![]() $x\in A'$. Recalling the definition of
$x\in A'$. Recalling the definition of ![]() $f_{x,h}$, the above displayed equation says that
$f_{x,h}$, the above displayed equation says that
We now use Lemma 6.6 to find a subset ![]() $A''\subset A'$ of density
$A''\subset A'$ of density ![]() $\alpha ''\gg \alpha '\rho \tau ^{O(1)}$ and a
$\alpha ''\gg \alpha '\rho \tau ^{O(1)}$ and a ![]() $u'\in \mathbb {F}_p^n$ such that
$u'\in \mathbb {F}_p^n$ such that
where
This gives the conclusion of the lemma.
The proofs of the two remaining cases are very similar to those appearing in earlier subsections, so we will be more brief in our arguments. Next, assume that
As in the second part of the proof of Lemma 6.5, we may proceed under the assumption that
and use it to show that either
for almost every pair ![]() $(x',y')$ for which
$(x',y')$ for which ![]() $(-x',x'+y')\in S$, or else the desired density increment follows from Lemma 6.3. By Lemmas 3.5, 3.6, and 4.1 and the Cauchy–Schwarz inequality, either
$(-x',x'+y')\in S$, or else the desired density increment follows from Lemma 6.3. By Lemmas 3.5, 3.6, and 4.1 and the Cauchy–Schwarz inequality, either
 \begin{align*}
&\mathbb{E}_{\substack{x',y' \\ (-x',x'+y')\in S}}\mathbb{E}_{x,y}B(y)D(2x+y) \Phi(x,y)S(x,y'-x)S(-x',x+y+x')\\
&\quad =\sigma^2\alpha\beta^3\gamma \delta^3\rho^3+O(\tau^{16}\alpha\beta^3\gamma\delta^3\rho^3)
\end{align*}
\begin{align*}
&\mathbb{E}_{\substack{x',y' \\ (-x',x'+y')\in S}}\mathbb{E}_{x,y}B(y)D(2x+y) \Phi(x,y)S(x,y'-x)S(-x',x+y+x')\\
&\quad =\sigma^2\alpha\beta^3\gamma \delta^3\rho^3+O(\tau^{16}\alpha\beta^3\gamma\delta^3\rho^3)
\end{align*}
and
 \begin{align*}
&\mathbb{E}_{\substack{x',y' \\ (-x',x'+y')\in S}} |\mathbb{E}_{x,y}B(y)D(2x+y)\Phi(x,y)S(x,y'-x)S(-x',x+y+x')-\sigma^2
\alpha\beta^3\gamma\delta^3\rho^3|^2\\&\quad \ll\tau^{32}\alpha^2\beta^6\gamma^2\delta^6\rho^6 \end{align*}
\begin{align*}
&\mathbb{E}_{\substack{x',y' \\ (-x',x'+y')\in S}} |\mathbb{E}_{x,y}B(y)D(2x+y)\Phi(x,y)S(x,y'-x)S(-x',x+y+x')-\sigma^2
\alpha\beta^3\gamma\delta^3\rho^3|^2\\&\quad \ll\tau^{32}\alpha^2\beta^6\gamma^2\delta^6\rho^6 \end{align*}
or else we have the desired density increment from Lemma 6.3. It then follows from Markov's inequality that
for all but a ![]() $\tau /4$-proportion of pairs
$\tau /4$-proportion of pairs ![]() $(x',y')$ for which
$(x',y')$ for which ![]() $(-x',x'+y')\in S$, which means that we can find such a pair for which we also have
$(-x',x'+y')\in S$, which means that we can find such a pair for which we also have
so that we get the desired density increment by taking ![]() $A'=S(x,y'-x)$,
$A'=S(x,y'-x)$, ![]() $B'=B$,
$B'=B$, ![]() $C'=S(-x',x+y+x')$,
$C'=S(-x',x+y+x')$, ![]() $D'=D$, and
$D'=D$, and ![]() $\Phi '=\Phi$ in the definition of
$\Phi '=\Phi$ in the definition of ![]() $T'$.
$T'$.
Now assume that
which means
By Lemma 6.2 and the pigeonhole principle, there exists a subset ![]() $D_0\subset D$ of density at least
$D_0\subset D$ of density at least ![]() $\tau ^2/2$ for which
$\tau ^2/2$ for which
whenever ![]() $z\in D_0$. As in the proof of Lemma 6.3, there is a subset
$z\in D_0$. As in the proof of Lemma 6.3, there is a subset ![]() $D_1\subset D_0$ of density at least
$D_1\subset D_0$ of density at least ![]() $1/2$ in
$1/2$ in ![]() $D_0$ such that either
$D_0$ such that either ![]() $\mathbb {E}_{2x+y=z}g_S(x,y)\geq \tau \alpha \beta \gamma \rho /4$ or
$\mathbb {E}_{2x+y=z}g_S(x,y)\geq \tau \alpha \beta \gamma \rho /4$ or ![]() $\mathbb {E}_{2x+y=z}g_S(x,y)\leq -\tau \alpha \beta \gamma \rho /4$ for all
$\mathbb {E}_{2x+y=z}g_S(x,y)\leq -\tau \alpha \beta \gamma \rho /4$ for all ![]() $z\in D_1$. As in the proof of Lemma 6.3, we can simply take
$z\in D_1$. As in the proof of Lemma 6.3, we can simply take ![]() $D'=D_1$ and
$D'=D_1$ and ![]() $D'=D\setminus D_1$ in these cases, respectively, since, by Lemma 6.2, the fibers
$D'=D\setminus D_1$ in these cases, respectively, since, by Lemma 6.2, the fibers ![]() $\{(x,y)\in T:2x+y=z\}$ typically have very close to their average size.
$\{(x,y)\in T:2x+y=z\}$ typically have very close to their average size.
7. Pseudorandomization
This section begins with yet more preliminaries. To prove Lemma 2.6, we will need a result of Cohen and Tal, which says that, for any finite set of polynomials in ![]() $\mathbb {F}_p[x_1,\ldots,x_m]$, one can find a partition of
$\mathbb {F}_p[x_1,\ldots,x_m]$, one can find a partition of ![]() $\mathbb {F}_p^m$ into affine subspaces of relatively large dimension on which all of the polynomials are constant.
$\mathbb {F}_p^m$ into affine subspaces of relatively large dimension on which all of the polynomials are constant.
Theorem 7.1 (Cohen and Tal [Theorem 3.6, Reference Cohen and TalCT15] specialized to prime fields)
Let ![]() $d,m,$ and
$d,m,$ and ![]() $t$ be natural numbers. There exists a positive integer
$t$ be natural numbers. There exists a positive integer ![]() $m'$ satisfying
$m'$ satisfying
such that, for any polynomials ![]() $P_1,\ldots,P_t\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most
$P_1,\ldots,P_t\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most ![]() $d$, there is a partition of
$d$, there is a partition of ![]() $\mathbb {F}_p^m$ into affine subspaces of dimension
$\mathbb {F}_p^m$ into affine subspaces of dimension ![]() $m'$ such that
$m'$ such that ![]() $P_1,\ldots,P_t$ are constant on each affine subspace.
$P_1,\ldots,P_t$ are constant on each affine subspace.
To see that this formulation of Cohen and Tal's theorem is equivalent to Theorem 3.6 of [Reference Cohen and TalCT15], note that one can make all of the affine subspaces in the partitions produced by their theorem have the same dimension by simply partitioning each subspace not of the minimum possible dimension into more subspaces.
We will also need a ‘bilinear’ version of Cohen and Tal's result, which we will use to find partitions of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ into product spaces of the form
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ into product spaces of the form ![]() $(u+V)\times (w+V)$ on which polynomials in two sets of variables
$(u+V)\times (w+V)$ on which polynomials in two sets of variables ![]() $x_1,\ldots,x_m,y_1,\ldots,y_m$ are constant.
$x_1,\ldots,x_m,y_1,\ldots,y_m$ are constant.
Corollary 7.2 Let ![]() $d$ and
$d$ and ![]() $m$ be natural numbers. There exists a positive integer
$m$ be natural numbers. There exists a positive integer ![]() $m'$ satisfying
$m'$ satisfying
such that, for any polynomial ![]() $R\in \mathbb {F}_p[x_1,\ldots,x_m,y_1,\ldots,y_m]$ of degree at most
$R\in \mathbb {F}_p[x_1,\ldots,x_m,y_1,\ldots,y_m]$ of degree at most ![]() $d$, there is a partition of
$d$, there is a partition of ![]() $\mathbb {F}_p^m\times \mathbb {F}_p^m$ into products of affine subspaces of the form
$\mathbb {F}_p^m\times \mathbb {F}_p^m$ into products of affine subspaces of the form
with each ![]() $\dim V= m'$, such that
$\dim V= m'$, such that ![]() $R$ is constant on each product of affine subspaces.
$R$ is constant on each product of affine subspaces.
Proof. Write
 \[ R(\mathbf{x},\mathbf{y})=\sum_{i=0}^dP_i(\mathbf{x})Q_i(\mathbf{y}), \]
\[ R(\mathbf{x},\mathbf{y})=\sum_{i=0}^dP_i(\mathbf{x})Q_i(\mathbf{y}), \]
where ![]() $P_0,\ldots,P_d,Q_0,\ldots,Q_d\in \mathbb {F}_p[z_1,\ldots,z_m]$ satisfy
$P_0,\ldots,P_d,Q_0,\ldots,Q_d\in \mathbb {F}_p[z_1,\ldots,z_m]$ satisfy ![]() $\deg {P_i}\leq i$ and
$\deg {P_i}\leq i$ and ![]() $\deg {Q_i}\leq d-i$ for all
$\deg {Q_i}\leq d-i$ for all ![]() $0\leq i \leq d$. Applying Theorem 7.1 to
$0\leq i \leq d$. Applying Theorem 7.1 to ![]() $P_0,\ldots,P_d$ gives us a positive integer
$P_0,\ldots,P_d$ gives us a positive integer ![]() $m'_0\gg {m^{1/(d-1)!}}/{(d+1)^e}$ and a partition
$m'_0\gg {m^{1/(d-1)!}}/{(d+1)^e}$ and a partition
of ![]() $\mathbb {F}_p^m$, with
$\mathbb {F}_p^m$, with ![]() $\dim {V_j}=m'_0$ for each
$\dim {V_j}=m'_0$ for each ![]() $j\in J$, such that
$j\in J$, such that ![]() $P_0,\ldots,P_d$ are all constant on each affine subspace
$P_0,\ldots,P_d$ are all constant on each affine subspace ![]() $u_j+V_j$.
$u_j+V_j$.
Now write
Since restricting a polynomial to a subspace cannot increase its degree, for each ![]() $j\in J$, we can apply Theorem 7.1 on each affine subspace
$j\in J$, we can apply Theorem 7.1 on each affine subspace ![]() $w+V_j$ to the polynomial
$w+V_j$ to the polynomial
 \[ Q_{j,w}(\mathbf{y}):=\sum_{i=0}^dP_i(u_j+V_j)Q_i(\mathbf{y}) \]
\[ Q_{j,w}(\mathbf{y}):=\sum_{i=0}^dP_i(u_j+V_j)Q_i(\mathbf{y}) \]
to get that there exists a positive integer ![]() $m'$ satisfying
$m'$ satisfying
and a partition
with each subspace ![]() $V_k'\leq V_j$ having
$V_k'\leq V_j$ having ![]() $\dim V_k'=m'$, such that
$\dim V_k'=m'$, such that ![]() $Q_{j,w}$ is constant on each
$Q_{j,w}$ is constant on each ![]() $w_k+V_k'$.
$w_k+V_k'$.
Thus, we can write
where ![]() $R$ is constant on each product
$R$ is constant on each product ![]() $(u_j+V_j)\times (w_k+V_k')$. Since
$(u_j+V_j)\times (w_k+V_k')$. Since ![]() $V_k'\leq V_j$ we can further refine this partition to one of the desired form
$V_k'\leq V_j$ we can further refine this partition to one of the desired form
on each part of which ![]() $R$ is still constant.
$R$ is still constant.
Finally, we will recall the recent quantitative inverse theorem of Gowers and Milićević for the ![]() $U^s$-norms on vector spaces over finite fields.
$U^s$-norms on vector spaces over finite fields.
Theorem 7.3 (Gowers and Milićević [Theorem 7, Reference Gowers and MilićevićGM20])
Let ![]() $s$ be a natural number and assume that
$s$ be a natural number and assume that ![]() $p\geq s$. There exist constants
$p\geq s$. There exist constants ![]() $c_s,c_{s,p}'>0$ so that, if
$c_s,c_{s,p}'>0$ so that, if ![]() $f:\mathbb {F}_p^m\to \mathbb {C}$ is a
$f:\mathbb {F}_p^m\to \mathbb {C}$ is a ![]() $1$-bounded function satisfying
$1$-bounded function satisfying
then there exists a polynomial ![]() $P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree
$P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree ![]() $\deg {P}\leq s-1$ such that
$\deg {P}\leq s-1$ such that
7.1 Proof of Lemma 2.6
Our proof of Lemma 2.6 is modeled after the corresponding pseudorandomization arguments in [Reference ShkredovShk06a, Reference ShkredovShk06b] and [Reference GreenGre05a]. As was said in the outline, some new features arise from our desire for ![]() $B',C',D',$ and
$B',C',D',$ and ![]() $\Phi '$ to be uniform with respect to
$\Phi '$ to be uniform with respect to ![]() $U^s$-norms of degree greater than
$U^s$-norms of degree greater than ![]() $2$ and from
$2$ and from ![]() $\Phi$'s particular structure as a union of affine subspaces of the second factor of
$\Phi$'s particular structure as a union of affine subspaces of the second factor of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$. The first of these two complications can be overcome by using Theorem 7.3 and then Theorem 7.1 or Corollary 7.2. We will discuss how
$\mathbb {F}_p^n\times \mathbb {F}_p^n$. The first of these two complications can be overcome by using Theorem 7.3 and then Theorem 7.1 or Corollary 7.2. We will discuss how ![]() $\Phi$'s structure influences our proof shortly.
$\Phi$'s structure influences our proof shortly.
The proof of Lemma 2.6 proceeds via an energy-increment argument. Each step of the energy-increment iteration will produce a partition ![]() $\mathscr {C}_{j}=(\mathcal {C}_{i,j})_{i\in I_j}$ of
$\mathscr {C}_{j}=(\mathcal {C}_{i,j})_{i\in I_j}$ of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ into cells
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ into cells ![]() $\mathcal {C}_{i,j}$ of the form
$\mathcal {C}_{i,j}$ of the form
for some subspace ![]() $V_{i,j}\leq \mathbb {F}_p^n$. For each cell
$V_{i,j}\leq \mathbb {F}_p^n$. For each cell ![]() $\mathcal {C}=(u+V)\times (w+V)$ in a partition
$\mathcal {C}=(u+V)\times (w+V)$ in a partition ![]() $\mathscr {C}$, we set
$\mathscr {C}$, we set
–
 $B_{\mathcal {C}}:= B\cap (w+V)$,
$B_{\mathcal {C}}:= B\cap (w+V)$,–
 $C_{\mathcal {C}}:= C\cap (u+w+V)$,
$C_{\mathcal {C}}:= C\cap (u+w+V)$,–
 $D_{\mathcal {C}}:= D\cap (2u+w+V)$, and
$D_{\mathcal {C}}:= D\cap (2u+w+V)$, and–
 $\Phi _{\mathcal {C}}:=\Phi \cap \mathcal {C}$,
$\Phi _{\mathcal {C}}:=\Phi \cap \mathcal {C}$,
and, correspondingly,
–
 $\beta (\mathcal {C}):=\mu _{w+V}(B_{\mathcal {C}})$,
$\beta (\mathcal {C}):=\mu _{w+V}(B_{\mathcal {C}})$,–
 $\gamma (\mathcal {C}):=\mu _{u+w+V}(C_{\mathcal {C}})$,
$\gamma (\mathcal {C}):=\mu _{u+w+V}(C_{\mathcal {C}})$,–
 $\delta (\mathcal {C}):=\mu _{2u+w+V}(D_{\mathcal {C}})$, and
$\delta (\mathcal {C}):=\mu _{2u+w+V}(D_{\mathcal {C}})$, and–
 $\phi (\mathcal {C}):=\mu _{\mathcal {C}}(\Phi _{\mathcal {C}})$,
$\phi (\mathcal {C}):=\mu _{\mathcal {C}}(\Phi _{\mathcal {C}})$,
so that
Analogously to the pseudorandomization procedure for corners, we will show that if ![]() $\|B_{\mathcal {C}}-\beta (\mathcal {C})\|_{U^8(\mathbb {F}_p^n)},\|C_{\mathcal {C}}-\gamma (\mathcal {C})\|_{U^8(\mathbb {F}_p^n)},$ or
$\|B_{\mathcal {C}}-\beta (\mathcal {C})\|_{U^8(\mathbb {F}_p^n)},\|C_{\mathcal {C}}-\gamma (\mathcal {C})\|_{U^8(\mathbb {F}_p^n)},$ or ![]() $\|D_{\mathcal {C}}-\delta (\mathcal {C})\|_{U^8(\mathbb {F}_p^n)}$ is large for a substantial portion of cells
$\|D_{\mathcal {C}}-\delta (\mathcal {C})\|_{U^8(\mathbb {F}_p^n)}$ is large for a substantial portion of cells ![]() $\mathcal {C}$ in a partition
$\mathcal {C}$ in a partition ![]() $\mathscr {C}$, then there exists a refinement
$\mathscr {C}$, then there exists a refinement ![]() $\mathscr {C}'$ of
$\mathscr {C}'$ of ![]() $\mathscr {C}$ which has substantially larger energy. But even if
$\mathscr {C}$ which has substantially larger energy. But even if ![]() $\Phi _{\mathcal {C}}$ is a union of affine subspaces of the same codimension
$\Phi _{\mathcal {C}}$ is a union of affine subspaces of the same codimension ![]() $d$ for most cells in the partition, this may not be the case for the
$d$ for most cells in the partition, this may not be the case for the ![]() $\Phi _{\mathcal {C}'}$ corresponding to the cells
$\Phi _{\mathcal {C}'}$ corresponding to the cells ![]() $\mathcal {C}'$ in the refinement
$\mathcal {C}'$ in the refinement ![]() $\mathscr {C}'$. The codimensions of the affine subspaces
$\mathscr {C}'$. The codimensions of the affine subspaces ![]() $\{y\in w'+V':\Phi _{\mathcal {C}'}(x,y)=1\}$ can range from
$\{y\in w'+V':\Phi _{\mathcal {C}'}(x,y)=1\}$ can range from ![]() $0$ to
$0$ to ![]() $d$, so before even considering how to obtain a pseudorandom
$d$, so before even considering how to obtain a pseudorandom ![]() $\Phi '$, we have already found an obstacle to even getting a set of the same general form as
$\Phi '$, we have already found an obstacle to even getting a set of the same general form as ![]() $\Phi '$.
$\Phi '$.
To get around this issue, we will pseudorandomize each of the sets
for ![]() $0\leq i\leq d$, instead of just
$0\leq i\leq d$, instead of just ![]() $\Phi _{\mathcal {C}}=\Phi ^{\leq d}_{\mathcal {C}}$ itself. The definition (54) of
$\Phi _{\mathcal {C}}=\Phi ^{\leq d}_{\mathcal {C}}$ itself. The definition (54) of ![]() $\Phi ^{\leq i}_{\mathcal {C}}$ selects all of the subspaces of the second factor of
$\Phi ^{\leq i}_{\mathcal {C}}$ selects all of the subspaces of the second factor of ![]() $\mathcal {C}$ comprising
$\mathcal {C}$ comprising ![]() $\Phi _{\mathcal {C}}$ that have codimension at most
$\Phi _{\mathcal {C}}$ that have codimension at most ![]() $i$. This will pseudorandomize each of
$i$. This will pseudorandomize each of
as well. At the end of the proof of Lemma 2.6, we will use an averaging argument to choose ![]() $\Phi '$ to be some suitable
$\Phi '$ to be some suitable ![]() $\Phi _{\mathcal {C}}^i$.
$\Phi _{\mathcal {C}}^i$.
For each ![]() $0\leq i\leq d$, set
$0\leq i\leq d$, set ![]() $\phi ^{\leq i}(\mathcal {C}):=\mu _{\mathcal {C}}(\Phi _{\mathcal {C}}^{\leq i})$. We define the energy
$\phi ^{\leq i}(\mathcal {C}):=\mu _{\mathcal {C}}(\Phi _{\mathcal {C}}^{\leq i})$. We define the energy ![]() $E(\mathscr {C})$ of a partition
$E(\mathscr {C})$ of a partition ![]() $\mathscr {C}$ of
$\mathscr {C}$ of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ by
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ by
 \[ E(\mathscr{C}):=\frac{1}{4+d}\sum_{\mathcal{C}\in\mathscr{C}} \bigg(\beta(\mathcal{C})^2+\gamma(\mathcal{C})^2+\delta(\mathcal{C})^2+ \sum_{i=0}^d\phi^{\leq i}(\mathcal{C})^2\bigg)\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}). \]
\[ E(\mathscr{C}):=\frac{1}{4+d}\sum_{\mathcal{C}\in\mathscr{C}} \bigg(\beta(\mathcal{C})^2+\gamma(\mathcal{C})^2+\delta(\mathcal{C})^2+ \sum_{i=0}^d\phi^{\leq i}(\mathcal{C})^2\bigg)\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}). \]
Note that the energy of any partition is bounded above by ![]() $1$. We will now prove a couple of lemmas concerning this energy.
$1$. We will now prove a couple of lemmas concerning this energy.
Lemma 7.4 Let ![]() $m'>m$ and
$m'>m$ and ![]() $d$ be nonnegative integers,
$d$ be nonnegative integers, ![]() $A,B,C,D\subset \mathbb {F}_p^n$,
$A,B,C,D\subset \mathbb {F}_p^n$, ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be of the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be of the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension between
$\mathbb {F}_p^n$ of codimension between ![]() $0$ and
$0$ and ![]() $d$,
$d$, ![]() $\mathscr {C}$ be a partition of
$\mathscr {C}$ be a partition of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ with each cell
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ with each cell ![]() $\mathcal {C}$ taking the form
$\mathcal {C}$ taking the form
for some subspace ![]() $V_{\mathcal {C}}\leq \mathbb {F}_p^n$ of codimension
$V_{\mathcal {C}}\leq \mathbb {F}_p^n$ of codimension ![]() $m$, and suppose that
$m$, and suppose that ![]() $\mathscr {C}'$ is a refinement of
$\mathscr {C}'$ is a refinement of ![]() $\mathscr {C}$ with each cell
$\mathscr {C}$ with each cell ![]() $\mathcal {C}'$ taking the form
$\mathcal {C}'$ taking the form
for some subspace ![]() $V'_{\mathcal {C}'}$ of codimension
$V'_{\mathcal {C}'}$ of codimension ![]() $m'$. Then
$m'$. Then
 \begin{gather*} \sum_{\mathcal{C}'\in\mathscr{C}'}\beta(\mathcal{C}')^2 \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')\geq\sum_{\mathcal{C}\in\mathscr{C}} \beta(\mathcal{C})^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}),\\ \sum_{\mathcal{C}'\in\mathscr{C}'}\gamma(\mathcal{C}')^2 \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')\geq\sum_{\mathcal{C}\in\mathscr{C}} \gamma(\mathcal{C})^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}),\\ \sum_{\mathcal{C}'\in\mathscr{C}'}\delta(\mathcal{C}')^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n} (\mathcal{C}')\geq\sum_{\mathcal{C}\in\mathscr{C}}\delta(\mathcal{C})^2 \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}), \end{gather*}
\begin{gather*} \sum_{\mathcal{C}'\in\mathscr{C}'}\beta(\mathcal{C}')^2 \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')\geq\sum_{\mathcal{C}\in\mathscr{C}} \beta(\mathcal{C})^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}),\\ \sum_{\mathcal{C}'\in\mathscr{C}'}\gamma(\mathcal{C}')^2 \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')\geq\sum_{\mathcal{C}\in\mathscr{C}} \gamma(\mathcal{C})^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}),\\ \sum_{\mathcal{C}'\in\mathscr{C}'}\delta(\mathcal{C}')^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n} (\mathcal{C}')\geq\sum_{\mathcal{C}\in\mathscr{C}}\delta(\mathcal{C})^2 \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}), \end{gather*}
and
for every ![]() $0\leq i\leq d$.
$0\leq i\leq d$.
Proof. Note that it suffices to prove the result with the sum over ![]() $\mathcal {C}\in \mathscr {C}$ restricted to a single cell
$\mathcal {C}\in \mathscr {C}$ restricted to a single cell ![]() $\mathcal {C}_0$ and the sum over
$\mathcal {C}_0$ and the sum over ![]() $\mathcal {C}'\in \mathscr {C}'$ restricted to all cells contained in
$\mathcal {C}'\in \mathscr {C}'$ restricted to all cells contained in ![]() $\mathcal {C}_0$, since one can then just sum over
$\mathcal {C}_0$, since one can then just sum over ![]() $\mathcal {C}_0$ in
$\mathcal {C}_0$ in ![]() $\mathscr {C}$ to get the desired result. Thus, we may assume without loss of generality that
$\mathscr {C}$ to get the desired result. Thus, we may assume without loss of generality that ![]() $\mathscr {C}$ is the trivial partition
$\mathscr {C}$ is the trivial partition ![]() $\{\mathbb {F}_p^n\times \mathbb {F}_p^n\}$.
$\{\mathbb {F}_p^n\times \mathbb {F}_p^n\}$.
Let ![]() $\beta,\gamma,$ and
$\beta,\gamma,$ and ![]() $\delta$ denote the densities of
$\delta$ denote the densities of ![]() $B,C,$ and
$B,C,$ and ![]() $D$, respectively, in
$D$, respectively, in ![]() $\mathbb {F}_p^n$. Since
$\mathbb {F}_p^n$. Since ![]() $\mathbb {F}_p^n\times B$ has density
$\mathbb {F}_p^n\times B$ has density ![]() $\beta$ in
$\beta$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$, we have
$\mathbb {F}_p^n\times \mathbb {F}_p^n$, we have
so that, by the Cauchy–Schwarz inequality,
 \begin{align*} \beta^2&\leq\bigg(\sum_{\mathcal{C}'\in\mathscr{C}'}\beta(\mathcal{C}')^2\bigg) \bigg(\sum_{\mathcal{C}'\in\mathscr{C}'}\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')^2\bigg) \\ &=\sum_{\mathcal{C}'\in\mathscr{C}'}\beta(\mathcal{C}')^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}'), \end{align*}
\begin{align*} \beta^2&\leq\bigg(\sum_{\mathcal{C}'\in\mathscr{C}'}\beta(\mathcal{C}')^2\bigg) \bigg(\sum_{\mathcal{C}'\in\mathscr{C}'}\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')^2\bigg) \\ &=\sum_{\mathcal{C}'\in\mathscr{C}'}\beta(\mathcal{C}')^2\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}'), \end{align*}
as desired, since
 \[ \sum_{\mathcal{C}'\in\mathscr{C}'}\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')^2= \frac{p^{2n}}{p^{2n-2m'}}\cdot \frac{1}{p^{4m'}}=\frac{1}{p^{2m'}}=\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}') \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}'}\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}')^2= \frac{p^{2n}}{p^{2n-2m'}}\cdot \frac{1}{p^{4m'}}=\frac{1}{p^{2m'}}=\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(\mathcal{C}') \]
for all cells ![]() $\mathcal {C}'$ of
$\mathcal {C}'$ of ![]() $\mathscr {C}'$. Similarly, since
$\mathscr {C}'$. Similarly, since ![]() $\{(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:x+y\in C\}$ has density
$\{(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:x+y\in C\}$ has density ![]() $\gamma$ in
$\gamma$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ and
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ and ![]() $\{(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:2x+y\in D\}$ has density
$\{(x,y)\in \mathbb {F}_p^n\times \mathbb {F}_p^n:2x+y\in D\}$ has density ![]() $\delta$ in
$\delta$ in ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$, we have
$\mathbb {F}_p^n\times \mathbb {F}_p^n$, we have
and
it follows again from the Cauchy–Schwarz inequality that
and
The argument for the ![]() $\phi ^{\leq i}$ is also essentially identical, but with one small difference. For ease of notation, set
$\phi ^{\leq i}$ is also essentially identical, but with one small difference. For ease of notation, set ![]() $\Phi ^{\leq i}:=\Phi ^{\leq i}_{\mathbb {F}_p^n\times \mathbb {F}_p^n}$ and
$\Phi ^{\leq i}:=\Phi ^{\leq i}_{\mathbb {F}_p^n\times \mathbb {F}_p^n}$ and ![]() $\phi ^{\leq i}:=\phi ^{\leq i}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$ for all
$\phi ^{\leq i}:=\phi ^{\leq i}(\mathbb {F}_p^n\times \mathbb {F}_p^n)$ for all ![]() $0\leq i\leq d$. Then we actually have
$0\leq i\leq d$. Then we actually have
instead of equality, since ![]() $\Phi ^{\leq i}\cap \mathcal {C}'\subset \Phi ^{\leq i}_{\mathcal {C}'}$ (which is why we run the energy-increment argument with the
$\Phi ^{\leq i}\cap \mathcal {C}'\subset \Phi ^{\leq i}_{\mathcal {C}'}$ (which is why we run the energy-increment argument with the ![]() $\Phi ^{\leq i}$, instead of the
$\Phi ^{\leq i}$, instead of the ![]() $\Phi ^i$). It therefore follows yet again from the Cauchy–Schwarz inequality that
$\Phi ^i$). It therefore follows yet again from the Cauchy–Schwarz inequality that
for all ![]() $0\leq i\leq d$.
$0\leq i\leq d$.
Lemma 7.5 Let ![]() $m$ and
$m$ and ![]() $d$ be nonnegative integers,
$d$ be nonnegative integers, ![]() $A,B,C,D\subset \mathbb {F}_p^n$,
$A,B,C,D\subset \mathbb {F}_p^n$, ![]() $\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be of the form
$\Phi \subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ be of the form
where each ![]() $V_x$ is a subspace of
$V_x$ is a subspace of ![]() $\mathbb {F}_p^n$ of codimension between
$\mathbb {F}_p^n$ of codimension between ![]() $0$ and
$0$ and ![]() $d$, and
$d$, and ![]() $\mathscr {C}$ be a partition of
$\mathscr {C}$ be a partition of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$ with each cell
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ with each cell ![]() $\mathcal {C}$ taking the form
$\mathcal {C}$ taking the form
for some subspace ![]() $V_{\mathcal {C}}\leq \mathbb {F}_p^n$ of dimension
$V_{\mathcal {C}}\leq \mathbb {F}_p^n$ of dimension ![]() $m$. There exists a positive integer
$m$. There exists a positive integer
and positive integers ![]() $c,c'_p>0$, such that the following holds.
$c,c'_p>0$, such that the following holds.
Let ![]() $\mathcal {C}\in \mathscr {C}$.
$\mathcal {C}\in \mathscr {C}$.
(i) If
 $\|B_{\mathcal {C}}-\beta (\mathcal {C})\|_{U^{10}(w_\mathcal {C}+V_{\mathcal {C}})}\geq \varepsilon$, then there exists a partition
$\|B_{\mathcal {C}}-\beta (\mathcal {C})\|_{U^{10}(w_\mathcal {C}+V_{\mathcal {C}})}\geq \varepsilon$, then there exists a partition  $\mathscr {C}'_{\mathcal {C}}$ of
$\mathscr {C}'_{\mathcal {C}}$ of  $\mathcal {C}$ with each cell
$\mathcal {C}$ with each cell  $\mathcal {C}'$ taking the form
with each
$\mathcal {C}'$ taking the form
with each \[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
\[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
 $\dim V_{C'}'=m'$, such that
$\dim V_{C'}'=m'$, such that
 \[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\beta(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\beta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\beta(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\beta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
(ii) If
 $\|C_{\mathcal {C}}-\gamma (\mathcal {C})\|_{U^{10}(u_{\mathcal {C}}+w_\mathcal {C}+V_{\mathcal {C}})}\geq \varepsilon$, then there exists a partition
$\|C_{\mathcal {C}}-\gamma (\mathcal {C})\|_{U^{10}(u_{\mathcal {C}}+w_\mathcal {C}+V_{\mathcal {C}})}\geq \varepsilon$, then there exists a partition  $\mathscr {C}'_{\mathcal {C}}$ of
$\mathscr {C}'_{\mathcal {C}}$ of  $\mathcal {C}$ with each cell
$\mathcal {C}$ with each cell  $\mathcal {C}'$ taking the form
with each
$\mathcal {C}'$ taking the form
with each \[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
\[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
 $\dim V_{C'}'=m'$, such that
$\dim V_{C'}'=m'$, such that
 \[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\gamma(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\gamma(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\gamma(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\gamma(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
(iii) If
 $\|D_{\mathcal {C}}-\delta (\mathcal {C})\|_{U^{10}(2u_{\mathcal {C}}+w_\mathcal {C}+V_{\mathcal {C}})}\geq \varepsilon$, then there exists a partition
$\|D_{\mathcal {C}}-\delta (\mathcal {C})\|_{U^{10}(2u_{\mathcal {C}}+w_\mathcal {C}+V_{\mathcal {C}})}\geq \varepsilon$, then there exists a partition  $\mathscr {C}'_{\mathcal {C}}$ of
$\mathscr {C}'_{\mathcal {C}}$ of  $\mathcal {C}$ with each cell
$\mathcal {C}$ with each cell  $\mathcal {C}'$ taking the form
with each
$\mathcal {C}'$ taking the form
with each \[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
\[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
 $\dim V_{C'}'=m'$, such that
$\dim V_{C'}'=m'$, such that
 \[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\delta(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\delta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\delta(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\delta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
(iv) Let
 $0\leq i\leq d$. If
$0\leq i\leq d$. If  $\|\Phi ^{\leq i}_{\mathcal {C}}-\phi ^{\leq i} (\mathcal {C})\|_{U^{8}(\mathcal {C})}\geq \varepsilon$, then there exists a partition
$\|\Phi ^{\leq i}_{\mathcal {C}}-\phi ^{\leq i} (\mathcal {C})\|_{U^{8}(\mathcal {C})}\geq \varepsilon$, then there exists a partition  $\mathscr {C}'_{\mathcal {C}}$ of
$\mathscr {C}'_{\mathcal {C}}$ of  $\mathcal {C}$ with each cell
$\mathcal {C}$ with each cell  $\mathcal {C}'$ taking the form
with each
$\mathcal {C}'$ taking the form
with each \[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
\[ \mathcal{C}'=(u_{\mathcal{C}'}'+V_{\mathcal{C}'}')\times(w_{\mathcal{C}'}'+V_{\mathcal{C}'}'), \]
 $\dim V_{C'}'=m'$, such that
$\dim V_{C'}'=m'$, such that
 \[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\phi^{\leq i}(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\phi^{\leq i}(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\phi^{\leq i}(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\phi^{\leq i}(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg). \]
Proof. Let ![]() $c$ and
$c$ and ![]() $c'_p$ denote the constants
$c'_p$ denote the constants ![]() $c_{10}$ and
$c_{10}$ and ![]() $c_{10,p}'$, respectively, from Theorem 7.3, and
$c_{10,p}'$, respectively, from Theorem 7.3, and ![]() $m'$ denote the smaller of the two minimum values of
$m'$ denote the smaller of the two minimum values of ![]() $m'$ appearing in Theorem 7.1 when we take
$m'$ appearing in Theorem 7.1 when we take ![]() $m$ as in this lemma,
$m$ as in this lemma, ![]() $d=9$, and
$d=9$, and ![]() $t=1$ and
$t=1$ and ![]() $m'$ appearing in Corollary 7.2 when we take
$m'$ appearing in Corollary 7.2 when we take ![]() $m$ as in this lemma and
$m$ as in this lemma and ![]() $d=7$.
$d=7$.
First assume that ![]() $\|B_{\mathcal {C}}-\beta (\mathcal {C})\|_{U^{10}(w_{\mathcal {C}}+V_{\mathcal {C}})}\geq \varepsilon$. Then applying Theorem 7.3 with
$\|B_{\mathcal {C}}-\beta (\mathcal {C})\|_{U^{10}(w_{\mathcal {C}}+V_{\mathcal {C}})}\geq \varepsilon$. Then applying Theorem 7.3 with ![]() $s=10$ yields a polynomial
$s=10$ yields a polynomial ![]() $P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most
$P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most ![]() $9$ such that
$9$ such that
By Theorem 7.1, there exists a partition ![]() $(w_i+V_i)_{i\in I}$ of
$(w_i+V_i)_{i\in I}$ of ![]() $w_{\mathcal {C}}+V_{\mathcal {C}}$ into affine subspaces of
$w_{\mathcal {C}}+V_{\mathcal {C}}$ into affine subspaces of ![]() $w_{\mathcal {C}}+V_{\mathcal {C}}$ of dimension
$w_{\mathcal {C}}+V_{\mathcal {C}}$ of dimension ![]() $m'$, on each of which
$m'$, on each of which ![]() $P$ is constant. Thus, by the triangle inequality,
$P$ is constant. Thus, by the triangle inequality,
so that, by the Cauchy–Schwarz inequality,
Expanding the square, this means that
Now we partition the whole cell of interest ![]() $\mathcal {C}$ by writing
$\mathcal {C}$ by writing
and, for each ![]() $i\in I$, use that
$i\in I$, use that ![]() $V_i\leq V_{\mathcal {C}}$ to partition
$V_i\leq V_{\mathcal {C}}$ to partition ![]() $u_{\mathcal {C}}+V_{\mathcal {C}}$ into cosets of
$u_{\mathcal {C}}+V_{\mathcal {C}}$ into cosets of ![]() $V_i$ to get
$V_i$ to get
Since ![]() $\mu _{\mathcal {C}}(\mathcal {C}')=|\mathscr {C}'|^{-1}$ for each
$\mu _{\mathcal {C}}(\mathcal {C}')=|\mathscr {C}'|^{-1}$ for each ![]() $\mathcal {C}'\in \mathscr {C}_{\mathcal {C}}'$, (55) reads
$\mathcal {C}'\in \mathscr {C}_{\mathcal {C}}'$, (55) reads
 \[ \sum_{\mathcal{C}'\in\mathscr{C}_{\mathcal{C}}'}\beta(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\beta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^{c}(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}_{\mathcal{C}}'}\beta(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\beta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^{c}(c'_p/\varepsilon)^2}\bigg). \]
The arguments for ![]() $C_{\mathcal {C}}$ and
$C_{\mathcal {C}}$ and ![]() $D_{\mathcal {C}}$ are again analogous, but we include them for the sake of completeness. Next, assume that
$D_{\mathcal {C}}$ are again analogous, but we include them for the sake of completeness. Next, assume that ![]() $\|C_{\mathcal {C}}-\gamma (\mathcal {C})\|_{U^{10}(u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}})}\geq \varepsilon$. Applying Theorem 7.3 yields a polynomial
$\|C_{\mathcal {C}}-\gamma (\mathcal {C})\|_{U^{10}(u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}})}\geq \varepsilon$. Applying Theorem 7.3 yields a polynomial ![]() $P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most
$P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most ![]() $9$ such that
$9$ such that
By Theorem 7.1, there exists a partition ![]() $(v_i+V_i)_{i\in I}$ of
$(v_i+V_i)_{i\in I}$ of ![]() $u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ into affine subspaces of
$u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ into affine subspaces of ![]() $u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ of dimension
$u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ of dimension ![]() $m'$ on each of which
$m'$ on each of which ![]() $P$ is constant. Thus, by the Cauchy–Schwarz inequality again,
$P$ is constant. Thus, by the Cauchy–Schwarz inequality again,
Now we partition the whole cell ![]() $\mathcal {C}$ by writing
$\mathcal {C}$ by writing
Since ![]() $(v_i-w_{\mathcal {C}}+v'+V_i)+(w_{\mathcal {C}}-v'+V_i)=v_i+V_i$, we conclude that
$(v_i-w_{\mathcal {C}}+v'+V_i)+(w_{\mathcal {C}}-v'+V_i)=v_i+V_i$, we conclude that
 \[ \sum_{\mathcal{C}'\in\mathscr{C}_{\mathcal{C}}'}\gamma(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\gamma(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^{c}(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}_{\mathcal{C}}'}\gamma(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\gamma(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^{c}(c'_p/\varepsilon)^2}\bigg). \]
Now assume that ![]() $\|D_{\mathcal {C}}-\delta (\mathcal {C})\|_{U^{10}(2u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}})}\geq \varepsilon$. Applying Theorem 7.3 yields a polynomial
$\|D_{\mathcal {C}}-\delta (\mathcal {C})\|_{U^{10}(2u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}})}\geq \varepsilon$. Applying Theorem 7.3 yields a polynomial ![]() $P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most
$P\in \mathbb {F}_p[x_1,\ldots,x_m]$ of degree at most ![]() $9$ such that
$9$ such that
By Theorem 7.1, there exists a partition ![]() $(v_i+V_i)_{i\in I}$ of
$(v_i+V_i)_{i\in I}$ of ![]() $2u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ into affine subspaces of
$2u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ into affine subspaces of ![]() $2u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ of dimension
$2u_{\mathcal {C}}+w_{\mathcal {C}}+V_{\mathcal {C}}$ of dimension ![]() $m'$ on each of which
$m'$ on each of which ![]() $P$ is constant. Thus, by the Cauchy–Schwarz inequality yet again,
$P$ is constant. Thus, by the Cauchy–Schwarz inequality yet again,
Now we partition the whole cell ![]() $\mathcal {C}$ by writing
$\mathcal {C}$ by writing
Since ![]() $(2u_{\mathcal {C}}+2v'+V_i)+(v_i-2u_{\mathcal {C}}-2v'+V_i)=v_i+V_i$, we conclude that
$(2u_{\mathcal {C}}+2v'+V_i)+(v_i-2u_{\mathcal {C}}-2v'+V_i)=v_i+V_i$, we conclude that
 \[ \sum_{\mathcal{C}'\in\mathscr{C}_{\mathcal{C}}'}\delta(\mathcal{C}')^2\mu_{\mathcal{C}} (\mathcal{C}')\geq\delta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^{c}(c'_p/\varepsilon)^2}\bigg). \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}_{\mathcal{C}}'}\delta(\mathcal{C}')^2\mu_{\mathcal{C}} (\mathcal{C}')\geq\delta(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^{c}(c'_p/\varepsilon)^2}\bigg). \]
Finally, suppose that ![]() $\|\Phi ^{\leq i}_{\mathcal {C}}-\phi ^{\leq i}(\mathcal {C})\|_{U^{8}(\mathcal {C})}\geq \varepsilon$ for some
$\|\Phi ^{\leq i}_{\mathcal {C}}-\phi ^{\leq i}(\mathcal {C})\|_{U^{8}(\mathcal {C})}\geq \varepsilon$ for some ![]() $0\leq i\leq d$. Theorem 7.3 then says that there exists a polynomial
$0\leq i\leq d$. Theorem 7.3 then says that there exists a polynomial ![]() $R\in \mathbb {F}_p[x_1,\ldots,x_m,y_1,\ldots,y_m]$ of degree at most
$R\in \mathbb {F}_p[x_1,\ldots,x_m,y_1,\ldots,y_m]$ of degree at most ![]() $7$ such that
$7$ such that
By Corollary 7.2, there exists a partition ![]() $\mathscr {C}'_{\mathcal {C}}$ of
$\mathscr {C}'_{\mathcal {C}}$ of ![]() $\mathcal {C}$ into affine subspaces of the form
$\mathcal {C}$ into affine subspaces of the form ![]() $(u+V)\times (w+V)$ with
$(u+V)\times (w+V)$ with ![]() $\dim V=m'$, on each of which
$\dim V=m'$, on each of which ![]() $R$ is constant. Thus, by the Cauchy–Schwarz inequality, we have
$R$ is constant. Thus, by the Cauchy–Schwarz inequality, we have
Since
the conclusion
 \[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\phi^{\leq i}(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\phi^{\leq i}(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg) \]
\[ \sum_{\mathcal{C}'\in\mathscr{C}'_{\mathcal{C}}}\phi^{\leq i}(\mathcal{C}')^2 \mu_{\mathcal{C}}(\mathcal{C}')\geq\phi^{\leq i}(\mathcal{C})^2+\Omega\bigg(\frac{1}{\exp^c(c'_p/\varepsilon)^2}\bigg) \]
now follows.
Now we can prove Lemma 2.6.
Proof of Lemma 2.6 We proceed via an energy-increment argument, as described at the beginning of the subsection. A cell ![]() $\mathcal {C}=(u+V)\times (w+V)$ in a partition
$\mathcal {C}=(u+V)\times (w+V)$ in a partition ![]() $\mathscr {C}_j$ is said to be expired if
$\mathscr {C}_j$ is said to be expired if ![]() $\beta (\mathcal {C}),\gamma (\mathcal {C}),\delta (\mathcal {C}),$ or
$\beta (\mathcal {C}),\gamma (\mathcal {C}),\delta (\mathcal {C}),$ or ![]() $\phi ^{\leq d}(\mathcal {C})$ is less than
$\phi ^{\leq d}(\mathcal {C})$ is less than ![]() $\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/4$, and a nonexpired cell
$\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/4$, and a nonexpired cell ![]() $\mathcal {C}$ is said to be uniform if
$\mathcal {C}$ is said to be uniform if
and
for all ![]() $0\leq i\leq d$. We will denote the subset of expired cells of
$0\leq i\leq d$. We will denote the subset of expired cells of ![]() $\mathscr {C}_j$ by
$\mathscr {C}_j$ by ![]() $\mathscr {E}_j$, the subset of uniform cells by
$\mathscr {E}_j$, the subset of uniform cells by ![]() $\mathscr {U}_j$, and the subset of nonexpired, nonuniform cells by
$\mathscr {U}_j$, and the subset of nonexpired, nonuniform cells by ![]() $\mathscr {N}_j$, so that
$\mathscr {N}_j$, so that ![]() $\mathscr {E}_j,\mathscr {U}_j$, and
$\mathscr {E}_j,\mathscr {U}_j$, and ![]() $\mathscr {N}_j$ partition
$\mathscr {N}_j$ partition ![]() $\mathscr {C}_j$. For any subset
$\mathscr {C}_j$. For any subset ![]() $K\subset I_j$, we define
$K\subset I_j$, we define ![]() $\eta (K)$ to be the measure of all cells indexed by
$\eta (K)$ to be the measure of all cells indexed by ![]() $K$:
$K$:
 \[ \eta(K):=\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}\bigg(\coprod_{k\in K}\mathcal{C}_{k,j}\bigg). \]
\[ \eta(K):=\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}\bigg(\coprod_{k\in K}\mathcal{C}_{k,j}\bigg). \]
Finally, we define a sequence of integers ![]() $(m_j)_{j=0}^{\infty }$ by setting
$(m_j)_{j=0}^{\infty }$ by setting ![]() $m_0=n$ and, for every
$m_0=n$ and, for every ![]() $j>0$,
$j>0$, ![]() $m_{j}$ to be the minimum of the value of
$m_{j}$ to be the minimum of the value of ![]() $m'$ appearing in Theorem 7.1 when we take
$m'$ appearing in Theorem 7.1 when we take ![]() $m=m_{j-1}$,
$m=m_{j-1}$, ![]() $d=9$, and
$d=9$, and ![]() $t=1$ and of
$t=1$ and of ![]() $m'$ appearing in Corollary 7.2 when we take
$m'$ appearing in Corollary 7.2 when we take ![]() $m=m_{j-1}$ and
$m=m_{j-1}$ and ![]() $d=7$, so that
$d=7$, so that
for some absolute constants ![]() $0< c_1,c_2<1$.
$0< c_1,c_2<1$.
Set ![]() $\mathscr {C}_0$ to be the trivial partition
$\mathscr {C}_0$ to be the trivial partition ![]() $\{\mathbb {F}_p^n\times \mathbb {F}_p^n\}$ of
$\{\mathbb {F}_p^n\times \mathbb {F}_p^n\}$ of ![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$. Letting
$\mathbb {F}_p^n\times \mathbb {F}_p^n$. Letting ![]() $c=c_{10}$ and
$c=c_{10}$ and ![]() $c'=c'_{10,p}$ be as in Lemma 7.5, then, as long as
$c'=c'_{10,p}$ be as in Lemma 7.5, then, as long as ![]() $\eta (\mathscr {N}_j)\geq \tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/2$ and
$\eta (\mathscr {N}_j)\geq \tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/2$ and ![]() $m_{j+1}\geq 1$, there exists a refinement
$m_{j+1}\geq 1$, there exists a refinement ![]() $\mathscr {C}_{j+1}$ of
$\mathscr {C}_{j+1}$ of ![]() $\mathscr {C}_j$ such that:
$\mathscr {C}_j$ such that:
(i)
 $\dim {V_{i,j+1}}\geq m_{j+1}$ for every
$\dim {V_{i,j+1}}\geq m_{j+1}$ for every  $i\in I_{j+1}$ and
$i\in I_{j+1}$ and  $\dim {V_{i,j+1}}=m_{j+1}$ whenever
$\dim {V_{i,j+1}}=m_{j+1}$ whenever  $\mathcal {C}_{i,j+1}\in \mathscr {N}_{j+1}$; and
$\mathcal {C}_{i,j+1}\in \mathscr {N}_{j+1}$; and(ii)
 $E(\mathscr {C}_{j+1})\geq E(\mathscr {C}_j)+\Omega ( {\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)}/{d\exp ^c(c'_p/\varepsilon )^2})$.
$E(\mathscr {C}_{j+1})\geq E(\mathscr {C}_j)+\Omega ( {\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)}/{d\exp ^c(c'_p/\varepsilon )^2})$.
Indeed, suppose that ![]() $\eta (\mathscr {N}_j)\geq \tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/2$. Each cell
$\eta (\mathscr {N}_j)\geq \tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/2$. Each cell ![]() $\mathcal {C}$ in
$\mathcal {C}$ in ![]() $\mathscr {N}_j$ must be of dimension
$\mathscr {N}_j$ must be of dimension ![]() $m_j\times m_j$. By Lemmas 7.4 and 7.5, there exists a partition
$m_j\times m_j$. By Lemmas 7.4 and 7.5, there exists a partition ![]() $\mathscr {C}_{k,j+1}=(\mathcal {C}_{k,j+1})_{k\in K_{\mathcal {C}}}$ of each
$\mathscr {C}_{k,j+1}=(\mathcal {C}_{k,j+1})_{k\in K_{\mathcal {C}}}$ of each ![]() $\mathcal {C}\in \mathscr {N}_j$ such that
$\mathcal {C}\in \mathscr {N}_j$ such that
 \[ \frac{1}{4+d}\sum_{k\in K_{\mathcal{C}}}\bigg(\beta(\mathcal{C}_{k,j+1})^2+ \gamma(\mathcal{C}_{k,j+1})^2+\delta(\mathcal{C}_{k,j+1})^2+ \sum_{i=0}^d\phi^{\leq i}(\mathcal{C}_{k,j+1})^2\bigg)\mu_{\mathcal{C}}(\mathcal{C}_{k,j+1}) \]
\[ \frac{1}{4+d}\sum_{k\in K_{\mathcal{C}}}\bigg(\beta(\mathcal{C}_{k,j+1})^2+ \gamma(\mathcal{C}_{k,j+1})^2+\delta(\mathcal{C}_{k,j+1})^2+ \sum_{i=0}^d\phi^{\leq i}(\mathcal{C}_{k,j+1})^2\bigg)\mu_{\mathcal{C}}(\mathcal{C}_{k,j+1}) \]
is at least
and each ![]() $\mathcal {C}_{k,j+1}$ is of the form
$\mathcal {C}_{k,j+1}$ is of the form ![]() $(u'+V')\times (w'+V')$ with
$(u'+V')\times (w'+V')$ with ![]() $\dim {V'}=m_{j+1}\geq 1$. Taking
$\dim {V'}=m_{j+1}\geq 1$. Taking
we see that multiplying both sides of the above by ![]() $\mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(\mathcal {C})$ and summing over
$\mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(\mathcal {C})$ and summing over ![]() $\mathcal {C}\in \mathscr {N}_j$ yields
$\mathcal {C}\in \mathscr {N}_j$ yields
Since ![]() $E(\mathscr {C})\leq 1$ for all partitions
$E(\mathscr {C})\leq 1$ for all partitions ![]() $\mathscr {C}$, this iteration must terminate for some
$\mathscr {C}$, this iteration must terminate for some
at which point either ![]() $\eta (\mathscr {N}_{j_0})<\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/2$ or
$\eta (\mathscr {N}_{j_0})<\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/2$ or ![]() $m_{j_0+1}<1$. Assuming that
$m_{j_0+1}<1$. Assuming that ![]() $n\geq c_1^{-c_2^{-(j_0+1)}}$ ensures that the latter case cannot occur.
$n\geq c_1^{-c_2^{-(j_0+1)}}$ ensures that the latter case cannot occur.
Since ![]() $\eta (\mathscr {E}_j)<\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/4$, we have
$\eta (\mathscr {E}_j)<\tau \mu _{\mathbb {F}_p^n\times \mathbb {F}_p^n}(T)/4$, we have
 \[ \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}\bigg(S\cap \bigcup_{\mathcal{C}\in \mathscr{U}_{j_0}}\mathcal{C}\bigg)\geq \bigg(\sigma+\frac{\tau}{4}\bigg)\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(T). \]
\[ \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}\bigg(S\cap \bigcup_{\mathcal{C}\in \mathscr{U}_{j_0}}\mathcal{C}\bigg)\geq \bigg(\sigma+\frac{\tau}{4}\bigg)\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(T). \]
This certainly implies that
 \[ \sum_{\mathcal{C}\in\mathscr{U}_{j_0}}\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(S\cap\mathcal{C})\geq \bigg(\sigma+\frac{\tau}{4}\bigg)\sum_{\mathcal{C}\in\mathscr{U}_{j_0}} \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(T\cap\mathcal{C}), \]
\[ \sum_{\mathcal{C}\in\mathscr{U}_{j_0}}\mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(S\cap\mathcal{C})\geq \bigg(\sigma+\frac{\tau}{4}\bigg)\sum_{\mathcal{C}\in\mathscr{U}_{j_0}} \mu_{\mathbb{F}_p^n\times\mathbb{F}_p^n}(T\cap\mathcal{C}), \]
so that, by the pigeonhole principle, there exists a cell ![]() $\mathcal {C}_0$ in
$\mathcal {C}_0$ in ![]() $\mathscr {U}_{j_0}$ for which
$\mathscr {U}_{j_0}$ for which
Since ![]() $\Phi _{\mathcal {C}_0}=\coprod _{i=0}^d\Phi ^{i}_{\mathcal {C}_0}$, another application of the pigeonhole principle tells us that there exists a
$\Phi _{\mathcal {C}_0}=\coprod _{i=0}^d\Phi ^{i}_{\mathcal {C}_0}$, another application of the pigeonhole principle tells us that there exists a ![]() $0\leq i\leq d$ for which we also have the density increment
$0\leq i\leq d$ for which we also have the density increment
As noted at the beginning of this subsection,
so that the conclusion of the lemma now follows.
8. The density-increment argument
Now we can finally prove Theorem 1.2 by iterating Lemma 2.7.
Proof of Theorem 1.2 Suppose that ![]() $S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has density
$S\subset \mathbb {F}_p^n\times \mathbb {F}_p^n$ has density ![]() $\sigma$ and contains no nontrivial L-shaped configurations. Set
$\sigma$ and contains no nontrivial L-shaped configurations. Set ![]() $S_0:=S$,
$S_0:=S$, ![]() $n_0:=n$,
$n_0:=n$, ![]() $d_0=0$,
$d_0=0$, ![]() $\varepsilon _0:=1$,
$\varepsilon _0:=1$, ![]() $A_0=B_0=C_0=D_0=\mathbb {F}_p^n$, and
$A_0=B_0=C_0=D_0=\mathbb {F}_p^n$, and ![]() $\Phi _0:=\mathbb {F}_p^n\times \mathbb {F}_p^n$. Applying Lemma 2.7 repeatedly produces sequences of
$\Phi _0:=\mathbb {F}_p^n\times \mathbb {F}_p^n$. Applying Lemma 2.7 repeatedly produces sequences of ![]() $S_i$,
$S_i$, ![]() $n_i$,
$n_i$, ![]() $d_i$,
$d_i$, ![]() $\varepsilon _i$,
$\varepsilon _i$, ![]() $A_i$,
$A_i$, ![]() $B_i$,
$B_i$, ![]() $C_i$,
$C_i$, ![]() $D_i$, and
$D_i$, and ![]() $\Phi _i$, with
$\Phi _i$, with ![]() $A_i,B_i,C_i,D_i\subset \mathbb {F}_p^{n_i}$ and
$A_i,B_i,C_i,D_i\subset \mathbb {F}_p^{n_i}$ and ![]() $\Phi _i\subset A_i\times \mathbb {F}_p^{n_i}$ of the form
$\Phi _i\subset A_i\times \mathbb {F}_p^{n_i}$ of the form
where each ![]() $V_x\leq \mathbb {F}_p^{n_i}$ is a subspace of codimension
$V_x\leq \mathbb {F}_p^{n_i}$ is a subspace of codimension ![]() $d_i$, such that, on setting
$d_i$, such that, on setting
![]() $\alpha _i:=\mu _{\mathbb {F}_p^{n_i}}(A_i)$,
$\alpha _i:=\mu _{\mathbb {F}_p^{n_i}}(A_i)$, ![]() $\beta _i:=\mu _{\mathbb {F}_p^{n_i}}(B_i)$,
$\beta _i:=\mu _{\mathbb {F}_p^{n_i}}(B_i)$, ![]() $\gamma _i:=\mu _{\mathbb {F}_p^{n_i}}(C_i)$,
$\gamma _i:=\mu _{\mathbb {F}_p^{n_i}}(C_i)$, ![]() $\delta _i:=\mu _{\mathbb {F}_p^{n_i}}(D_i)$, and
$\delta _i:=\mu _{\mathbb {F}_p^{n_i}}(D_i)$, and ![]() $\rho _i:=\mu _{\mathbb {F}_p^{n_i}\times \mathbb {F}_p^{n_i}}(\Phi _i)/\alpha _i=p^{-d_i}$, we have, for each
$\rho _i:=\mu _{\mathbb {F}_p^{n_i}\times \mathbb {F}_p^{n_i}}(\Phi _i)/\alpha _i=p^{-d_i}$, we have, for each ![]() $i\geq 1$, that:
$i\geq 1$, that:
(i)
 $S_i\subset T_i$ has density
$S_i\subset T_i$ has density  $\sigma _i$ in
$\sigma _i$ in  $T_i$, where
$T_i$, where  $\sigma _i\geq \sigma _{i-1}+\Omega (\sigma ^{O(1)})$;
$\sigma _i\geq \sigma _{i-1}+\Omega (\sigma ^{O(1)})$;(ii)
 $n_i\gg n_{i-1}^{c_1^{O(\exp ^c(c'/\varepsilon _i)/(\sigma \alpha _{i-1} \beta _{i-1}\gamma _{i-1}\delta _{i-1}\rho _{i-1})^{O(1)})}}$;
$n_i\gg n_{i-1}^{c_1^{O(\exp ^c(c'/\varepsilon _i)/(\sigma \alpha _{i-1} \beta _{i-1}\gamma _{i-1}\delta _{i-1}\rho _{i-1})^{O(1)})}}$;(iii)
 $\varepsilon _i\leq (\sigma \alpha _{i}\beta _{i}\gamma _{i}\delta _{i}\rho _{i})^{O(1)}\exp (-(64/\sigma )^{O(1)})$;
$\varepsilon _i\leq (\sigma \alpha _{i}\beta _{i}\gamma _{i}\delta _{i}\rho _{i})^{O(1)}\exp (-(64/\sigma )^{O(1)})$;(iv)
 $\alpha _i,\beta _i,\gamma _i,\delta _i\gg (\sigma \alpha _{i-1}\beta _{i-1} \gamma _{i-1}\delta _{i-1}\rho _{i-1})^{O(1)}$;
$\alpha _i,\beta _i,\gamma _i,\delta _i\gg (\sigma \alpha _{i-1}\beta _{i-1} \gamma _{i-1}\delta _{i-1}\rho _{i-1})^{O(1)}$;(v)
 $d_i\leq d_{i-1}+1$;
$d_i\leq d_{i-1}+1$;(vi)
 $\|A_i-\alpha _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,
$\|A_i-\alpha _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,  $\|B_i-\beta _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,
$\|B_i-\beta _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,  $\|C_i-\gamma _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,
$\|C_i-\gamma _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,  $\|D_i-\delta _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,
$\|D_i-\delta _i\|_{U^{10}(\mathbb {F}_p^{n_i})}$,  $\|\Phi _i- \alpha _i\rho _i\|_{U^8(\mathbb {F}_p^{n_i}\times \mathbb {F}_p^{n_i})}<\varepsilon _i$; and
$\|\Phi _i- \alpha _i\rho _i\|_{U^8(\mathbb {F}_p^{n_i}\times \mathbb {F}_p^{n_i})}<\varepsilon _i$; and(vii)
 $S_i$ contains no nontrivial L-shaped configurations;
$S_i$ contains no nontrivial L-shaped configurations;
provided that
Since no set can have density larger than ![]() $1$, the lower bound (56) must fail for some
$1$, the lower bound (56) must fail for some ![]() $i=i_0+1\ll \sigma ^{-O(1)}$. Thus, there exists an absolute constant
$i=i_0+1\ll \sigma ^{-O(1)}$. Thus, there exists an absolute constant ![]() $c''>1$ such that
$c''>1$ such that
while, on the other hand,
Comparing the upper and lower bounds for ![]() $n_{i_0}$ and taking the
$n_{i_0}$ and taking the ![]() $c''$-fold iterated logarithm of both sides yields the bound in Theorem 1.2.
$c''$-fold iterated logarithm of both sides yields the bound in Theorem 1.2.
Acknowledgements
The author thanks Ben Green and Freddie Manners for helpful discussions, and Ben Green, Noah Kravitz, Terry Tao, and the anonymous referees for useful comments on earlier drafts. The author was supported by the NSF Mathematical Sciences Postdoctoral Research Fellowship Program under Grant No. DMS-1903038 and the Oswald Veblen fund, and also gratefully acknowledges the support and hospitality of the Hausdorff Institute for Mathematics, where the bulk of this paper was written.
Conflicts of Interest
None.