Published online by Cambridge University Press: 25 August 2023
Given a connected graph 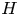 $H$ which is not a star, we show that the number of copies of
$H$ which is not a star, we show that the number of copies of 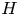 $H$ in a dense uniformly random regular graph is asymptotically Gaussian, which was not known even for
$H$ in a dense uniformly random regular graph is asymptotically Gaussian, which was not known even for 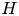 $H$ being a triangle. This addresses a question of McKay from the 2010 International Congress of Mathematicians. In fact, we prove that the behavior of the variance of the number of copies of
$H$ being a triangle. This addresses a question of McKay from the 2010 International Congress of Mathematicians. In fact, we prove that the behavior of the variance of the number of copies of 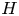 $H$ depends in a delicate manner on the occurrence and number of cycles of
$H$ depends in a delicate manner on the occurrence and number of cycles of 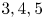 $3,4,5$ edges as well as paths of
$3,4,5$ edges as well as paths of 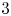 $3$ edges in
$3$ edges in 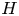 $H$. More generally, we provide control of the asymptotic distribution of certain statistics of bounded degree which are invariant under vertex permutations, including moments of the spectrum of a random regular graph. Our techniques are based on combining complex-analytic methods due to McKay and Wormald used to enumerate regular graphs with the notion of graph factors developed by Janson in the context of studying subgraph counts in
$H$. More generally, we provide control of the asymptotic distribution of certain statistics of bounded degree which are invariant under vertex permutations, including moments of the spectrum of a random regular graph. Our techniques are based on combining complex-analytic methods due to McKay and Wormald used to enumerate regular graphs with the notion of graph factors developed by Janson in the context of studying subgraph counts in 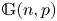 $\mathbb {G}(n,p)$.
$\mathbb {G}(n,p)$.
Sah and Sawhney were supported by NSF Graduate Research Fellowship Program DGE-2141064. Sah was supported by the PD Soros Fellowship.