Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T02:04:05.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Subconvexity for a double Dirichlet series

Part of: Exponential sums and character sums Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  07 September 2010

Valentin Blomer
Valentin Blomer*
Affiliation:
Mathematisches Institut, Bunsenstrasse 3–5, 37073 Göttingen, Germany (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

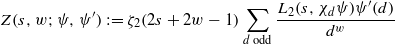
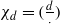For two real characters ψ,ψ′ of conductor dividing 8 define where and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to 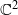possessing a group of functional equations isomorphic to D12. The convexity bound for Z(s,w;ψ,ψ′) is |sw(s+w)|1/4+ε for ℜs=ℜw=1/2. It is proved that Moreover, the following mean square Lindelöf-type bound holds: for any Y1,Y2≥1.

Keywords

multiple Dirichlet seriessubconvexityfunctional equationcharacter sums

MSC classification

Secondary: 11M41: Other Dirichlet series and zeta functions 11L40: Estimates on character sums
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 2 , March 2011 , pp. 355 - 374
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Blomer, V., On the central value of symmetric square L-functions, Math. Z. 260 (2008), 755–777.CrossRefGoogle Scholar
[2]Diaconu, A., Goldfeld, D. and Hoffstein, J., Multiple Dirichlet series and moments of zeta and L-functions, Compositio Math. 139 (2003), 297–360.CrossRefGoogle Scholar
[3]Goldfeld, D. and Hoffstein, J., Eisenstein series of -integral weight and the mean value of real Dirichlet L-series, Invent. Math. 80 (1985), 185–208.CrossRefGoogle Scholar
[4]Good, A., The square mean of Dirichlet series associated with cusp forms, Mathematika 29 (1982), 278–295.CrossRefGoogle Scholar
[5]Harcos, G., Uniform approximate functional equation for principal L-functions, Int. Math. Res. Not. 2002 (2002), 923–932; Erratum, Int. Math. Res. Not. 2004 (2004), 659–660.CrossRefGoogle Scholar
[6]Harcos, G. and Michel, P., The subconvexity problem for Rankin–Selberg L-functions and equidistribution of Heegner points. II, Invent. Math. 163 (2006), 581–655.CrossRefGoogle Scholar
[7]Heath-Brown, D. R., A mean value estimate for real character sums, Acta Arith. 72 (1995), 235–275.CrossRefGoogle Scholar
[8]Hoffstein, J. and Kontorovich, A., The first non-vanishing quadratic twist of an automorphic L -function, Preprint.Google Scholar
[9]Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
[10]Li, X., Bounds for GL(3)×GL(2) L -functions and GL(3) L -functions, Ann. of Math (2), to appear.Google Scholar
[11]Michel, Ph. and Venkatesh, A., The subconvexity problem for GL2, Publ. Math. Inst. Hautes Études Sci. 111 (2010), 172–271.CrossRefGoogle Scholar
[12]Venkatesh, A., Sparse equidistribution problems, periods bounds, and subconvexity, Ann. of Math. (2), to appear.Google Scholar
[13]Young, M., The second moment of GL(3)×GL(2) L -functions at special points, Preprint.Google Scholar