No CrossRef data available.
Article contents
Steenrod operators, the Coulomb branch and the Frobenius twist
Published online by Cambridge University Press: 04 November 2021
Abstract
We observe a fundamental relationship between Steenrod operations and the Artin–Schreier morphism. We use Steenrod's construction, together with some new geometry related to the affine Grassmannian, to prove that the quantum Coulomb branch is a Frobenius-constant quantization. We also demonstrate the corresponding result for the 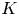 $K$-theoretic version of the quantum Coulomb branch. At the end of the paper, we investigate what our ideas produce on the categorical level. We find that they yield, after a little fiddling, a construction which corresponds, under the geometric Satake equivalence, to the Frobenius twist functor for representations of the Langlands dual group. We also describe the unfiddled answer, conditional on a conjectural ‘modular derived Satake’, and, though it is more complicated to state, it is in our opinion just as neat and even more compelling.
$K$-theoretic version of the quantum Coulomb branch. At the end of the paper, we investigate what our ideas produce on the categorical level. We find that they yield, after a little fiddling, a construction which corresponds, under the geometric Satake equivalence, to the Frobenius twist functor for representations of the Langlands dual group. We also describe the unfiddled answer, conditional on a conjectural ‘modular derived Satake’, and, though it is more complicated to state, it is in our opinion just as neat and even more compelling.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
This work was carried out at, and with the generous support of, MIT. Thanks also to AIM and the organizers of the AIM workshop on sheaves and modular representations of reductive groups, March 28 to April 1, 2016, where many of the ideas in this paper began.



