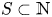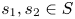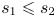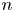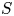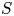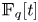1. Introduction
A set ![]() $S$ of natural numbers is called a Sidon set, or a Sidon sequence, if all the sums
$S$ of natural numbers is called a Sidon set, or a Sidon sequence, if all the sums ![]() $s_1+s_2$, for
$s_1+s_2$, for ![]() $s_1, s_2\in S$,
$s_1, s_2\in S$, ![]() $s_1\leqslant s_2$, are distinct. Sidon sequences are named after Simon Sidon, who in 1932 asked Erdős about the possible growth rate of such sequences. We write
$s_1\leqslant s_2$, are distinct. Sidon sequences are named after Simon Sidon, who in 1932 asked Erdős about the possible growth rate of such sequences. We write
Erdős observed that the greedy algorithm generates a Sidon sequence ![]() $S$ with
$S$ with ![]() $S(x) \gg x^{1/3}$. He also conjectured that, for every
$S(x) \gg x^{1/3}$. He also conjectured that, for every ![]() $\varepsilon >0$, there is a Sidon sequence
$\varepsilon >0$, there is a Sidon sequence ![]() $S$ with
$S$ with ![]() $S(x) \gg x^{1/2-\varepsilon }$ (see [Reference ErdősErd81]). In some sense, this would be best possible, as Erdős showed that any Sidon sequence
$S(x) \gg x^{1/2-\varepsilon }$ (see [Reference ErdősErd81]). In some sense, this would be best possible, as Erdős showed that any Sidon sequence ![]() $S$ satisfies
$S$ satisfies
for infinitely many ![]() $x$ (see [Reference Halberstam and RothHR83, Theorem 8]). The lower bound was improved in 1981 by Ajtai, Komlós and Szemerédi [Reference Ajtai, Komlós and SzemerédiAKS81], who proved the existence of a Sidon sequence
$x$ (see [Reference Halberstam and RothHR83, Theorem 8]). The lower bound was improved in 1981 by Ajtai, Komlós and Szemerédi [Reference Ajtai, Komlós and SzemerédiAKS81], who proved the existence of a Sidon sequence ![]() $S$ with
$S$ with
using graph-theoretic tools. In a 1998 landmark paper, Ruzsa [Reference RuzsaRuz98] used the fact that the primes form a ‘multiplicative Sidon set’ to construct a Sidon sequence ![]() $S$ with
$S$ with
This is still the best-known lower bound: improving the exponent ![]() $\sqrt {2}-1 \approx 0.4142\ldots$ would be a major achievement.
$\sqrt {2}-1 \approx 0.4142\ldots$ would be a major achievement.
It is worth mentioning that much more is known about finite Sidon sets. In particular, the maximal size of a Sidon subset of ![]() $\{1,2,\ldots, n\}$ is
$\{1,2,\ldots, n\}$ is ![]() $n^{1/2}+O(n^{1/4})$ (see Halberstam and Roth [Reference Halberstam and RothHR83, Chapter I, § 3] for detailed references).
$n^{1/2}+O(n^{1/4})$ (see Halberstam and Roth [Reference Halberstam and RothHR83, Chapter I, § 3] for detailed references).
Sidon sequences have become classical objects of interest in arithmetic combinatorics. It is natural to study the properties of the sumset ![]() $S+S := \{s_1+s_2:s_1, s_2\in S\}$, or more generally of the
$S+S := \{s_1+s_2:s_1, s_2\in S\}$, or more generally of the ![]() $k$th iterated sumset
$k$th iterated sumset ![]() ${kS := \underbrace {S+S+\cdots +S}_{k \text { times}}}$, when
${kS := \underbrace {S+S+\cdots +S}_{k \text { times}}}$, when ![]() $S$ is a Sidon sequence.
$S$ is a Sidon sequence.
A subset ![]() $A\subset {\mathbb {N}}$ is called an asymptotic basis of order
$A\subset {\mathbb {N}}$ is called an asymptotic basis of order ![]() $k$ if
$k$ if ![]() $ {\mathbb {N}} \setminus kA$ is finite. In other words,
$ {\mathbb {N}} \setminus kA$ is finite. In other words, ![]() $A$ is an asymptotic basis of order
$A$ is an asymptotic basis of order ![]() $k$ if every sufficiently large integer can be written as the sum of
$k$ if every sufficiently large integer can be written as the sum of ![]() $k$ elements of
$k$ elements of ![]() $A$. Many well-known problems can be restated as follows: for a given set
$A$. Many well-known problems can be restated as follows: for a given set ![]() $A$, what is the smallest
$A$, what is the smallest ![]() $k$ such that
$k$ such that ![]() $A$ is an asymptotic basis of order
$A$ is an asymptotic basis of order ![]() $k$? If
$k$? If ![]() $A$ is the set of primes, this is essentially Goldbach's conjecture, whereas if
$A$ is the set of primes, this is essentially Goldbach's conjecture, whereas if ![]() $A$ is the set of perfect
$A$ is the set of perfect ![]() $d$th powers, this is a variant of Waring's problem.
$d$th powers, this is a variant of Waring's problem.
In [Reference Erdős, Sárközy and SósESS94a, Problem 14] and [Reference Erdős, Sárközy and SósESS94b, Problem 8], Erdős, Sárközy and Sós asked the following question.
Problem 1.1 Does there exist a Sidon sequence ![]() $S$ which is an asymptotic basis of order 3?
$S$ which is an asymptotic basis of order 3?
This problem also appears in Erdős [Reference ErdősErd98, p. 212] and Sárközy [Reference SárközySár01, Problem 32].Footnote 1 In his paper [Reference ErdősErd98], Erdős describes Problem 1.1 as ‘an old problem of Nathanson and myself’.
It is easy to see that no Sidon sequence can be an asymptotic basis of order ![]() $2$. In fact, Erdős, Sárközy and Sós [Reference Erdős, Sárközy and SósESS95] proved that for any Sidon set
$2$. In fact, Erdős, Sárközy and Sós [Reference Erdős, Sárközy and SósESS95] proved that for any Sidon set ![]() $S\subset \{1, 2, \ldots, n\}$, the sumset
$S\subset \{1, 2, \ldots, n\}$, the sumset ![]() $S+S$ cannot contain
$S+S$ cannot contain ![]() $\geqslant Cn^{1/2}$ consecutive integers, where
$\geqslant Cn^{1/2}$ consecutive integers, where ![]() $C$ is an absolute constant. Thus, the constant ‘
$C$ is an absolute constant. Thus, the constant ‘![]() $3$’ in Problem 1.1 can certainly not be improved.
$3$’ in Problem 1.1 can certainly not be improved.
In this article, we settle Problem 1.1 by proving the existence of a Sidon sequence ![]() $S$ which is also an asymptotic basis of order
$S$ which is also an asymptotic basis of order ![]() $3$.
$3$.
A number of partial results have been previously obtained in the direction of Problem 1.1.

To make sense of the last row, we recall that a set ![]() $S\subset {\mathbb {N}}$ is an asymptotic basis of order
$S\subset {\mathbb {N}}$ is an asymptotic basis of order ![]() $3+\varepsilon$ if, for every
$3+\varepsilon$ if, for every ![]() $\varepsilon >0$, every sufficiently large integer
$\varepsilon >0$, every sufficiently large integer ![]() $n$ can be written as the sum of four elements of
$n$ can be written as the sum of four elements of ![]() $S$, with one of them
$S$, with one of them ![]() $\leqslant n^{\varepsilon }$. Our solution to Problem 1.1 also generalises another result of Cilleruelo [Reference CillerueloCil15, Theorem 1.2], which states that there is an asymptotic basis
$\leqslant n^{\varepsilon }$. Our solution to Problem 1.1 also generalises another result of Cilleruelo [Reference CillerueloCil15, Theorem 1.2], which states that there is an asymptotic basis ![]() $S$ of order
$S$ of order ![]() $3$ such that every integer
$3$ such that every integer ![]() $n$ can be represented in at most two different ways as a sum of two elements of
$n$ can be represented in at most two different ways as a sum of two elements of ![]() $S$. Finally, Kiss and Sándor [Reference Kiss and SándorKS23] showed the existence of a Sidon sequence
$S$. Finally, Kiss and Sándor [Reference Kiss and SándorKS23] showed the existence of a Sidon sequence ![]() $S\subset {\mathbb {N}}$ whose
$S\subset {\mathbb {N}}$ whose ![]() $3$-fold sumset
$3$-fold sumset ![]() $S+S+S$ has lower asymptotic density
$S+S+S$ has lower asymptotic density ![]() $>0.0064$.Footnote 2
$>0.0064$.Footnote 2
The results in [Reference CillerueloCil15, Reference KissKis10, Reference Kiss, Rozgonyi and SándorKRS14, Reference Kiss and SándorKS23] quoted above all use some variant of the probabilistic method. The starting point of all these approaches is to consider a random subset ![]() $S$ of
$S$ of ![]() $ {\mathbb {N}}$ where each
$ {\mathbb {N}}$ where each ![]() $n\in {\mathbb {N}}$ is chosen to be in
$n\in {\mathbb {N}}$ is chosen to be in ![]() $S$, independently, with some probability
$S$, independently, with some probability ![]() $p(n)$: a typical choice is
$p(n)$: a typical choice is ![]() $p(n) = n^{-\gamma }$ for some
$p(n) = n^{-\gamma }$ for some ![]() $\gamma >0$. In order for
$\gamma >0$. In order for ![]() $S$ to resemble a Sidon sequence (i.e. to be able to use the alteration method), it is necessary to have something roughly like
$S$ to resemble a Sidon sequence (i.e. to be able to use the alteration method), it is necessary to have something roughly like ![]() $p(n) \ll n^{-2/3}$. In [Reference CillerueloCil15, Reference KissKis10, Reference Kiss, Rozgonyi and SándorKRS14], the authors choose
$p(n) \ll n^{-2/3}$. In [Reference CillerueloCil15, Reference KissKis10, Reference Kiss, Rozgonyi and SándorKRS14], the authors choose ![]() $p(n) = n^{-\gamma }$ for some
$p(n) = n^{-\gamma }$ for some ![]() $\gamma <2/3$, while for [Reference Kiss and SándorKS23] they choose
$\gamma <2/3$, while for [Reference Kiss and SándorKS23] they choose ![]() $p(n) = c n^{-2/3}$ for some optimised constant
$p(n) = c n^{-2/3}$ for some optimised constant ![]() $c>0$. However, for such choices of
$c>0$. However, for such choices of ![]() $p(n)$, the set
$p(n)$, the set ![]() $S$ will almost surely not be an asymptotic basis of order
$S$ will almost surely not be an asymptotic basis of order ![]() $3$ (this follows from [Reference GoguelGog75, Satz B]). Hence, it seems that purely probabilistic approaches are of little use for addressing Problem 1.1.
$3$ (this follows from [Reference GoguelGog75, Satz B]). Hence, it seems that purely probabilistic approaches are of little use for addressing Problem 1.1.
In order to obtain an asymptotic basis of order ![]() $3$, it is more promising to start from the Sidon sequence of Ruzsa mentioned previously [Reference RuzsaRuz98], as it is much denser than the Sidon sets obtained by the probabilistic method.
$3$, it is more promising to start from the Sidon sequence of Ruzsa mentioned previously [Reference RuzsaRuz98], as it is much denser than the Sidon sets obtained by the probabilistic method.
The underlying idea behind Ruzsa's construction is to consider an infinite set of primes ![]() $\mathcal {P}$, and for each
$\mathcal {P}$, and for each ![]() $p\in \mathcal {P}$, to define a natural number
$p\in \mathcal {P}$, to define a natural number ![]() $n_p$ that ‘behaves like a logarithm of
$n_p$ that ‘behaves like a logarithm of ![]() $p$’, so that an equality
$p$’, so that an equality ![]() $n_{p_1} + n_{p_2} = n_{p_3} + n_{p_4}$ only holds if
$n_{p_1} + n_{p_2} = n_{p_3} + n_{p_4}$ only holds if ![]() $p_1p_2 = p_3p_4$. Since the primes form a multiplicative Sidon set, we get
$p_1p_2 = p_3p_4$. Since the primes form a multiplicative Sidon set, we get ![]() $\{p_1, p_2\} = \{p_3, p_4\}$, so the set
$\{p_1, p_2\} = \{p_3, p_4\}$, so the set ![]() $S := \{n_p : p\in \mathcal {P}\}$ has the Sidon property. In his original paper, Ruzsa defined
$S := \{n_p : p\in \mathcal {P}\}$ has the Sidon property. In his original paper, Ruzsa defined ![]() $n_p$ in terms of the binary expansion of the real number
$n_p$ in terms of the binary expansion of the real number ![]() $\log _b{p}$ (for some
$\log _b{p}$ (for some ![]() $b\in {\mathbb {R}}^{>1}$) by concatenating certain blocks of digits of
$b\in {\mathbb {R}}^{>1}$) by concatenating certain blocks of digits of ![]() $\log _b{p}$ to obtain a natural number.
$\log _b{p}$ to obtain a natural number.
Cilleruelo [Reference CillerueloCil14] proposed a neat variant of Ruzsa's construction, where the real logarithm is replaced by a family of discrete logarithms. Fix an increasing sequence ![]() $\ell _1, \ell _2, \ldots$ of primes
$\ell _1, \ell _2, \ldots$ of primes ![]() $\ell _i\not \in \mathcal {P}$ and choose for each
$\ell _i\not \in \mathcal {P}$ and choose for each ![]() $i$ a primitive root
$i$ a primitive root ![]() $\omega _i$ modulo
$\omega _i$ modulo ![]() $\ell _i$. Write
$\ell _i$. Write ![]() $\log _{\ell _i, \omega _i}(p)$ for the unique
$\log _{\ell _i, \omega _i}(p)$ for the unique ![]() $e\in \{0, 1, \ldots, \ell _i-2\}$ such that
$e\in \{0, 1, \ldots, \ell _i-2\}$ such that ![]() $\omega _i^e \equiv p \pmod {\ell _i}$. Cilleruelo defined
$\omega _i^e \equiv p \pmod {\ell _i}$. Cilleruelo defined ![]() $n_p$ by encoding many of these discrete logarithms
$n_p$ by encoding many of these discrete logarithms ![]() $\log _{\ell _i, \omega _i}(p)$ into a single natural number, using a suitable base expansion. Now, an equality of the form
$\log _{\ell _i, \omega _i}(p)$ into a single natural number, using a suitable base expansion. Now, an equality of the form ![]() $n_{p_1} + n_{p_2} = n_{p_3} + n_{p_4}$ implies that
$n_{p_1} + n_{p_2} = n_{p_3} + n_{p_4}$ implies that
for many values of ![]() $i$, and thus
$i$, and thus ![]() $p_1p_2 \equiv p_3p_4 \pmod {\ell _i}$ for many
$p_1p_2 \equiv p_3p_4 \pmod {\ell _i}$ for many ![]() $i$. With the appropriate quantification, this is only possible if
$i$. With the appropriate quantification, this is only possible if ![]() $p_1p_2 = p_3p_4$, which forces
$p_1p_2 = p_3p_4$, which forces ![]() $\{p_1, p_2\} = \{p_3, p_4\}$ as before.
$\{p_1, p_2\} = \{p_3, p_4\}$ as before.
Neither Ruzsa's nor Cilleruelo's construction constitutes an asymptotic basis of order ![]() $3$. There is an obvious obstruction, which is intrinsically tied to the way the information about
$3$. There is an obvious obstruction, which is intrinsically tied to the way the information about ![]() $p$ is encoded in
$p$ is encoded in ![]() $n_p$. For the readers familiar with Ruzsa's construction, the reason is due to the presence of zeros between the blocks of digits of
$n_p$. For the readers familiar with Ruzsa's construction, the reason is due to the presence of zeros between the blocks of digits of ![]() $\log _b{p}$ within
$\log _b{p}$ within ![]() $n_p$. These zeros cannot be removed, for this would destroy the Sidon property of
$n_p$. These zeros cannot be removed, for this would destroy the Sidon property of ![]() $S$. Cilleruelo's construction suffers from a similar drawback.
$S$. Cilleruelo's construction suffers from a similar drawback.
Our point of departure is Cilleruelo's construction. To avoid the issue raised in the previous paragraph, we replace the zeros in the encoding of ![]() $n_p$ with random numbers chosen from a carefully designed set
$n_p$ with random numbers chosen from a carefully designed set ![]() $A$ (see Lemma 3.1 and Definition 3.3). The remaining task is to prove that our modified Cilleruelo construction produces an asymptotic basis of order
$A$ (see Lemma 3.1 and Definition 3.3). The remaining task is to prove that our modified Cilleruelo construction produces an asymptotic basis of order ![]() $3$. Eventually, this reduces to information about the distribution of products of three primes in arithmetic progressions.
$3$. Eventually, this reduces to information about the distribution of products of three primes in arithmetic progressions.
However, the kind of information we would need is not remotely within reach of our current knowledge of prime numbers. We would need something along the lines of Montgomery's conjecture, a far-reaching generalisation of the generalised Riemann hypothesis. Montgomery's conjecture [Reference Iwaniec and KowalskiIK04, Eq. (17.5), p. 419] states that, for every ![]() $\varepsilon >0$,
$\varepsilon >0$,
 \begin{equation} \psi(x;q,a) := \sum_{\substack{n\leqslant x\\ n\equiv a\,(\mathrm{mod}\ q)}} \Lambda(n) = \frac{x}{\varphi(q)} + O_{\varepsilon}\big(q^{-1/2}x^{1/2+\varepsilon}\big) \end{equation}
\begin{equation} \psi(x;q,a) := \sum_{\substack{n\leqslant x\\ n\equiv a\,(\mathrm{mod}\ q)}} \Lambda(n) = \frac{x}{\varphi(q)} + O_{\varepsilon}\big(q^{-1/2}x^{1/2+\varepsilon}\big) \end{equation}
uniformly in ![]() $x, q\geqslant 1$ and
$x, q\geqslant 1$ and ![]() $(a, q)=1$. This implies the asymptotic formula
$(a, q)=1$. This implies the asymptotic formula ![]() $\psi (x;q,a) \sim x/\varphi (q)$ uniformly in the residue class and the modulus, provided that
$\psi (x;q,a) \sim x/\varphi (q)$ uniformly in the residue class and the modulus, provided that ![]() $q\leqslant x^{1-\varepsilon }$. We would need a similar (suitably normalised) statement, with the triple convolution
$q\leqslant x^{1-\varepsilon }$. We would need a similar (suitably normalised) statement, with the triple convolution ![]() $\Lambda *\Lambda *\Lambda$ in place of the von Mangoldt function
$\Lambda *\Lambda *\Lambda$ in place of the von Mangoldt function ![]() $\Lambda$.
$\Lambda$.
Cilleruelo [Reference CillerueloCil14, § 4] observed that his construction works equally well over ![]() $\mathbb {F}_q[t]$. Let
$\mathbb {F}_q[t]$. Let ![]() $\mathcal {F}$ be a set of irreducible monic polynomials in
$\mathcal {F}$ be a set of irreducible monic polynomials in ![]() $\mathbb {F}_q[t]$. Fix a sequence
$\mathbb {F}_q[t]$. Fix a sequence ![]() $(g_i)$ of irreducible monic polynomials not in
$(g_i)$ of irreducible monic polynomials not in ![]() $\mathcal {F}$, and for each
$\mathcal {F}$, and for each ![]() $g_i$, choose a generator
$g_i$, choose a generator ![]() $\omega _i$ of
$\omega _i$ of ![]() $(\mathbb {F}_q[t]/(g_i))^{\times }$. For
$(\mathbb {F}_q[t]/(g_i))^{\times }$. For ![]() $f\in \mathcal {F}$, write
$f\in \mathcal {F}$, write ![]() $\log _{g_i, \omega _i}(f)$ for the unique integer
$\log _{g_i, \omega _i}(f)$ for the unique integer ![]() $e\in \{0, 1, \ldots, q^{\deg g_i}-1\}$ such that
$e\in \{0, 1, \ldots, q^{\deg g_i}-1\}$ such that ![]() $\omega _i^{e} \equiv f\pmod {g_i}$. As before, one can define an integer
$\omega _i^{e} \equiv f\pmod {g_i}$. As before, one can define an integer ![]() $n_f$ in terms of many such integers
$n_f$ in terms of many such integers ![]() $\log _{g_i, \omega _i}(f)$, so that
$\log _{g_i, \omega _i}(f)$, so that ![]() $S := \{n_f : f\in \mathcal {F}\}$ is a Sidon sequence. It is important to remember that
$S := \{n_f : f\in \mathcal {F}\}$ is a Sidon sequence. It is important to remember that ![]() $S$ is a Sidon sequence of integers, even if
$S$ is a Sidon sequence of integers, even if ![]() $\mathcal {F}$ is a subset of
$\mathcal {F}$ is a subset of ![]() $\mathbb {F}_q[t]$.
$\mathbb {F}_q[t]$.
The final and crucial ingredient to our proof is the remarkable work of Sawin [Reference SawinSaw21], who proved Montgomery-type results for ‘factorisation functions’ in ![]() $\mathbb {F}_q[t]$, a class of arithmetic functions that encompasses (the
$\mathbb {F}_q[t]$, a class of arithmetic functions that encompasses (the ![]() $\mathbb {F}_q[t]$-version of) the von Mangoldt function and its convolutions. For example, [Reference SawinSaw21, Theorem 1.2] implies that, for all
$\mathbb {F}_q[t]$-version of) the von Mangoldt function and its convolutions. For example, [Reference SawinSaw21, Theorem 1.2] implies that, for all ![]() $\varepsilon >0$, there is some
$\varepsilon >0$, there is some ![]() $q_0(\varepsilon )$ such that, for all prime powers
$q_0(\varepsilon )$ such that, for all prime powers ![]() $q\geqslant q_0(\varepsilon )$, the analogue of Montgomery's conjecture (1) holds over
$q\geqslant q_0(\varepsilon )$, the analogue of Montgomery's conjecture (1) holds over ![]() $\mathbb {F}_q[t]$ (for squarefree moduli), i.e.
$\mathbb {F}_q[t]$ (for squarefree moduli), i.e.
 \begin{equation} \sum_{\substack{f\in \mathbb{F}_q[t]\\ f\text{ monic of degree }n\\ f\equiv a\,(\mathrm{mod}\ g)}} \Lambda(f) = \frac{q^n}{\varphi(g)} + O\big((q^{\deg g})^{-1/2}(q^n)^{1/2+\varepsilon}\big) \end{equation}
\begin{equation} \sum_{\substack{f\in \mathbb{F}_q[t]\\ f\text{ monic of degree }n\\ f\equiv a\,(\mathrm{mod}\ g)}} \Lambda(f) = \frac{q^n}{\varphi(g)} + O\big((q^{\deg g})^{-1/2}(q^n)^{1/2+\varepsilon}\big) \end{equation}
uniformly in the modulus ![]() $g$ (squarefree monic polynomial) and in the residue class
$g$ (squarefree monic polynomial) and in the residue class ![]() $a$, with
$a$, with ![]() ${(a,g)=1}$. Sawin's work relies on deep algebraic geometry methods, including sheaf cohomology, the characteristic cycle, vanishing cycles theory and perverse sheaves. We use a bound similar to (2) for the triple convolution
${(a,g)=1}$. Sawin's work relies on deep algebraic geometry methods, including sheaf cohomology, the characteristic cycle, vanishing cycles theory and perverse sheaves. We use a bound similar to (2) for the triple convolution ![]() $\Lambda *\Lambda *\Lambda$ (see Lemma 5.2). With this powerful result, we are able to prove that our modified Cilleruelo sequence is an asymptotic basis of order
$\Lambda *\Lambda *\Lambda$ (see Lemma 5.2). With this powerful result, we are able to prove that our modified Cilleruelo sequence is an asymptotic basis of order ![]() $3$, thereby solving Problem 1.1.
$3$, thereby solving Problem 1.1.
To conclude this introduction, we mention an application of our work to the study of ![]() $B_h[1]$ sequences. A set
$B_h[1]$ sequences. A set ![]() $S\subset {\mathbb {N}}$ is said to be
$S\subset {\mathbb {N}}$ is said to be ![]() $B_h[g]$ set if every positive integer can be written as the sum of
$B_h[g]$ set if every positive integer can be written as the sum of ![]() $h$ terms from
$h$ terms from ![]() $S$ at most
$S$ at most ![]() $g$ different ways. For any
$g$ different ways. For any ![]() $h\geqslant 2$, with the probabilistic method, Kiss and Sándor successively showed the existence of a
$h\geqslant 2$, with the probabilistic method, Kiss and Sándor successively showed the existence of a ![]() $B_h[1]$ set which is an asymptotic basis of order
$B_h[1]$ set which is an asymptotic basis of order ![]() $2h+1$ (see [Reference Kiss and SándorKS21]), then
$2h+1$ (see [Reference Kiss and SándorKS21]), then ![]() $2h$ (see [Reference Kiss and SándorKS22]). A simple modification of our proof should establish the existence of a
$2h$ (see [Reference Kiss and SándorKS22]). A simple modification of our proof should establish the existence of a ![]() $B_h[1]$ set which is an asymptotic basis of order
$B_h[1]$ set which is an asymptotic basis of order ![]() $2h-1$, for
$2h-1$, for ![]() $h\geqslant 2$, thus answering a question of Kiss and Sándor [Reference Kiss and SándorKS21, Reference Kiss and SándorKS22].
$h\geqslant 2$, thus answering a question of Kiss and Sándor [Reference Kiss and SándorKS21, Reference Kiss and SándorKS22].
2. Notation
The sumset of two sets ![]() $A,B\subset {\mathbb {Z}}$ is
$A,B\subset {\mathbb {Z}}$ is ![]() $A + B := \{a+b : a\in A, \, b\in B\}$. We write
$A + B := \{a+b : a\in A, \, b\in B\}$. We write ![]() $f \ll g$ or
$f \ll g$ or ![]() $f = O(g)$ if
$f = O(g)$ if ![]() $\big |f\big | \leqslant C g$ for some absolute constant
$\big |f\big | \leqslant C g$ for some absolute constant ![]() $C>0$. If instead
$C>0$. If instead ![]() $C$ depends on a parameter
$C$ depends on a parameter ![]() $\theta$, we write
$\theta$, we write ![]() $f \ll _{\theta } g$ or
$f \ll _{\theta } g$ or ![]() $f = O_{\theta }(g)$.
$f = O_{\theta }(g)$.
For ![]() $b\geqslant 1$ and
$b\geqslant 1$ and ![]() $a\in {\mathbb {Z}}$, we write
$a\in {\mathbb {Z}}$, we write ![]() $\big [a \ \mathrm {mod}\ b \big ]$ for the unique integer
$\big [a \ \mathrm {mod}\ b \big ]$ for the unique integer ![]() $n$ satisfying
$n$ satisfying ![]() $0\leqslant n < b$ and
$0\leqslant n < b$ and ![]() ${n\equiv a \pmod b}$.
${n\equiv a \pmod b}$.
Definition 2.1 (Generalised base)
Let ![]() $\boldsymbol {b} = (b_1, b_2, \ldots )$ be an infinite sequence of integers
$\boldsymbol {b} = (b_1, b_2, \ldots )$ be an infinite sequence of integers ![]() $\geqslant 2$. For any
$\geqslant 2$. For any ![]() $n\geqslant 1$ and any
$n\geqslant 1$ and any ![]() $x_1, \ldots, x_n \in {\mathbb {Z}}$, we write
$x_1, \ldots, x_n \in {\mathbb {Z}}$, we write
Any ![]() $m\in {\mathbb {Z}}^{\geqslant 1}$ can be uniquely represented as
$m\in {\mathbb {Z}}^{\geqslant 1}$ can be uniquely represented as ![]() $m = \overline {x_n \ldots x_1}^{\boldsymbol {b}}$ for some
$m = \overline {x_n \ldots x_1}^{\boldsymbol {b}}$ for some ![]() $0\leqslant x_i< b_i$ with
$0\leqslant x_i< b_i$ with ![]() $x_n\neq 0$. Recall, however, that the notation
$x_n\neq 0$. Recall, however, that the notation ![]() $\overline {x_n \ldots x_1}^{\boldsymbol {b}}$ is defined for arbitrary integers
$\overline {x_n \ldots x_1}^{\boldsymbol {b}}$ is defined for arbitrary integers ![]() $x_i$: we do not always require
$x_i$: we do not always require ![]() $0\leqslant x_i< b_i$.
$0\leqslant x_i< b_i$.
3. Construction
The following lemma is a slight strengthening of the statement that, for any sufficiently large ![]() $p$, there exists a set
$p$, there exists a set ![]() $A\subset {\mathbb {Z}}/p {\mathbb {Z}}$ such that
$A\subset {\mathbb {Z}}/p {\mathbb {Z}}$ such that ![]() $A$ and
$A$ and ![]() $A+A$ are disjoint, and moreover
$A+A$ are disjoint, and moreover ![]() $A+A+A = {\mathbb {Z}}/p {\mathbb {Z}}$.
$A+A+A = {\mathbb {Z}}/p {\mathbb {Z}}$.
Lemma 3.1 For every sufficiently large prime ![]() $p$, there is a set
$p$, there is a set ![]() $A \subset \{1, 2, \ldots, \lfloor p/2 \rfloor - 1\}$ such that:
$A \subset \{1, 2, \ldots, \lfloor p/2 \rfloor - 1\}$ such that:
(i) the sets
 $A$ and
$A$ and  $A+A+\{0, 1\}$ are disjoint;
$A+A+\{0, 1\}$ are disjoint;(ii)
 $A+A+A$ contains
$A+A+A$ contains  $p+2$ consecutive integers.
$p+2$ consecutive integers.
It turns out that we only need to use the existence of a single pair ![]() $(p, A)$ with these properties. Lemma 3.1 can be shown by the alteration method in probabilistic combinatorics. We provide a detailed proof in Appendix A.
$(p, A)$ with these properties. Lemma 3.1 can be shown by the alteration method in probabilistic combinatorics. We provide a detailed proof in Appendix A.
For the remainder of this paper, we fix a pair ![]() $(p, A)$ satisfying the conclusion of Lemma 3.1. In particular,
$(p, A)$ satisfying the conclusion of Lemma 3.1. In particular, ![]() $p$ should be thought of as an absolute constant. Let
$p$ should be thought of as an absolute constant. Let ![]() $c = 0.35$, the point is that
$c = 0.35$, the point is that
Let ![]() $C_0 > 100p$ be a large absolute constant that will be chosen later.
$C_0 > 100p$ be a large absolute constant that will be chosen later.
Definition 3.2 ( $\mathcal {P}_{d}$,
$\mathcal {P}_{d}$,  $g_i$,
$g_i$,  $\omega _i$,
$\omega _i$,  $\mathcal {F}_k$,
$\mathcal {F}_k$,  $\mathcal {F}$)
$\mathcal {F}$)
Let ![]() $q\geqslant C_0$ be a prime (or a prime power). Let
$q\geqslant C_0$ be a prime (or a prime power). Let ![]() $\mathcal {P}_{d}$ be the set of irreducible monic polynomials
$\mathcal {P}_{d}$ be the set of irreducible monic polynomials ![]() $f\in \mathbb {F}_q[t]$ of degree
$f\in \mathbb {F}_q[t]$ of degree ![]() $d$. Recall the standard formula of Gauss
$d$. Recall the standard formula of Gauss
 \begin{equation} |\mathcal{P}_{d}| = \frac{1}{d}\sum_{e \mid d} \mu \biggl(\frac{d}{e}\biggr) q^{e} = \frac{q^d}{d} + O(q^{d/2}). \end{equation}
\begin{equation} |\mathcal{P}_{d}| = \frac{1}{d}\sum_{e \mid d} \mu \biggl(\frac{d}{e}\biggr) q^{e} = \frac{q^d}{d} + O(q^{d/2}). \end{equation} For ![]() $i\geqslant 1$, let
$i\geqslant 1$, let ![]() $g_i$ be an arbitrary element of
$g_i$ be an arbitrary element of ![]() $\mathcal {P}_{2i-1}$, and fix an arbitrary generator
$\mathcal {P}_{2i-1}$, and fix an arbitrary generator ![]() $\omega _i$ of
$\omega _i$ of ![]() $(\mathbb {F}_q[t]/(g_i))^{\times }$.
$(\mathbb {F}_q[t]/(g_i))^{\times }$.
For ![]() $k\geqslant C_0$, let
$k\geqslant C_0$, let
Let ![]() $\mathcal {F} := \bigcup _{k\geqslant C_0} \mathcal {F}_k$.
$\mathcal {F} := \bigcup _{k\geqslant C_0} \mathcal {F}_k$.
We work in the generalised base ![]() $\boldsymbol {b} = (b_1, b_2, \ldots )$ where
$\boldsymbol {b} = (b_1, b_2, \ldots )$ where
 \begin{equation} b_i = \begin{cases} q^{i}-1 & i\text{ odd},\\ p & i \text{ even.} \end{cases} \end{equation}
\begin{equation} b_i = \begin{cases} q^{i}-1 & i\text{ odd},\\ p & i \text{ even.} \end{cases} \end{equation}Definition 3.3 ( $e_i$,
$e_i$,  $r_i$,
$r_i$,  $s$,
$s$,  $n_f$,
$n_f$,  $S$)
$S$)
Let ![]() $k\geqslant C_0$ and let
$k\geqslant C_0$ and let ![]() $f\in \mathcal {F}_k$. We associate to
$f\in \mathcal {F}_k$. We associate to ![]() $f$ a positive integer
$f$ a positive integer ![]() $n_f$ as follows.
$n_f$ as follows.
• For
 $1\leqslant i\leqslant k$, let
$1\leqslant i\leqslant k$, let  $e_i(f)$ be the unique integer such that
$e_i(f)$ be the unique integer such that  $0\leqslant e_i(f)< b_{2i-1} = q^{2 i-1}-1$ and
$0\leqslant e_i(f)< b_{2i-1} = q^{2 i-1}-1$ and
 \[ \omega_i^{e_i(f)} \equiv f \pmod {g_i}. \]
\[ \omega_i^{e_i(f)} \equiv f \pmod {g_i}. \]
• Let
 $r_1(f), \ldots, r_k(f)$ be a sequence of independent and identically distributed (i.i.d.) random variables, each uniformly distributed on
$r_1(f), \ldots, r_k(f)$ be a sequence of independent and identically distributed (i.i.d.) random variables, each uniformly distributed on  $A$ (in particular,
$A$ (in particular,  $1\leqslant r_i(f) \leqslant p/2-1$).
$1\leqslant r_i(f) \leqslant p/2-1$).• Let
 $s(f)$ be an integer chosen uniformly at random in the set
$s(f)$ be an integer chosen uniformly at random in the set  $\{1, 2, \ldots, q^{3k}\}$.
$\{1, 2, \ldots, q^{3k}\}$.
It is understood that the family of all random variables ![]() $r_i(f)$ and
$r_i(f)$ and ![]() $s(f)$ (over all choices of
$s(f)$ (over all choices of ![]() $f$ and
$f$ and ![]() $i$) is independent.
$i$) is independent.
We define ![]() $n_f$ to be the integer
$n_f$ to be the integer
omitting the dependence of each digit on ![]() $f$ for conciseness. To be explicit,
$f$ for conciseness. To be explicit,
with ![]() $b_i$ as in (4).Footnote 3
$b_i$ as in (4).Footnote 3
Finally, we define ![]() $S = \{n_f : f\in \mathcal {F}\}$.
$S = \{n_f : f\in \mathcal {F}\}$.
We show that, with probability ![]() $1$, the elements of
$1$, the elements of ![]() $S$ form a Sidon sequence and an asymptotic basis of order
$S$ form a Sidon sequence and an asymptotic basis of order ![]() $3$.
$3$.
Lemma 3.4
(i) Let
 $f\in \mathcal {F}_k$. Then
$f\in \mathcal {F}_k$. Then  $n_f = q^{k^2+O(k)}$.
$n_f = q^{k^2+O(k)}$.(ii) Let
 $f_1, f_2\in \mathcal {F}$ be such that
$f_1, f_2\in \mathcal {F}$ be such that  $n_{f_1} = n_{f_2}$. Then
$n_{f_1} = n_{f_2}$. Then  $f_1 = f_2$.
$f_1 = f_2$.
Proof. (i) On the one hand,
 \[ n_f = \overline{s\, r_k\, e_k\, \ldots\, r_2\, e_2\, r_1\, e_1}^{\boldsymbol{b}} \geqslant \overline{1\, \underbrace{0\, 0\, \ldots\, 0\, 0}_{2k\text{ zeros}}}^{\boldsymbol{b}} = \prod_{i=1}^k p(q^{2i-1}-1) > \prod_{i=1}^k q^{2i-1} = q^{k^2}. \]
\[ n_f = \overline{s\, r_k\, e_k\, \ldots\, r_2\, e_2\, r_1\, e_1}^{\boldsymbol{b}} \geqslant \overline{1\, \underbrace{0\, 0\, \ldots\, 0\, 0}_{2k\text{ zeros}}}^{\boldsymbol{b}} = \prod_{i=1}^k p(q^{2i-1}-1) > \prod_{i=1}^k q^{2i-1} = q^{k^2}. \]
On the other hand,
 \[ n_f = \overline{s\, r_k\, e_k\, \ldots\, r_2\, e_2\, r_1\, e_1}^{\boldsymbol{b}} \leqslant \overline{(q^{3k}+1)\, \underbrace{0\, 0\, \ldots\, 0\, 0}_{2k\text{ zeros}}}^{\boldsymbol{b}} = (q^{3k}+1) \prod_{i=1}^k p(q^{2i-1}-1) = q^{k^2+O(k)}, \]
\[ n_f = \overline{s\, r_k\, e_k\, \ldots\, r_2\, e_2\, r_1\, e_1}^{\boldsymbol{b}} \leqslant \overline{(q^{3k}+1)\, \underbrace{0\, 0\, \ldots\, 0\, 0}_{2k\text{ zeros}}}^{\boldsymbol{b}} = (q^{3k}+1) \prod_{i=1}^k p(q^{2i-1}-1) = q^{k^2+O(k)}, \]
as ![]() $p \leqslant q$. This shows that
$p \leqslant q$. This shows that ![]() $n_f = q^{k^2+O(k)}$.
$n_f = q^{k^2+O(k)}$.
(ii) Let ![]() $n = n_{f_1} = n_{f_2}$. Suppose that
$n = n_{f_1} = n_{f_2}$. Suppose that ![]() $f_1\in \mathcal {F}_{k_1}$ and
$f_1\in \mathcal {F}_{k_1}$ and ![]() $f_2\in \mathcal {F}_{k_2}$. By part (i), we have
$f_2\in \mathcal {F}_{k_2}$. By part (i), we have
from which we infer that ![]() ${k_1 = k_2+O(1)}$. Let
${k_1 = k_2+O(1)}$. Let ![]() $k = \min (k_1, k_2)$. Since
$k = \min (k_1, k_2)$. Since ![]() $n_{f_1} = n_{f_2} = n$, we also have
$n_{f_1} = n_{f_2} = n$, we also have
The left- and right-hand side are two base-![]() $\boldsymbol {b}$ representations of the same natural number, and since the
$\boldsymbol {b}$ representations of the same natural number, and since the ![]() $i$th digit is between
$i$th digit is between ![]() $0$ and
$0$ and ![]() $b_i-1$ in both cases, we see that
$b_i-1$ in both cases, we see that ![]() ${e_i(f_1) = e_i(f_2)}$ (and
${e_i(f_1) = e_i(f_2)}$ (and ![]() ${r_i(f_1) = r_i(f_2)}$) for all
${r_i(f_1) = r_i(f_2)}$) for all ![]() ${1\leqslant i\leqslant k}$. By the definition of
${1\leqslant i\leqslant k}$. By the definition of ![]() $e_i$, this implies that
$e_i$, this implies that ![]() ${f_1 \equiv f_2\pmod {g_i}}$. By the Chinese remainder theorem, we deduce that
${f_1 \equiv f_2\pmod {g_i}}$. By the Chinese remainder theorem, we deduce that
However, ![]() $\deg (f_1-f_2) \leqslant c k^2 + O(k)$ by definition of
$\deg (f_1-f_2) \leqslant c k^2 + O(k)$ by definition of ![]() $\mathcal {F}_k$, whereas
$\mathcal {F}_k$, whereas ![]() $\deg (g_1\cdots g_k) = k^2$. Therefore,
$\deg (g_1\cdots g_k) = k^2$. Therefore, ![]() $\deg (f_1-f_2) < \deg (g_1\cdots g_k)$ if
$\deg (f_1-f_2) < \deg (g_1\cdots g_k)$ if ![]() $C_0$ is sufficiently large, and (5) can only hold if
$C_0$ is sufficiently large, and (5) can only hold if ![]() $f_1 = f_2$.
$f_1 = f_2$.
4. Sidon property
Lemma 4.1 Let ![]() $f_1, f_2, f_3, f_4\in \mathcal {F}$ be such that
$f_1, f_2, f_3, f_4\in \mathcal {F}$ be such that ![]() $n_{f_1} + n_{f_2} = n_{f_3} + n_{f_4}$. Then
$n_{f_1} + n_{f_2} = n_{f_3} + n_{f_4}$. Then ![]() $\{f_1, f_2\} = \{f_3, f_4\}$.
$\{f_1, f_2\} = \{f_3, f_4\}$.
Proof. Without loss of generality, suppose that ![]() $f_i\in \mathcal {F}_{k_i}$ for
$f_i\in \mathcal {F}_{k_i}$ for ![]() $i\in \{1,2,3,4\}$, where
$i\in \{1,2,3,4\}$, where ![]() $k_1\geqslant k_2$ and
$k_1\geqslant k_2$ and ![]() ${k_3\geqslant k_4}$. By part (i) of Lemma 3.4, we have
${k_3\geqslant k_4}$. By part (i) of Lemma 3.4, we have ![]() $q^{k_1^2+O(k_1)} = n_{f_1} + n_{f_2} = n_{f_3} + n_{f_4} = q^{k_3^2 + O(k_3)}$ and, thus,
$q^{k_1^2+O(k_1)} = n_{f_1} + n_{f_2} = n_{f_3} + n_{f_4} = q^{k_3^2 + O(k_3)}$ and, thus, ![]() $k_1 = k_3 + O(1)$.
$k_1 = k_3 + O(1)$.
We claim that ![]() $k_2 = k_4 + O(1)$. Write the integer
$k_2 = k_4 + O(1)$. Write the integer ![]() $n := n_{f_1} + n_{f_2} = n_{f_3} + n_{f_4}$ in base
$n := n_{f_1} + n_{f_2} = n_{f_3} + n_{f_4}$ in base ![]() $\boldsymbol {b}$, as
$\boldsymbol {b}$, as
for some ![]() $0\leqslant x_i < q^{2i-1}-1$ and
$0\leqslant x_i < q^{2i-1}-1$ and ![]() $0\leqslant y_1 < p$, where
$0\leqslant y_1 < p$, where ![]() $x_l$ and
$x_l$ and ![]() $y_l$ are not both zero. Let us align the base-
$y_l$ are not both zero. Let us align the base-![]() $\boldsymbol {b}$ digits of
$\boldsymbol {b}$ digits of ![]() $n_{f_1}$,
$n_{f_1}$, ![]() $n_{f_2}$ and
$n_{f_2}$ and ![]() $n$:
$n$:

Since ![]() $n_{f_1} + n_{f_2} = n$ and
$n_{f_1} + n_{f_2} = n$ and ![]() $r_i(f_j) \leqslant p/2-1$ for all
$r_i(f_j) \leqslant p/2-1$ for all ![]() $i$ and
$i$ and ![]() $j$, we can easily express the digits
$j$, we can easily express the digits ![]() $x_i$ and
$x_i$ and ![]() $y_i$ in terms of the digits of
$y_i$ in terms of the digits of ![]() $n_{f_1}$ and
$n_{f_1}$ and ![]() $n_{f_2}$. The computation gets slightly more complicated when
$n_{f_2}$. The computation gets slightly more complicated when ![]() $i$ is close to
$i$ is close to ![]() $k_2$ (or larger than
$k_2$ (or larger than ![]() $k_1$) because
$k_1$) because ![]() $s(f_2)$ can be as large as
$s(f_2)$ can be as large as ![]() $q^{3k_2}$, which exceeds
$q^{3k_2}$, which exceeds ![]() $b_{2k_2+1} = q^{2k_2+1}-1$.
$b_{2k_2+1} = q^{2k_2+1}-1$.
On the one hand, for ![]() $1\leqslant i\leqslant k_2$, we have:
$1\leqslant i\leqslant k_2$, we have:
•
 $x_i = \big [e_i(f_1) + e_i(f_2) \ \mathrm {mod}\ q^{2i-1}-1 \big ]$; and
$x_i = \big [e_i(f_1) + e_i(f_2) \ \mathrm {mod}\ q^{2i-1}-1 \big ]$; and•
 $y_i = r_i(f_1) + r_i(f_2) + \mathbf {1}_{e_i(f_1) + e_i(f_2) \geqslant q^{2i-1}-1}$.
$y_i = r_i(f_1) + r_i(f_2) + \mathbf {1}_{e_i(f_1) + e_i(f_2) \geqslant q^{2i-1}-1}$.
On the other hand, for ![]() $k_2+3\leqslant i\leqslant k_1$ we have:Footnote 4
$k_2+3\leqslant i\leqslant k_1$ we have:Footnote 4
•
 $x_i = e_i(f_1)$; and
$x_i = e_i(f_1)$; and•
 $y_i = r_i(f_1)$.
$y_i = r_i(f_1)$.
In particular, for ![]() $1\leqslant i\leqslant k_2$ we have
$1\leqslant i\leqslant k_2$ we have ![]() $y_i \in A+A+\{0, 1\}$, whereas for
$y_i \in A+A+\{0, 1\}$, whereas for ![]() $k_2+3 \leqslant i\leqslant k_1$ we have
$k_2+3 \leqslant i\leqslant k_1$ we have ![]() $y_i\in A$. Let
$y_i\in A$. Let ![]() $i_0$ be the largest integer
$i_0$ be the largest integer ![]() $\leqslant l$ such that
$\leqslant l$ such that ![]() $y_1, \ldots, y_{i_0} \in A+A+\{0, 1\}$. If
$y_1, \ldots, y_{i_0} \in A+A+\{0, 1\}$. If ![]() $k_2+3>k_1$, then
$k_2+3>k_1$, then ![]() $i_0 = k_1+O(1) = k_2 + O(1)$. Otherwise, since
$i_0 = k_1+O(1) = k_2 + O(1)$. Otherwise, since ![]() $A$ and
$A$ and ![]() $A+A+\{0, 1\}$ are disjoint by Lemma 3.1(i), we have
$A+A+\{0, 1\}$ are disjoint by Lemma 3.1(i), we have ![]() $k_2 \leqslant i_0 < k_2+3$. Hence,
$k_2 \leqslant i_0 < k_2+3$. Hence, ![]() $i_0 = k_2 + O(1)$ in both cases.
$i_0 = k_2 + O(1)$ in both cases.
Repeating the whole argument with ![]() $f_3$ and
$f_3$ and ![]() $f_4$ in place of
$f_4$ in place of ![]() $f_1$ and
$f_1$ and ![]() $f_2$, we obtain that
$f_2$, we obtain that ![]() $i_0 = k_4 + O(1)$, whence
$i_0 = k_4 + O(1)$, whence ![]() $k_2 = k_4 + O(1)$ as claimed.
$k_2 = k_4 + O(1)$ as claimed.
Our previous computations have shown that
for ![]() $1\leqslant i \leqslant \min (k_2, k_4)$, and
$1\leqslant i \leqslant \min (k_2, k_4)$, and
for ![]() $\max (k_2, k_4)+3 \leqslant i\leqslant \min (k_1, k_3)$.
$\max (k_2, k_4)+3 \leqslant i\leqslant \min (k_1, k_3)$.
By the definition of ![]() $e_i(f)$ and the Chinese remainder theorem, this implies that
$e_i(f)$ and the Chinese remainder theorem, this implies that
 \begin{equation} f_1f_2 \equiv f_3f_4 \biggl( \mathrm{mod}{\prod_{i=1}^{\min(k_2, k_4)} g_i}\biggr) \end{equation}
\begin{equation} f_1f_2 \equiv f_3f_4 \biggl( \mathrm{mod}{\prod_{i=1}^{\min(k_2, k_4)} g_i}\biggr) \end{equation}and
 \begin{equation} f_1 \equiv f_3 \biggl( \mathrm{mod}{\prod_{i = \max(k_2, k_4)+3}^{\min(k_1, k_3)} g_i}\biggr). \end{equation}
\begin{equation} f_1 \equiv f_3 \biggl( \mathrm{mod}{\prod_{i = \max(k_2, k_4)+3}^{\min(k_1, k_3)} g_i}\biggr). \end{equation} Suppose first that ![]() $f_1 = f_3$. Then
$f_1 = f_3$. Then ![]() $n_{f_2} = n - n_{f_1} = n - n_{f_3} = n_{f_4}$ and, hence,
$n_{f_2} = n - n_{f_1} = n - n_{f_3} = n_{f_4}$ and, hence, ![]() $f_2 = f_4$ by Lemma 3.4(ii), which is what we needed to prove.
$f_2 = f_4$ by Lemma 3.4(ii), which is what we needed to prove.
If ![]() $f_1f_2 = f_3f_4$, we immediately conclude that
$f_1f_2 = f_3f_4$, we immediately conclude that ![]() $\{f_1, f_2\} = \{f_3, f_4\}$, since all
$\{f_1, f_2\} = \{f_3, f_4\}$, since all ![]() $f_i$ are irreducible monic polynomials.
$f_i$ are irreducible monic polynomials.
Hence, we may suppose that ![]() $f_1 \neq f_3$ and
$f_1 \neq f_3$ and ![]() $f_1f_2 \neq f_3f_4$. By (7) we must have
$f_1f_2 \neq f_3f_4$. By (7) we must have
 \[ c k_1^2+O(k_1) \geqslant \deg(f_1-f_3) \geqslant \deg \bigg( \prod_{i = k_2+O(1)}^{k_1-O(1)} g_i \bigg) = k_1^2-k_2^2 - O(k_1). \]
\[ c k_1^2+O(k_1) \geqslant \deg(f_1-f_3) \geqslant \deg \bigg( \prod_{i = k_2+O(1)}^{k_1-O(1)} g_i \bigg) = k_1^2-k_2^2 - O(k_1). \]
Similarly, by (6), we have
 \[ c k_1^2 + c k_2^2 + O(k_1) \geqslant \deg(f_1f_2 - f_3f_4) \geqslant \deg \bigg( \prod_{i=1}^{k_2 - O(1)} g_i \bigg) = k_2^2 - O(k_2). \]
\[ c k_1^2 + c k_2^2 + O(k_1) \geqslant \deg(f_1f_2 - f_3f_4) \geqslant \deg \bigg( \prod_{i=1}^{k_2 - O(1)} g_i \bigg) = k_2^2 - O(k_2). \]
Therefore, we have
 \[ \begin{cases} k_1^2 - k_2^2 \leqslant c k_1^2 + O(k_1),\\ k_2^2 \leqslant c k_1^2 + c k_2^2 + O(k_1). \end{cases} \]
\[ \begin{cases} k_1^2 - k_2^2 \leqslant c k_1^2 + O(k_1),\\ k_2^2 \leqslant c k_1^2 + c k_2^2 + O(k_1). \end{cases} \]
Hence,
which is impossible since ![]() $1-c > {c}/({1-c})$, if
$1-c > {c}/({1-c})$, if ![]() $C_0$ is sufficiently large.
$C_0$ is sufficiently large.
5. Asymptotic basis of order 3
Lemma 5.1 Let ![]() $m \geqslant 3$ be an integer. We can write
$m \geqslant 3$ be an integer. We can write ![]() $m = \overline {z\, y_k\, x_k\, \ldots \, y_2\, x_2\, y_1\, x_1}^{\boldsymbol {b}}$, for some
$m = \overline {z\, y_k\, x_k\, \ldots \, y_2\, x_2\, y_1\, x_1}^{\boldsymbol {b}}$, for some ![]() $k\geqslant 0$ and some integers
$k\geqslant 0$ and some integers ![]() $x_i, y_i, z$ satisfying:
$x_i, y_i, z$ satisfying:
•
 $0\leqslant x_i < q^{2i-1}-1$ for all
$0\leqslant x_i < q^{2i-1}-1$ for all  $1\leqslant i\leqslant k$;
$1\leqslant i\leqslant k$;•
 $0\leqslant y_i < 2p$ for all
$0\leqslant y_i < 2p$ for all  $1\leqslant i\leqslant k$;
$1\leqslant i\leqslant k$;•
 $\{y_i-2, y_i-1, y_i\} \subset A+A+A$ for all
$\{y_i-2, y_i-1, y_i\} \subset A+A+A$ for all  $1\leqslant i\leqslant k$;
$1\leqslant i\leqslant k$;•
 $3\leqslant z \leqslant 6p q^{2k+1}$.
$3\leqslant z \leqslant 6p q^{2k+1}$.
Proof. We proceed in a similar way to the standard algorithm that generates the base-![]() $b$ expansion of an integer. Let us inductively define a sequence
$b$ expansion of an integer. Let us inductively define a sequence ![]() $(m_i)$ of integers
$(m_i)$ of integers ![]() $\geqslant 3$. Let
$\geqslant 3$. Let ![]() $m_1 := m$. Suppose we have defined
$m_1 := m$. Suppose we have defined ![]() $m_1, \ldots, m_{2l-1}$ for some
$m_1, \ldots, m_{2l-1}$ for some ![]() $l\geqslant 1$.
$l\geqslant 1$.
If ![]() $m_{2l-1} > 6p q^{2l-1}$, we define
$m_{2l-1} > 6p q^{2l-1}$, we define
and we set ![]() $m_{2l} := ({m_{2l-1} - x_l})/({q^{2l-1}-1})$.
$m_{2l} := ({m_{2l-1} - x_l})/({q^{2l-1}-1})$.
Let ![]() $0\leqslant y_l < 2p$ be an integer with
$0\leqslant y_l < 2p$ be an integer with ![]() ${y_l \equiv m_{2l} \pmod p}$ and such that
${y_l \equiv m_{2l} \pmod p}$ and such that
Such an integer exists by Lemma 3.1(ii) (note that ![]() $A+A+A \subset [0, 3p/2]$). We define
$A+A+A \subset [0, 3p/2]$). We define ![]() $m_{2l+1} := (m_{2l} - y_l)/{p}$. Since
$m_{2l+1} := (m_{2l} - y_l)/{p}$. Since ![]() $m_{2l-1} > 6p q^{2l-1}$, we have
$m_{2l-1} > 6p q^{2l-1}$, we have
We have thus constructed ![]() $x_l$,
$x_l$, ![]() $y_l$,
$y_l$, ![]() $m_{2l}$ and
$m_{2l}$ and ![]() $m_{2l+1}$.
$m_{2l+1}$.
Otherwise, if ![]() $m_{2l-1} \leqslant 6p q^{2l-1}$, so we can define
$m_{2l-1} \leqslant 6p q^{2l-1}$, so we can define ![]() $z := m_{2l-1}$ and stop the construction (thus,
$z := m_{2l-1}$ and stop the construction (thus, ![]() $k=l-1$).
$k=l-1$).
The procedure must stop since ![]() $(m_i)$ is decreasing. When the procedure terminates, we end up with integers
$(m_i)$ is decreasing. When the procedure terminates, we end up with integers ![]() $x_1, \ldots, x_k$,
$x_1, \ldots, x_k$, ![]() $y_1, \ldots, y_k$ and
$y_1, \ldots, y_k$ and ![]() $z$ that satisfy the required properties, by construction.
$z$ that satisfy the required properties, by construction.
Lemma 5.2 Let ![]() $d\geqslant 1$ and let
$d\geqslant 1$ and let ![]() $g\in \mathbb {F}_q[t]$ be a squarefree monic polynomial of degree
$g\in \mathbb {F}_q[t]$ be a squarefree monic polynomial of degree
for some ![]() $0 < \theta < 1$. Let
$0 < \theta < 1$. Let ![]() $a \in (\mathbb {F}_q[t]/(g))^{\times }$. Then, with
$a \in (\mathbb {F}_q[t]/(g))^{\times }$. Then, with ![]() $\phi (g) := \big |(\mathbb {F}_q[t]/(g))^{\times }\big |$, we have
$\phi (g) := \big |(\mathbb {F}_q[t]/(g))^{\times }\big |$, we have
 \[ \biggl| \sum_{\substack{f_1, f_2, f_3 \in \mathcal{P}_{d}\\ f_i~\mathrm{distinct}\\ f_1f_2f_3 \equiv a\ (\mathrm{mod}(g))}} \hspace{-0.3cm} 1 - \frac{1}{\phi(g)} { \big|\mathcal{P}_{d}\big|\choose 3} \biggr| \ll e^{O_{\theta}(d)} q^{({3d - \deg(g)})/{2}}. \]
\[ \biggl| \sum_{\substack{f_1, f_2, f_3 \in \mathcal{P}_{d}\\ f_i~\mathrm{distinct}\\ f_1f_2f_3 \equiv a\ (\mathrm{mod}(g))}} \hspace{-0.3cm} 1 - \frac{1}{\phi(g)} { \big|\mathcal{P}_{d}\big|\choose 3} \biggr| \ll e^{O_{\theta}(d)} q^{({3d - \deg(g)})/{2}}. \]
Proof. We use [Reference SawinSaw21, Lemma 9.14] with ![]() $\omega = 3$,
$\omega = 3$, ![]() $n_1 = n_2 = n_3 = d$,
$n_1 = n_2 = n_3 = d$, ![]() $n = 3d$ and
$n = 3d$ and ![]() $h = 1$ (meaning that
$h = 1$ (meaning that ![]() $c=0$). The author writes
$c=0$). The author writes ![]() $\mathbb {F}_q[t]^{+}$ and
$\mathbb {F}_q[t]^{+}$ and ![]() $\mathcal {M}_n$ for the set of monic polynomials in
$\mathcal {M}_n$ for the set of monic polynomials in ![]() $\mathbb {F}_q[t]$ and the set of monic polynomials of degree
$\mathbb {F}_q[t]$ and the set of monic polynomials of degree ![]() $n$ in
$n$ in ![]() $\mathbb {F}_q[t]$, respectively. The definition of
$\mathbb {F}_q[t]$, respectively. The definition of ![]() $H^{h}_{n_1, \ldots, n_{\omega }}(f)$ can be found at the bottom of [Reference SawinSaw21, p. 89]. In particular,
$H^{h}_{n_1, \ldots, n_{\omega }}(f)$ can be found at the bottom of [Reference SawinSaw21, p. 89]. In particular,
 \[ H^{1}_{d, d, d}(f) = d^3 \sum_{\substack{f_1, f_2, f_3 \in \mathcal{P}_{d}\\ f_i \text{ distinct}\\ f_1f_2f_3 = f}} 1, \]
\[ H^{1}_{d, d, d}(f) = d^3 \sum_{\substack{f_1, f_2, f_3 \in \mathcal{P}_{d}\\ f_i \text{ distinct}\\ f_1f_2f_3 = f}} 1, \]
and, thus,
 \[ \sum_{f\in \mathcal{M}_{3d}}H^{1}_{d, d, d}(f) = d^3 { \big|\mathcal{P}_{d}\big|\choose 3}. \]
\[ \sum_{f\in \mathcal{M}_{3d}}H^{1}_{d, d, d}(f) = d^3 { \big|\mathcal{P}_{d}\big|\choose 3}. \]
Since ![]() $c = 0$, the conclusion of [Reference SawinSaw21, Lemma 9.14] simplifies to
$c = 0$, the conclusion of [Reference SawinSaw21, Lemma 9.14] simplifies to
 \[ d^3 \biggl| \sum_{\substack{f_1, f_2, f_3 \in \mathcal{P}_{d}\\ f_i \text{ distinct}\\ f_1f_2f_3 \equiv a (\mathrm{mod}(g))}} \hspace{-0.3cm} 1 - \frac{1}{\phi(g)} { \big|\mathcal{P}_{d}\big|\choose 3} \biggr| \ll \frac{(3d)!}{(d!)^3} (O_{\theta} (q))^{({3d - \deg(g)})/{2}}. \]
\[ d^3 \biggl| \sum_{\substack{f_1, f_2, f_3 \in \mathcal{P}_{d}\\ f_i \text{ distinct}\\ f_1f_2f_3 \equiv a (\mathrm{mod}(g))}} \hspace{-0.3cm} 1 - \frac{1}{\phi(g)} { \big|\mathcal{P}_{d}\big|\choose 3} \biggr| \ll \frac{(3d)!}{(d!)^3} (O_{\theta} (q))^{({3d - \deg(g)})/{2}}. \]
By Stirling's formula, ![]() ${(3d)!}/{(d!)^3} \ll e^{O(d)}$, and we obtain Lemma 5.2.
${(3d)!}/{(d!)^3} \ll e^{O(d)}$, and we obtain Lemma 5.2.
Lemma 5.3 Let ![]() $m\geqslant q^{(C_0+2)^2}$. Then
$m\geqslant q^{(C_0+2)^2}$. Then ![]() $\mathbb {P}\big (m\not \in S+S+S\big ) \leqslant \exp (-m^{3c-1 - o(1)})$ as
$\mathbb {P}\big (m\not \in S+S+S\big ) \leqslant \exp (-m^{3c-1 - o(1)})$ as ![]() $m\to +\infty$.Footnote 5
$m\to +\infty$.Footnote 5
Proof. Let ![]() $m \geqslant q^{(C_0+2)^2}$. We write
$m \geqslant q^{(C_0+2)^2}$. We write ![]() $m = \overline {z\, y_k\, x_k\, \ldots \, y_2\, x_2\, y_1\, x_1}^{\boldsymbol {b}}$ with
$m = \overline {z\, y_k\, x_k\, \ldots \, y_2\, x_2\, y_1\, x_1}^{\boldsymbol {b}}$ with ![]() $x_i$,
$x_i$, ![]() $y_i$ and z satisfying the conclusion of Lemma 5.1. By a computation similar to that in Lemma 3.4(i), we have
$y_i$ and z satisfying the conclusion of Lemma 5.1. By a computation similar to that in Lemma 3.4(i), we have
In particular, ![]() $k \geqslant C_0$ and
$k \geqslant C_0$ and ![]() $m = q^{k^2+O(k)}$.
$m = q^{k^2+O(k)}$.
We show that ![]() $m$ is very likely to be expressible as
$m$ is very likely to be expressible as ![]() $n_{f_1}+n_{f_2}+n_{f_3}$ for some
$n_{f_1}+n_{f_2}+n_{f_3}$ for some ![]() $f_i\in \mathcal {F}_k$.
$f_i\in \mathcal {F}_k$.
We first focus on the digits ![]() $x_i$. By the Chinese remainder theorem, there is some
$x_i$. By the Chinese remainder theorem, there is some ![]() $a\in \mathbb {F}_q[t]$ such that
$a\in \mathbb {F}_q[t]$ such that
for all ![]() $1\leqslant i\leqslant k$. Let
$1\leqslant i\leqslant k$. Let ![]() $g = \prod _{1\leqslant i\leqslant k} g_i$; it is a squarefree polynomial of degree
$g = \prod _{1\leqslant i\leqslant k} g_i$; it is a squarefree polynomial of degree ![]() $\deg (g) = k^2$. Let
$\deg (g) = k^2$. Let ![]() $d$ be an even integer with
$d$ be an even integer with ![]() $c k^2 \leqslant d < c(k+1)^2$. Let
$c k^2 \leqslant d < c(k+1)^2$. Let ![]() $\mathcal {E}$ be the set of all triples
$\mathcal {E}$ be the set of all triples ![]() $(f_1, f_2, f_3) \in (\mathcal {P}_{d})^3$ of distinct polynomials such that
$(f_1, f_2, f_3) \in (\mathcal {P}_{d})^3$ of distinct polynomials such that ![]() $f_1f_2f_3 \equiv a \pmod {g}$. By Lemma 5.2 with
$f_1f_2f_3 \equiv a \pmod {g}$. By Lemma 5.2 with ![]() $\theta = k^2/(3d) \leqslant 1/(3c) < 1$, we have
$\theta = k^2/(3d) \leqslant 1/(3c) < 1$, we have
Using the fact that ![]() $\phi (g) = \prod _{i=1}^k (q^{2i-1}-1) = q^{k^2-O(k)}$ and the bound (3) on the size of
$\phi (g) = \prod _{i=1}^k (q^{2i-1}-1) = q^{k^2-O(k)}$ and the bound (3) on the size of ![]() $\mathcal {P}_{d}$, we can simplify (8) to get
$\mathcal {P}_{d}$, we can simplify (8) to get
using ![]() $d = c k^2 + O(k)$ for the last step. If
$d = c k^2 + O(k)$ for the last step. If ![]() $C_0$ is sufficiently large, the error term is negligible and we obtain
$C_0$ is sufficiently large, the error term is negligible and we obtain
Let us estimate, for a fixed triple ![]() $(f_1, f_2, f_3)\in \mathcal {E}$, the probability that
$(f_1, f_2, f_3)\in \mathcal {E}$, the probability that ![]() $n_{f_1}+n_{f_2}+n_{f_3} = m$. By the definition of
$n_{f_1}+n_{f_2}+n_{f_3} = m$. By the definition of ![]() $n_{f_i}$, we can write
$n_{f_i}$, we can write
where ![]() $e_i'$,
$e_i'$, ![]() $r_i'$ and
$r_i'$ and ![]() $s'$ are defined by:
$s'$ are defined by:
•
 $e_i' = \big [e_i(f_1) + e_i(f_2) + e_i(f_3) \ \mathrm {mod}\ q^{2i-1}-1 \big ]$ for
$e_i' = \big [e_i(f_1) + e_i(f_2) + e_i(f_3) \ \mathrm {mod}\ q^{2i-1}-1 \big ]$ for  $1\leqslant i\leqslant k$;
$1\leqslant i\leqslant k$;•
 $r_i' = r_i(f_1) + r_i(f_2) + r_i(f_3) + \kappa _i$ for
$r_i' = r_i(f_1) + r_i(f_2) + r_i(f_3) + \kappa _i$ for  $1\leqslant i\leqslant k$, with
$1\leqslant i\leqslant k$, with
 \[ \kappa_i := \lfloor \frac{e_i(f_1) + e_i(f_2) + e_i(f_3)}{q^{2i-1}-1} \rfloor \in \{0, 1, 2\}; \]
\[ \kappa_i := \lfloor \frac{e_i(f_1) + e_i(f_2) + e_i(f_3)}{q^{2i-1}-1} \rfloor \in \{0, 1, 2\}; \]
•
 $s' = s(f_1) + s(f_2) + s(f_3)$.
$s' = s(f_1) + s(f_2) + s(f_3)$.
The assumption that ![]() $(f_1, f_2, f_3)\in \mathcal {E}$ ensures that
$(f_1, f_2, f_3)\in \mathcal {E}$ ensures that ![]() $e_i' = x_i$ for all
$e_i' = x_i$ for all ![]() $1\leqslant i \leqslant k$. Indeed, both
$1\leqslant i \leqslant k$. Indeed, both ![]() $e_i'$ and
$e_i'$ and ![]() $x_i$ are between
$x_i$ are between ![]() $0$ and
$0$ and ![]() $q^{2i-1}-2$, and
$q^{2i-1}-2$, and
Hence,
where we used the independence of the family of all random variables ![]() $r_i(f_j)$ and
$r_i(f_j)$ and ![]() $s(f_j)$ in the last step.
$s(f_j)$ in the last step.
Recall that ![]() $s'$ is the sum of three independent random numbers chosen uniformly in
$s'$ is the sum of three independent random numbers chosen uniformly in ![]() $\{1, 2, \ldots, q^{3k}\}$, so
$\{1, 2, \ldots, q^{3k}\}$, so ![]() $s'$ can be equal to any integer in the set
$s'$ can be equal to any integer in the set ![]() $\{3, 4, \ldots, 3q^{3k}\}$, each of which occurs with probability at least
$\{3, 4, \ldots, 3q^{3k}\}$, each of which occurs with probability at least ![]() $q^{-9k}$. Since
$q^{-9k}$. Since ![]() $z$ is a fixed element of
$z$ is a fixed element of ![]() $\{3, 4, \ldots, 6p q^{2k+1}\}$ and
$\{3, 4, \ldots, 6p q^{2k+1}\}$ and ![]() $6p q^{2k+1} \leqslant 3q^{3k}$, we get
$6p q^{2k+1} \leqslant 3q^{3k}$, we get
Similarly, ![]() $r_i'$ is the sum of three elements of
$r_i'$ is the sum of three elements of ![]() $A$ chosen uniformly and independently at random, plus a fixed carry
$A$ chosen uniformly and independently at random, plus a fixed carry ![]() $\kappa _i \in \{0, 1, 2\}$. Since
$\kappa _i \in \{0, 1, 2\}$. Since ![]() $\{y_i-2, y_i-1, y_i\} \subset A+A+A$ by Lemma 5.1, there is at least one triple
$\{y_i-2, y_i-1, y_i\} \subset A+A+A$ by Lemma 5.1, there is at least one triple ![]() $(a_1, a_2, a_3)\in A^3$ such that
$(a_1, a_2, a_3)\in A^3$ such that ![]() $a_1+a_2+a_3+\kappa _i = y_i$. Thus, we see that
$a_1+a_2+a_3+\kappa _i = y_i$. Thus, we see that ![]() $\mathbb {P}\big (r_i' = y_i\big ) \geqslant |A|^{-3} \geqslant p^{-3}$. We have thus shown that
$\mathbb {P}\big (r_i' = y_i\big ) \geqslant |A|^{-3} \geqslant p^{-3}$. We have thus shown that
To conclude the argument, we wish to restrict to a large subset ![]() $\mathcal {E}_0$ of
$\mathcal {E}_0$ of ![]() $\mathcal {E}$ such that no polynomial appears in more than one triple of
$\mathcal {E}$ such that no polynomial appears in more than one triple of ![]() $\mathcal {E}_0$. Observe that, if two triples
$\mathcal {E}_0$. Observe that, if two triples ![]() $(f, f_1, f_2)$ and
$(f, f_1, f_2)$ and ![]() $(f, f_3, f_4)$ are both in
$(f, f_3, f_4)$ are both in ![]() $\mathcal {E}$, then
$\mathcal {E}$, then ![]() $\{f_1, f_2\} = \{f_3, f_4\}$. Indeed, two such triples satisfy
$\{f_1, f_2\} = \{f_3, f_4\}$. Indeed, two such triples satisfy ![]() $f_1f_2 \equiv f^{-1}a \equiv f_3f_4 \pmod {g}$, which implies that
$f_1f_2 \equiv f^{-1}a \equiv f_3f_4 \pmod {g}$, which implies that ![]() $f_1f_2 = f_3f_4$ in
$f_1f_2 = f_3f_4$ in ![]() $\mathbb {F}_q[t]$ since
$\mathbb {F}_q[t]$ since
and thus ![]() $\{f_1, f_2\} = \{f_3, f_4\}$. In addition, if
$\{f_1, f_2\} = \{f_3, f_4\}$. In addition, if ![]() $(f_1, f_2, f_3)\in \mathcal {E}$ then so does
$(f_1, f_2, f_3)\in \mathcal {E}$ then so does ![]() $(f_{\sigma (1)}, f_{\sigma (2)}, f_{\sigma (3)})$ for every permutation
$(f_{\sigma (1)}, f_{\sigma (2)}, f_{\sigma (3)})$ for every permutation ![]() $\sigma$. Therefore, any given polynomial
$\sigma$. Therefore, any given polynomial ![]() $f\in \mathcal {P}_{d}$ appears at most once in a triple of
$f\in \mathcal {P}_{d}$ appears at most once in a triple of ![]() $\mathcal {E}$, up to permutations. This shows that there is a suitable subset
$\mathcal {E}$, up to permutations. This shows that there is a suitable subset ![]() $\mathcal {E}_0$ with
$\mathcal {E}_0$ with ![]() $\big |\mathcal {E}_0\big | = \tfrac 16 \big |\mathcal {E}\big |$.
$\big |\mathcal {E}_0\big | = \tfrac 16 \big |\mathcal {E}\big |$.
Therefore,
 \begin{align*} \mathbb{P}\big(m\not\in S+S+S\big) &\leqslant \mathbb{P} \biggl(\bigcap_{(f_1, f_2, f_3)\in \mathcal{E}_0} \{n_{f_1}+n_{f_2}+n_{f_3} \neq m\} \biggr)\\ &= \prod_{(f_1, f_2, f_3)\in \mathcal{E}_0} \mathbb{P}\big(n_{f_1}+n_{f_2}+n_{f_3} \neq m\big) \leqslant \big(1-q^{-O(k)}\big)^{|\mathcal{E}_0|}, \end{align*}
\begin{align*} \mathbb{P}\big(m\not\in S+S+S\big) &\leqslant \mathbb{P} \biggl(\bigcap_{(f_1, f_2, f_3)\in \mathcal{E}_0} \{n_{f_1}+n_{f_2}+n_{f_3} \neq m\} \biggr)\\ &= \prod_{(f_1, f_2, f_3)\in \mathcal{E}_0} \mathbb{P}\big(n_{f_1}+n_{f_2}+n_{f_3} \neq m\big) \leqslant \big(1-q^{-O(k)}\big)^{|\mathcal{E}_0|}, \end{align*}
using the independence of the family of random variables ![]() $(n_{f_1}+n_{f_2}+n_{f_3})_{(f_1, f_2, f_3)\in \mathcal {E}_0}$. By (9) and the simple inequality
$(n_{f_1}+n_{f_2}+n_{f_3})_{(f_1, f_2, f_3)\in \mathcal {E}_0}$. By (9) and the simple inequality ![]() $1-x\leqslant \exp (-x)$, we get
$1-x\leqslant \exp (-x)$, we get
as ![]() $m = q^{k^2+O(k)}$.
$m = q^{k^2+O(k)}$.
Theorem 5.4 With probability ![]() $1$, the elements of
$1$, the elements of ![]() $S$ form a Sidon sequence and an asymptotic basis of order
$S$ form a Sidon sequence and an asymptotic basis of order ![]() $3$.
$3$.
Proof. By Lemma 4.1, ![]() $S$ always has the Sidon property. By Lemma 5.3,
$S$ always has the Sidon property. By Lemma 5.3,
for sufficiently large ![]() $m$, so
$m$, so
by the Borel–Cantelli lemma. We conclude that ![]() $S$ is almost surely an asymptotic basis of order
$S$ is almost surely an asymptotic basis of order ![]() $3$.
$3$.
Acknowledgements
I would like to thank my advisors, Ben Green and James Maynard, for their expert guidance and continuing encouragement. I am very grateful to Oliver Riordan for pointing out an error in the appendix of an earlier version of this paper, and for suggesting the method used here to fix it. The author is supported by the Oxford Mathematical Institute and a Saven European Scholarship.
Conflicts of Interest
None.
Appendix A. Auxiliary set
In this section, we use the notation ![]() $f*g$ for the additive convolution
$f*g$ for the additive convolution
 \[ f*g (n) = (f*g) (n) := \sum_{\substack{a, b\in {\mathbb{Z}}\\ a+b=n}} f(a)g(b). \]
\[ f*g (n) = (f*g) (n) := \sum_{\substack{a, b\in {\mathbb{Z}}\\ a+b=n}} f(a)g(b). \]
Proof of Lemma 3.1 Let ![]() $I = \{1, 2, \ldots, \lfloor p/2 \rfloor - 1\} \subset {\mathbb {Z}}$.
$I = \{1, 2, \ldots, \lfloor p/2 \rfloor - 1\} \subset {\mathbb {Z}}$.
Let ![]() $R$ be the random set obtained by selecting each element of
$R$ be the random set obtained by selecting each element of ![]() $I$, independently, with probability
$I$, independently, with probability ![]() $Kp^{-2/3}$, where
$Kp^{-2/3}$, where ![]() $K = \lceil \log p \rceil$. In particular,
$K = \lceil \log p \rceil$. In particular, ![]() $\mathbb {E}\big [\big |R\big |\big ] \asymp Kp^{1/3}$.
$\mathbb {E}\big [\big |R\big |\big ] \asymp Kp^{1/3}$.
Note that ![]() $R$ almost satisfies property (i) of Lemma 3.1, in the sense that
$R$ almost satisfies property (i) of Lemma 3.1, in the sense that
 \[ \mathbb{E} \big[\big|R\cap (R+R+\{0, 1\})\big| \big] \leqslant \sum_{\substack{a,b,c \in I\\ a-b-c \in \{0, 1\}}} \mathbb{P}\big(a,b,c\in R\big). \]
\[ \mathbb{E} \big[\big|R\cap (R+R+\{0, 1\})\big| \big] \leqslant \sum_{\substack{a,b,c \in I\\ a-b-c \in \{0, 1\}}} \mathbb{P}\big(a,b,c\in R\big). \]
The probability ![]() $\mathbb {P}\big (a,b,c\in R\big )$ is
$\mathbb {P}\big (a,b,c\in R\big )$ is ![]() $(Kp^{-2/3})^k$ where
$(Kp^{-2/3})^k$ where ![]() $k = |\{a,b,c\}|$. Therefore,
$k = |\{a,b,c\}|$. Therefore,
It will be useful to know the bound ![]() $\big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } \ll 1$, which holds with high probability. Indeed, if
$\big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } \ll 1$, which holds with high probability. Indeed, if ![]() $\mathbf {1}_{R}*\mathbf {1}_{R}(n) \geqslant 9$ for some
$\mathbf {1}_{R}*\mathbf {1}_{R}(n) \geqslant 9$ for some ![]() $n\in {\mathbb {N}}$, then
$n\in {\mathbb {N}}$, then ![]() $R$ contains elements
$R$ contains elements ![]() $a_1< a_2<\cdots < a_8$ such that
$a_1< a_2<\cdots < a_8$ such that ![]() $a_i+a_{9-i} = n$ for all
$a_i+a_{9-i} = n$ for all ![]() $i$ and, thus,
$i$ and, thus,
 \begin{equation} \mathbb{P}\big(\exists n, \ \mathbf{1}_{R}*\mathbf{1}_{R}(n) \geqslant 9\big) \leqslant \sum_{n=1}^{p} \sum_{\substack{a_1, \ldots, a_8\in I\\ a_i\text{ distinct}\\ a_i+a_{9-i} = n}} \mathbb{P}\big(\forall i,\, a_i\in R\big) \ll p^5 (Kp^{-2/3})^8 \ll K^8p^{-1/3} \ll K^{-1}. \end{equation}
\begin{equation} \mathbb{P}\big(\exists n, \ \mathbf{1}_{R}*\mathbf{1}_{R}(n) \geqslant 9\big) \leqslant \sum_{n=1}^{p} \sum_{\substack{a_1, \ldots, a_8\in I\\ a_i\text{ distinct}\\ a_i+a_{9-i} = n}} \mathbb{P}\big(\forall i,\, a_i\in R\big) \ll p^5 (Kp^{-2/3})^8 \ll K^8p^{-1/3} \ll K^{-1}. \end{equation} Similarly, if ![]() $\mathbf {1}_{R}*\mathbf {1}_{-R}(n) \geqslant 8$ for some
$\mathbf {1}_{R}*\mathbf {1}_{-R}(n) \geqslant 8$ for some ![]() $n\in {\mathbb {Z}}^{\neq 0}$, then
$n\in {\mathbb {Z}}^{\neq 0}$, then ![]() $R$ contains distinct elements
$R$ contains distinct elements ![]() $a_1,\ldots, a_8$ such that
$a_1,\ldots, a_8$ such that ![]() $a_{2i}-a_{2i-1} = {n}$ for
$a_{2i}-a_{2i-1} = {n}$ for ![]() $i\in \{1,2,3,4\}$, and as before we get
$i\in \{1,2,3,4\}$, and as before we get
We now turn to property (ii) of Lemma 3.1. Let ![]() $n$ be an integer with
$n$ be an integer with ![]() $p/5 \leqslant n \leqslant 7p/5$. We show that
$p/5 \leqslant n \leqslant 7p/5$. We show that ![]() $n$ can be written in relatively many ways as the sum of three distinct elements of
$n$ can be written in relatively many ways as the sum of three distinct elements of ![]() $R$, with high probability. Let
$R$, with high probability. Let ![]() $\mathcal {T}(n)$ be the collection of all sets
$\mathcal {T}(n)$ be the collection of all sets ![]() $\{a, b, c\}$ of three pairwise distinct elements of
$\{a, b, c\}$ of three pairwise distinct elements of ![]() $I$ such that
$I$ such that ![]() $a+b+c = n$. We show that
$a+b+c = n$. We show that
 \begin{equation} \mathbb{P}\biggl( \sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset R} \leqslant K^{2}\biggr) \ll e^{-K^2}. \end{equation}
\begin{equation} \mathbb{P}\biggl( \sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset R} \leqslant K^{2}\biggr) \ll e^{-K^2}. \end{equation}To bound the left-hand side, we use Janson's inequality. This inequality involves the quantities
 \[ \lambda := \mathbb{E} \biggl[ \sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset R} \biggr] = \sum_{\substack{T\in \mathcal{T}(n)}} (Kp^{-2/3})^3 \gg p^2(Kp^{-2/3})^3 = K^3 \]
\[ \lambda := \mathbb{E} \biggl[ \sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset R} \biggr] = \sum_{\substack{T\in \mathcal{T}(n)}} (Kp^{-2/3})^3 \gg p^2(Kp^{-2/3})^3 = K^3 \]
and
 \[ \Delta := \sum_{\substack{T_1, T_2\in \mathcal{T}(n)\\ T_1\cap T_2\neq \emptyset \\ T_1\neq T_2}} \mathbb{P}\big(T_1\cup T_2\subset R\big). \]
\[ \Delta := \sum_{\substack{T_1, T_2\in \mathcal{T}(n)\\ T_1\cap T_2\neq \emptyset \\ T_1\neq T_2}} \mathbb{P}\big(T_1\cup T_2\subset R\big). \]
Janson's inequality [Reference Janson, Rucinski and LuczakJRL11, Theorem 2.14] gives
 \begin{equation} \mathbb{P}\biggl( \sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset R} \leqslant \tfrac12 \lambda\biggr) \leqslant \exp \left( -\frac{\lambda^2}{8(\lambda+\Delta)}\right). \end{equation}
\begin{equation} \mathbb{P}\biggl( \sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset R} \leqslant \tfrac12 \lambda\biggr) \leqslant \exp \left( -\frac{\lambda^2}{8(\lambda+\Delta)}\right). \end{equation} Observe that, if ![]() $T_1, T_2\in \mathcal {T}(n)$ are distinct but not disjoint, we must have
$T_1, T_2\in \mathcal {T}(n)$ are distinct but not disjoint, we must have ![]() $\big |T_1 \cap T_2\big | = 1$, so there are pairwise distinct elements
$\big |T_1 \cap T_2\big | = 1$, so there are pairwise distinct elements ![]() $a, b_1, b_2, c_1, c_2\in I$ such that
$a, b_1, b_2, c_1, c_2\in I$ such that ![]() $T_1 = \{a, b_1, c_1\}$ and
$T_1 = \{a, b_1, c_1\}$ and ![]() $T_2 = \{a, b_2, c_2\}$. In particular,
$T_2 = \{a, b_2, c_2\}$. In particular,
and there are ![]() $\ll p^3$ such pairs
$\ll p^3$ such pairs ![]() $(T_1, T_2)$. Hence,
$(T_1, T_2)$. Hence,
Provided ![]() $p$ is larger than some absolute constant, we have
$p$ is larger than some absolute constant, we have ![]() $K^{2} \leqslant \tfrac 12 \lambda$, so (A.4) follows from (A.5), using our estimates for
$K^{2} \leqslant \tfrac 12 \lambda$, so (A.4) follows from (A.5), using our estimates for ![]() $\lambda$ and
$\lambda$ and ![]() $\Delta$. By the union bound, we get
$\Delta$. By the union bound, we get
 \begin{align} \mathbb{P} \biggl(
\exists n\in [p/5, 7p/5]\cap {\mathbb{Z}},\
\sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset
R} \leqslant K^{2} \biggr) \ll p e^{-K^2} \ll K^{-1}.
\end{align}
\begin{align} \mathbb{P} \biggl(
\exists n\in [p/5, 7p/5]\cap {\mathbb{Z}},\
\sum_{\substack{T\in \mathcal{T}(n)}} \mathbf{1}_{T\subset
R} \leqslant K^{2} \biggr) \ll p e^{-K^2} \ll K^{-1}.
\end{align} We have shown that, typically, ![]() $R$ satisfies property (ii) of Lemma 3.1 in a robust sense (by (A.6)), but
$R$ satisfies property (ii) of Lemma 3.1 in a robust sense (by (A.6)), but ![]() $R$ just fails to satisfy property (i) (see (A.1)).
$R$ just fails to satisfy property (i) (see (A.1)).
We define ![]() $X := R\cap (R+R+\{0, 1\})$ and
$X := R\cap (R+R+\{0, 1\})$ and ![]() $A := R\setminus X$. This set
$A := R\setminus X$. This set ![]() $A$ satisfies property (i) of Lemma 3.1 by construction. We must show that
$A$ satisfies property (i) of Lemma 3.1 by construction. We must show that ![]() $A$ still satisfies property (ii) of Lemma 3.1, with high probability.
$A$ still satisfies property (ii) of Lemma 3.1, with high probability.
Let ![]() $n\in [p/5, 7p/5]\cap {\mathbb {Z}}$. We know that, with high probability,
$n\in [p/5, 7p/5]\cap {\mathbb {Z}}$. We know that, with high probability, ![]() $n$ is the sum of three distinct elements of
$n$ is the sum of three distinct elements of ![]() $R$ in many different ways. Thus, having
$R$ in many different ways. Thus, having ![]() $n\not \in A+A+A$ means that, whenever
$n\not \in A+A+A$ means that, whenever ![]() $n$ is written as
$n$ is written as ![]() $n = a+b+c$ with distinct
$n = a+b+c$ with distinct ![]() $a,b,c\in R$, at least one of
$a,b,c\in R$, at least one of ![]() $a,b,c$ is in
$a,b,c$ is in ![]() $X$.
$X$.
Define
Suppose that ![]() $n$ is such that
$n$ is such that
We claim that either ![]() $\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{R}(m) \geqslant 10$,
$\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{R}(m) \geqslant 10$, ![]() $\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) \geqslant 10$, or there are four tuples
$\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) \geqslant 10$, or there are four tuples ![]() $(a_i, b_i, c_i, d_i, e_i)_{1\leqslant i \leqslant 4} \in \mathcal {Q}(n) \cap R^5$ such that, for all
$(a_i, b_i, c_i, d_i, e_i)_{1\leqslant i \leqslant 4} \in \mathcal {Q}(n) \cap R^5$ such that, for all ![]() $1\leqslant i< j\leqslant 4$,
$1\leqslant i< j\leqslant 4$,
Suppose first that there is some ![]() $a\in R$ appearing as the first coordinate of
$a\in R$ appearing as the first coordinate of ![]() $200$ tuples
$200$ tuples
Then ![]() $n-a$ can be written as
$n-a$ can be written as ![]() $b_i+c_i$ for all
$b_i+c_i$ for all ![]() $1\leqslant i\leqslant 200$. If
$1\leqslant i\leqslant 200$. If ![]() $\mathbf {1}_{R} *\mathbf {1}_{R}(n-a) < 10$, there are
$\mathbf {1}_{R} *\mathbf {1}_{R}(n-a) < 10$, there are ![]() $b,c\in R$ such that
$b,c\in R$ such that ![]() $b_i = b$ and
$b_i = b$ and ![]() $c_i = c$ for at least
$c_i = c$ for at least ![]() $20$ values of
$20$ values of ![]() $i\in \{1, \ldots, 200\}$, say for
$i\in \{1, \ldots, 200\}$, say for ![]() $i \in J$ where
$i \in J$ where ![]() $|J| \geqslant 20$. In turn, this implies that
$|J| \geqslant 20$. In turn, this implies that ![]() $d_i + e_i \in \{c-1, c\}$ for all
$d_i + e_i \in \{c-1, c\}$ for all ![]() $i\in J$, but if
$i\in J$, but if ![]() $\mathbf {1}_{R} *\mathbf {1}_{R}(c-1) < 10$ and
$\mathbf {1}_{R} *\mathbf {1}_{R}(c-1) < 10$ and ![]() $\mathbf {1}_{R} *\mathbf {1}_{R}(c) < 10$ there must exist two distinct indices
$\mathbf {1}_{R} *\mathbf {1}_{R}(c) < 10$ there must exist two distinct indices ![]() $i, j\in J$ such that
$i, j\in J$ such that ![]() $(d_i, e_i) = (d_j, e_j)$. This is impossible since
$(d_i, e_i) = (d_j, e_j)$. This is impossible since ![]() $(a, b_i, c_i, d_i, e_i)$ and
$(a, b_i, c_i, d_i, e_i)$ and ![]() $(a, b_j, c_j, d_j, e_j)$ are distinct tuples.
$(a, b_j, c_j, d_j, e_j)$ are distinct tuples.
Similar reasoning shows that no ![]() $r\in R$ can appear as the second or third coordinate of
$r\in R$ can appear as the second or third coordinate of ![]() $200$ tuples in
$200$ tuples in ![]() $\mathcal {Q}(n) \cap R^5$, unless
$\mathcal {Q}(n) \cap R^5$, unless ![]() $\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{R}(m) \geqslant 10$.
$\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{R}(m) \geqslant 10$.
Suppose that there is some ![]() $d\in R$ that appears as the fourth coordinate of
$d\in R$ that appears as the fourth coordinate of ![]() $200$ tuples
$200$ tuples
Then ![]() $c_i-e_i \in \{d, d+1\}$ for all
$c_i-e_i \in \{d, d+1\}$ for all ![]() $i$. If
$i$. If ![]() $\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) < 10$, there are
$\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) < 10$, there are ![]() $c, e\in R$ and at least
$c, e\in R$ and at least ![]() $10$ values of
$10$ values of ![]() $i$ such that
$i$ such that ![]() $c_i = c$ and
$c_i = c$ and ![]() $e_i = e$. Thus, for these
$e_i = e$. Thus, for these ![]() $\geqslant 10$ values of
$\geqslant 10$ values of ![]() $i$, we have
$i$, we have ![]() $a_i + b_i = n-c$. If
$a_i + b_i = n-c$. If ![]() $\mathbf {1}_{R} *\mathbf {1}_{R}(n-c) < 10$, there are two distinct indices
$\mathbf {1}_{R} *\mathbf {1}_{R}(n-c) < 10$, there are two distinct indices ![]() $i,j$ such that
$i,j$ such that ![]() $(a_i, b_i, c_i, d, e_i) = (a_j, b_j, c_j, d, e_j)$, a contradiction.
$(a_i, b_i, c_i, d, e_i) = (a_j, b_j, c_j, d, e_j)$, a contradiction.
The same reasoning shows that no ![]() $e\in R$ appears in
$e\in R$ appears in ![]() $200$ distinct elements of
$200$ distinct elements of ![]() $\mathcal {Q}(n) \cap R^5$, unless
$\mathcal {Q}(n) \cap R^5$, unless ![]() $\big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } \geqslant 10$ or
$\big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } \geqslant 10$ or ![]() $\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) \geqslant 10$.
$\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) \geqslant 10$.
The claim follows easily from these observations. Indeed, suppose that ![]() $\big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } < 10$,
$\big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } < 10$, ![]() $\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) < 10$ and
$\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) < 10$ and ![]() $\big |\mathcal {Q}(n) \cap R^5\big |\geqslant K$. Let
$\big |\mathcal {Q}(n) \cap R^5\big |\geqslant K$. Let ![]() $(a_1, b_1, c_1, d_1, e_1)$ be an arbitrary element of
$(a_1, b_1, c_1, d_1, e_1)$ be an arbitrary element of ![]() $\mathcal {Q}(n) \cap R^5$. The previous observations show that the number of tuples in
$\mathcal {Q}(n) \cap R^5$. The previous observations show that the number of tuples in ![]() $\mathcal {Q}(n) \cap R^5$ having a coordinate in
$\mathcal {Q}(n) \cap R^5$ having a coordinate in ![]() $\{a_1, \ldots, e_1\}$ is bounded above by an absolute constant. Since
$\{a_1, \ldots, e_1\}$ is bounded above by an absolute constant. Since ![]() $K$ is assumed to be sufficiently large, we can find another tuple
$K$ is assumed to be sufficiently large, we can find another tuple ![]() $(a_2, b_2, c_2, d_2, e_2)$ such that
$(a_2, b_2, c_2, d_2, e_2)$ such that ![]() $\{a_1, \ldots, e_1\} \cap \{a_2, \ldots, e_2\} = \emptyset$. Repeating, we find four tuples
$\{a_1, \ldots, e_1\} \cap \{a_2, \ldots, e_2\} = \emptyset$. Repeating, we find four tuples ![]() $(a_i, b_i, c_i, d_i, e_i)_{1\leqslant i\leqslant 4}\in \mathcal {Q}(n) \cap R^5$ satisfying (A.7).
$(a_i, b_i, c_i, d_i, e_i)_{1\leqslant i\leqslant 4}\in \mathcal {Q}(n) \cap R^5$ satisfying (A.7).
By this claim and the union bound, we deduce that
 \begin{align*} &\mathbb{P} \bigl(\exists
n\in [p/5, 7p/5]\cap {\mathbb{Z}},
\big|\mathcal{Q}(n) \cap R^5\big|\geqslant K\bigr)\\
&\quad \leqslant \mathbb{P}\bigl( \big\|\mathbf{1}_{R}
*\mathbf{1}_{R}\big\|_{\infty} \geqslant 10\bigr) +
\mathbb{P} \bigl(\max_{m\in {\mathbb{N}}}
\mathbf{1}_{R} *\mathbf{1}_{-R}(m) \geqslant 10\bigr) \\ &\qquad\quad +
\sum_{n\in [p/5, 7p/5]\cap {\mathbb{Z}}}\
\sum_{\substack{(a_i, b_i, c_i, d_i, e_i)_{1\leqslant
i\leqslant 4} \in \mathcal{Q}(n) \\ \text{satisfying
(A.7)}}} \mathbb{P} \bigl(\forall i,\ a_i, b_i,
c_i, d_i, e_i\in R \bigr). \end{align*}
\begin{align*} &\mathbb{P} \bigl(\exists
n\in [p/5, 7p/5]\cap {\mathbb{Z}},
\big|\mathcal{Q}(n) \cap R^5\big|\geqslant K\bigr)\\
&\quad \leqslant \mathbb{P}\bigl( \big\|\mathbf{1}_{R}
*\mathbf{1}_{R}\big\|_{\infty} \geqslant 10\bigr) +
\mathbb{P} \bigl(\max_{m\in {\mathbb{N}}}
\mathbf{1}_{R} *\mathbf{1}_{-R}(m) \geqslant 10\bigr) \\ &\qquad\quad +
\sum_{n\in [p/5, 7p/5]\cap {\mathbb{Z}}}\
\sum_{\substack{(a_i, b_i, c_i, d_i, e_i)_{1\leqslant
i\leqslant 4} \in \mathcal{Q}(n) \\ \text{satisfying
(A.7)}}} \mathbb{P} \bigl(\forall i,\ a_i, b_i,
c_i, d_i, e_i\in R \bigr). \end{align*}
By (A.2) and (A.3), the probabilities ![]() $\mathbb {P}\big( \big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } \geqslant 10\big)$ and
$\mathbb {P}\big( \big \|\mathbf {1}_{R} *\mathbf {1}_{R}\big \|_{\infty } \geqslant 10\big)$ and ![]() $\mathbb {P} (\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) \geqslant 10)$ are
$\mathbb {P} (\max _{m\in {\mathbb {N}}} \mathbf {1}_{R} *\mathbf {1}_{-R}(m) \geqslant 10)$ are ![]() $\ll K^{-1}$. By (A.7), the events
$\ll K^{-1}$. By (A.7), the events ![]() $\{a_i, \ldots, e_i\in R\}$ and
$\{a_i, \ldots, e_i\in R\}$ and ![]() $\{a_j, \ldots, e_j\in R\}$ are independent for
$\{a_j, \ldots, e_j\in R\}$ are independent for ![]() $i\neq j$. Thus, the last probability is
$i\neq j$. Thus, the last probability is
 \[ \mathbb{P} (\forall i,\ a_i, b_i, c_i, d_i, e_i\in R) = \prod_{i=1}^4 \mathbb{P}\big(a_i, b_i, c_i, d_i, e_i\in R\big) = \prod_{i=1}^4 (Kp^{-2/3})^{|\{a_i, \ldots, e_i\}|}. \]
\[ \mathbb{P} (\forall i,\ a_i, b_i, c_i, d_i, e_i\in R) = \prod_{i=1}^4 \mathbb{P}\big(a_i, b_i, c_i, d_i, e_i\in R\big) = \prod_{i=1}^4 (Kp^{-2/3})^{|\{a_i, \ldots, e_i\}|}. \]
For ![]() $k\in \{3,4,5\}$, let
$k\in \{3,4,5\}$, let
It is not hard to see that ![]() $\big |\mathcal {Q}_k(n)\big | \ll p^{k-2}$ for
$\big |\mathcal {Q}_k(n)\big | \ll p^{k-2}$ for ![]() $k\in \{3,4,5\}$. Hence, we obtain
$k\in \{3,4,5\}$. Hence, we obtain
 \begin{align*} \mathbb{P} \bigl(\exists n\in [p/5, 7p/5]\cap {\mathbb{Z}},\ \big|\mathcal{Q}(n) \cap R^5\big|\geqslant K\bigr) &\ll K^{-1} + \sum_{n\in [p/5, 7p/5]\cap {\mathbb{Z}}} \prod_{i=1}^4 \sum_{k =3}^5 \big|\mathcal{Q}_{k}(n)\big| (Kp^{-2/3})^{k}\\ &\ll K^{-1} + p \biggl( \sum_{k=3}^5 p^{k-2} (Kp^{-2/3})^k \biggr)^4 \\ &\ll K^{-1} + p (K^{5} p^{-1/3})^4 \\ &\ll K^{-1}. \end{align*}
\begin{align*} \mathbb{P} \bigl(\exists n\in [p/5, 7p/5]\cap {\mathbb{Z}},\ \big|\mathcal{Q}(n) \cap R^5\big|\geqslant K\bigr) &\ll K^{-1} + \sum_{n\in [p/5, 7p/5]\cap {\mathbb{Z}}} \prod_{i=1}^4 \sum_{k =3}^5 \big|\mathcal{Q}_{k}(n)\big| (Kp^{-2/3})^{k}\\ &\ll K^{-1} + p \biggl( \sum_{k=3}^5 p^{k-2} (Kp^{-2/3})^k \biggr)^4 \\ &\ll K^{-1} + p (K^{5} p^{-1/3})^4 \\ &\ll K^{-1}. \end{align*}
The last computation and (A.6) imply that there is a set ![]() $R\subset I$ such that:
$R\subset I$ such that:
(a) for all
 $n\in [p/5, 7p/5]\cap {\mathbb {Z}}$, there are
$n\in [p/5, 7p/5]\cap {\mathbb {Z}}$, there are  $>K^2$ sets
$>K^2$ sets  $\{a,b,c\}$ of three distinct elements of
$\{a,b,c\}$ of three distinct elements of  $R$ such that
$R$ such that  $n = a+b+c$;
$n = a+b+c$;(b) for all
 $n\in [p/5, 7p/5]\cap {\mathbb {Z}}$, there are
$n\in [p/5, 7p/5]\cap {\mathbb {Z}}$, there are  $\ll K$ sets
$\ll K$ sets  $\{a,b,c\}$ of three distinct elements of
$\{a,b,c\}$ of three distinct elements of  $R$ such that
$R$ such that  $n = a+b+c$, with one of
$n = a+b+c$, with one of  $a,b,c$ in
$a,b,c$ in  $R+R+\{0, 1\}$;
$R+R+\{0, 1\}$;
since with high probability, both properties hold simultaneously.
As announced earlier, we define ![]() $X = R\cap (R+R+\{0, 1\}$ and
$X = R\cap (R+R+\{0, 1\}$ and ![]() $A = R\setminus X$. Then
$A = R\setminus X$. Then ![]() $A$ and
$A$ and ![]() $A+A+\{0, 1\}$ are disjoint by construction, and for every
$A+A+\{0, 1\}$ are disjoint by construction, and for every ![]() $n\in [p/5, 7p/5]\cap {\mathbb {Z}}$ there are
$n\in [p/5, 7p/5]\cap {\mathbb {Z}}$ there are ![]() $K^2 - O(K) \geqslant 1$ ways to write
$K^2 - O(K) \geqslant 1$ ways to write ![]() $n$ as the sum of three elements of
$n$ as the sum of three elements of ![]() $R$, none of which being in
$R$, none of which being in ![]() $X$. This means that we can write
$X$. This means that we can write ![]() $n$ as the sum of three elements of
$n$ as the sum of three elements of ![]() $A$, and we are done.
$A$, and we are done.