Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-25T20:48:25.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Slopes in eigenvarieties for definite unitary groups

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  22 November 2023

Lynnelle Ye
Lynnelle Ye*
Affiliation:
Stanford University, Building 380, Stanford, CA 94305, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize bounds of Liu–Wan–Xiao for slopes in eigencurves for definite unitary groups of rank 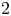$2$ to slopes in eigenvarieties for definite unitary groups of any rank. We show that for a definite unitary group of rank 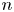$n$, the Newton polygon of the characteristic power series of the 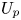$U_p$ Hecke operator has exact growth rate 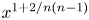$x^{1+2/{n(n-1)}}$, times a constant proportional to the distance of the weight from the boundary of weight space. The proof goes through the classification of forms associated to principal series representations. We also give a consequence for the geometry of these eigenvarieties over the boundary of weight space.

Keywords

eigenvarieties, p-adic automorphic forms

MSC classification

Primary: 11F85: $p$-adic theory, local fields
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F55: Other groups and their modular and automorphic forms (several variables)
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 1 , January 2024 , pp. 52 - 89
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was partially done with the support of a National Defense Science and Engineering Graduate Fellowship, and writing was completed with the support of a National Science Foundation Mathematical Sciences Postdoctoral Research Fellowship.

References

Andreatta, F., Iovita, A. and Pilloni, V., Le halo spectral, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 603–655.CrossRefGoogle Scholar
Baker, M., Conrad, B., Dasgupta, S., Teitelbaum, J. T. and Kedlaya, K. S., p-adic geometry: Lectures from the 2007 Arizona Winter School, University Lecture Series, vol. 45 (American Mathematical Society, 2008).Google Scholar
Bellaïche, J. and Chenevier, G., Families of Galois representations and Selmer groups, Astérisque 324 (2009), 1–314.Google Scholar
Birkbeck, C., Slopes of overconvergent Hilbert modular forms, Exp. Math. 30 (2021), 295–314.CrossRefGoogle Scholar
Borel, A., Some finiteness properties of adele groups over number fields, Publ. Math. Inst. Hautes Études Sci. 16 (1963), 5–30.CrossRefGoogle Scholar
Buzzard, K., On p-adic families of automorphic forms, in Modular curves and abelian varieties (Springer, 2004), 23–44.CrossRefGoogle Scholar
Buzzard, K., Eigenvarieties, L-functions and Galois representations, London Mathematical Society Lecture Note Series, vol. 320 (Cambridge University Press, 2007), 59–120.CrossRefGoogle Scholar
Buzzard, K. and Kilford, L. J. P., The $2$-adic eigencurve at the boundary of weight space, Compos. Math. 141 (2005), 605–619.CrossRefGoogle Scholar
Casselman, W., On some results of Atkin and Lehner, Math. Ann. 201 (1973), 301–314.CrossRefGoogle Scholar
Casselman, W., Introduction to admissible representations of $p$-adic groups, unpublished notes (1995).Google Scholar
Chenevier, G., Familles $p$-adiques de formes automorphes pour $GL_n$, J. Reine Angew. Math. 570 (2004), 143–217.Google Scholar
Coleman, R. and Mazur, B., The eigencurve, in Galois representations in arithmetic algebraic geometry, London Mathematical Society Lecture Note Series, vol. 254 (Cambridge University Press, 1998), 1–114.Google Scholar
Diao, H. and Yao, Z., The halo conjecture for GL2, Preprint (2023), arXiv:2302.07987.Google Scholar
Emerton, M., Jacquet modules of locally analytic representations of $p$-adic reductive groups I. Construction and first properties, Ann. Sci. Éc. Norm. Supér. (4) 39 (2006), 775–839.CrossRefGoogle Scholar
Emerton, M., On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms, Invent. Math. 164 (2006), 1–84.CrossRefGoogle Scholar
Fintzen, J., Types for tame $p$-adic groups, Ann. Math. 193 (2021), 303–346.CrossRefGoogle Scholar
Goodman, R. and Wallach, N. R., Symmetry, representations, and invariants, Graduate Texts in Mathematics, vol. 255 (Springer, 2009).CrossRefGoogle Scholar
Gross, B. H., Algebraic modular forms, Israel J. Math. 113 (1999), 61–93.CrossRefGoogle Scholar
Gulotta, D. R., Equidimensional adic eigenvarieties for groups with discrete series, Algebra Number Theory 13 (2019), 1907–1940.CrossRefGoogle Scholar
Hansen, D. and Newton, J., Universal eigenvarieties, trianguline Galois representations, and $p$-adic Langlands functoriality, J. Reine Angew. Math. 2017 (2017), 1–64.CrossRefGoogle Scholar
Howe, R. and Moy, A., Hecke algebra isomorphisms for $GL(n)$ over a $p$-adic field, J. Algebra 131 (1990), 388–424.CrossRefGoogle Scholar
Johansson, C. and Newton, J., Extended eigenvarieties for overconvergent cohomology, Algebra Number Theory 13 (2019), 93–158.CrossRefGoogle Scholar
Johansson, C. and Newton, J., Parallel weight 2 points on Hilbert modular eigenvarieties and the parity conjecture, Forum Math. Sigma 7 (2019), E27.CrossRefGoogle Scholar
Kilford, L. J. P., On the slopes of the $U_5$ operator acting on overconvergent modular forms, J. Théor. Nombres Bordeaux 20 (2008), 165–182; MR 2434162.CrossRefGoogle Scholar
Kilford, L. J. P. and McMurdy, K., Slopes of the $U_7$ operator acting on a space of overconvergent modular forms, LMS J. Comput. Math. 15 (2012), 113–139.CrossRefGoogle Scholar
Liu, R., Wan, D. and Xiao, L., The eigencurve over the boundary of weight space, Duke Math. J. 166 (2017), 1739–1787.CrossRefGoogle Scholar
Loeffler, D., Overconvergent algebraic automorphic forms, Proc. Lond. Math. Soc. 102 (2010), 193–228.CrossRefGoogle Scholar
Loeffler, D. and Weinstein, J., On the computation of local components of a newform, Math. Comput. 81 (2012), 1179–1200.CrossRefGoogle Scholar
Miller, E. and Sturmfels, B., Combinatorial commutative algebra, Graduate Texts in Mathematics, vol. 227 (Springer, 2004).Google Scholar
Newton, J. and Thorne, J. A., Symmetric power functoriality for holomorphic modular forms, Publ. Math. Inst. Hautes Études Sci. 134 (2021), 1–116.CrossRefGoogle Scholar
Ren, R. and Zhao, B., Spectral halo for Hilbert modular forms, Math. Ann. 382 (2022), 821–899.CrossRefGoogle Scholar
Roche, A., Types and Hecke algebras for principal series representations of split reductive $p$-adic groups, Ann. Sci. Éc. Norm. Supér. 31 (1998), 361–413.CrossRefGoogle Scholar
Roe, D., The 3-adic eigencurve at the boundary of weight space, Int. J. Number Theory 10 (2014), 1791–1806.CrossRefGoogle Scholar
Schneider, P., Teitelbaum, J. and an appendix by Prasad, D., $U(\mathfrak {g})$-finite locally analytic representations, Represent. Theory 5 (2001), 111–128.CrossRefGoogle Scholar
Serre, J.-P., Endomorphismes complètement continus des espaces de Banach $p$-adiques, Publ. Math. Inst. Hautes Études Sci. 12 (1962), 69–85.CrossRefGoogle Scholar
Wan, D., Dimension variation of classical and $p$-adic modular forms, Invent. Math. 133 (1998), 449–463.CrossRefGoogle Scholar
Wan, D., Xiao, L. and Zhang, J., Slopes of eigencurves over boundary disks, Math. Ann. 369 (2017), 487–537.CrossRefGoogle Scholar