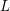 $L$-functions
$L$-functionsPublished online by Cambridge University Press: 30 May 2019
We prove that the complete 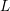 $L$-function associated to any cuspidal automorphic representation of
$L$-function associated to any cuspidal automorphic representation of 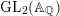 $\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$ has infinitely many simple zeros.
$\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$ has infinitely many simple zeros.
A. R. Booker was partially supported by EPSRC grant EP/K034383/1. P. J. Cho was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2016R1D1A1B03935186). No data were created in the course of this study.