Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T19:17:53.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Shifted generic cohomology

Part of: Representation theory of groups Linear algebraic groups and related topics Connections with homological algebra and category theory

Published online by Cambridge University Press:  07 August 2013

Brian J. Parshall ,
Leonard L. Scott  and
David I. Stewart
Brian J. Parshall
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22903, USA email [email protected]
Leonard L. Scott
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22903, USA email [email protected]
David I. Stewart
Affiliation:
New College, University of Oxford, Oxford OX1 3BN, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The idea that the cohomology of finite groups might be fruitfully approached via the cohomology of ambient semisimple algebraic groups was first shown to be viable in the papers [E. Cline, B. Parshall, and L. Scott, Cohomology of finite groups of Lie type, I, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 169–191] and [E. Cline, B. Parshall, L. Scott and W. van der Kallen, Rational and generic cohomology, Invent. Math. 39 (1977), 143–163]. The second paper introduced, through a limiting process, the notion of generic cohomology, as an intermediary between finite Chevalley group and algebraic group cohomology. The present paper shows that, for irreducible modules as coefficients, the limits can be eliminated in all but finitely many cases. These exceptional cases depend only on the root system and cohomological degree. In fact, we show that, for sufficiently large $r$, depending only on the root system and 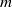$m$, and not on the prime 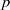$p$ or the irreducible module 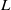$L$, there are isomorphisms 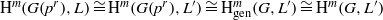${\mathrm{H} }^{m} (G({p}^{r} ), L)\cong {\mathrm{H} }^{m} (G({p}^{r} ), {L}^{\prime } )\cong { \mathrm{H} }_{\mathrm{gen} }^{m} (G, {L}^{\prime } )\cong {\mathrm{H} }^{m} (G, {L}^{\prime } )$, where the subscript ‘gen’ refers to generic cohomology and 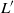${L}^{\prime } $ is a constructibly determined irreducible ‘shift’ of the (arbitrary) irreducible module 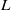$L$ for the finite Chevalley group 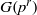$G({p}^{r} )$. By a famous theorem of Steinberg, both 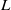$L$ and 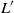${L}^{\prime } $ extend to irreducible modules for the ambient algebraic group 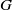$G$ with 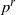${p}^{r} $-restricted highest weights. This leads to the notion of a module or weight being ‘shifted 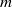$m$-generic’, and thus to the title of this paper. Our approach is based on questions raised by the third author in [D. I. Stewart, The second cohomology of simple 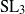${\mathrm{SL} }_{3} $-modules, Comm. Algebra 40 (2012), 4702–4716], which we answer here in the cohomology cases. We obtain many additional results, often with formulations in the more general context of 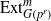${ \mathrm{Ext} }_{G({p}^{r} )}^{m} $ with irreducible coefficients.

Keywords

cohomology of finite groups of Lie typedefining characteristicbounding cohomologycomparison with algebraic group

MSC classification

Secondary: 20J06: Cohomology of groups 20G10: Cohomology theory 20C33: Representations of finite groups of Lie type 20C20: Modular representations and characters
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 10 , October 2013 , pp. 1765 - 1788
Copyright
© The Author(s) 2013 

References

Andersen, H., Extensions of modules for algebraic groups, Amer. J. Math. 106 (1984), 489–504.Google Scholar
Andersen, H., Jantzen, J. and Soergel, W., Representations of quantum groups at a pth root of unity and of semisimple groups in characteristic p, Astérisque 220 (1994).Google Scholar
Andersen, H., Jørgensen, J. and Landrock, P., The projective indecomposable modules of $\mathrm{SL} (2, {p}^{n} )$, Proc. Lond. Math. Soc. (3) 46 (1983), 38–52.Google Scholar
Bendel, C. P., Nakano, D. K., Parshall, B. J., Pillen, C., Scott, L. L. and Stewart, D. I., Bounding cohomology for finite groups and Frobenius kernels, Preprint (2012), arXiv:1208.6333.Google Scholar
Bendel, C., Nakano, D. and Pillen, C., On comparing the cohomology of algebraic groups, finite Chevalley groups and Frobenius kernels, J. Pure Appl. Algebra 163 (2001), 119–146.Google Scholar
Bendel, C., Nakano, D. and Pillen, C., Extensions for finite Chevalley groups. II, Trans. Amer. Math. Soc. 354 (2002), 4421–4454.Google Scholar
Bendel, C., Nakano, D. and Pillen, C., Extensions for finite Chevalley groups. I, Adv. Math. 183 (2004), 380–408.Google Scholar
Bendel, C., Nakano, D. and Pillen, C., Extensions for Frobenius kernels, J. Algebra 272 (2004), 476–511.Google Scholar
Bendel, C., Nakano, D. and Pillen, C., Extensions for finite groups of Lie type. II. Filtering the truncated induction functor, in Representations of algebraic groups, quantum groups, and Lie algebras, Contemporary Mathematics, vol. 413 (American Mathematical Society, Providence, RI, 2006), 1–23.Google Scholar
Bendel, C., Nakano, D. and Pilllen, C., On the vanishing ranges for the cohomology of finite groups of Lie type, Int. Math. Res. Not. IMRN (2011).Google Scholar
Bourbaki, N., Éléments de mathématique: groupes et algèbres de Lie (Masson, Paris, 1982), Chapters IV–VI.Google Scholar
Cline, E., Parshall, B. and Scott, L., Cohomology of finite groups of Lie type, I, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 169–191.CrossRefGoogle Scholar
Cline, E., Parshall, B. and Scott, L., Induced modules and affine quotients, Math. Ann. 230 (1977), 1–14.Google Scholar
Cline, E., Parshall, B. and Scott, L., Detecting rational cohomology, J. Lond. Math. Soc. (2) 28 (1983), 293–300.CrossRefGoogle Scholar
Cline, E., Parshall, B. and Scott, L., Abstract Kazhdan–Lusztig theories, Tohoku Math. J. (2) 45 (1993), 511–534.Google Scholar
Cline, E., Parshall, B. and Scott, L., Reduced standard modules and cohomology, Trans. Amer. Math. Soc. 361 (2009), 5223–5261.CrossRefGoogle Scholar
Cline, E., Parshall, B., Scott, L. and van der Kallen, W., Rational and generic cohomology, Invent. Math. 39 (1977), 143–163.Google Scholar
Franjou, V., Friedlander, E., Scorichenko, A. and Suslin, A., General linear and functor cohomology over finite fields, Ann. of Math. (2) 150 (1999), 663–728.Google Scholar
Friedlander, E. and Parshall, B., On the cohomology of algebraic and related finite groups, Invent. Math. 74 (1983), 85–117.CrossRefGoogle Scholar
Friedlander, E. and Parshall, B., Cohomology of infinitesimal and discrete groups, Math. Ann. 273 (1986), 353–374.Google Scholar
Jantzen, J., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003).Google Scholar
Koppinen, M., Good bimodule filtrations for coordinate rings, J. Lond. Math. Soc. (2) 30 (1984), 244–250.Google Scholar
Parshall, B. and Scott, L., Bounding Ext for modules for algebraic groups, finite groups and quantum groups, Adv. Math. 226 (2011), 2065–2088.CrossRefGoogle Scholar
Parshall, B. and Scott, L., New graded methods in the homological algebra of semisimple algebraic groups, Preprint (2013), arXiv:1304.1461.Google Scholar
Sin, P., Extensions of simple modules for special algebraic groups, J. Algebra 170 (1994), 1011–1034.Google Scholar
Stewart, D. I., The second cohomology of simple ${\mathrm{SL} }_{3} $-modules, Comm. Algebra 40 (2012), 4702–4716.Google Scholar
Stewart, D. I., Unbounding Ext, J. Algebra 365 (2012), 1–11.CrossRefGoogle Scholar
VIGRE Algebra Group, University of Georgia, Second cohomology for finite groups of Lie type, J. Algebra 360 (2012), 21–52, arXiv:1110.0228.Google Scholar